bzoj2956: 模积和（数论）

　　先算出无限制的情况，再减去i==j的情况。

　　无限制的情况很好算，有限制的情况需要将式子拆开。

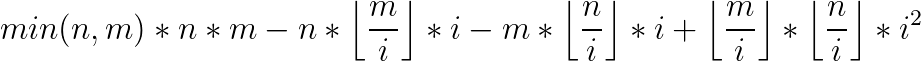
　　注意最后的地方要用平方和公式，模数+1是6的倍数，于是逆元就是（模数+1）/6

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#define MOD(x) ((x)>=mod?(x)-mod:(x))
using namespace std;
const int mod=,six=;
int n,m,sumn,summ,l1,r1,l2,r2,l,r;
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
int solve(int n,int m)
{
    int sum=;
    for(int i=;i<=n;i=r+)
    {
        l=m/(m/i+)+;r=m/(m/i);
        if(r>=n)r=n;
        sum=MOD(sum+(1ll*(m/i)*(r-l+)%mod*(l+r)%mod*((mod+)>>)%mod));
    }
    return sum;
}
int pfh(int n){return 1ll*n%mod*(n+)%mod*(*n+)%mod*six%mod;}
int main()
{
    read(n);read(m);
    sumn=(1ll*n*n-solve(n,n))%mod;summ=(1ll*m*m-solve(m,m))%mod;
    int sum=1ll*min(n,m)*n%mod*m%mod;
    for(int i=;i<=min(n,m);i=r+)
    {
        r=min(n/(n/i),m/(m/i));
        if(r>min(n,m))r=min(n,m);
        sum=MOD(sum+1ll*(n/i)*(m/i)%mod*MOD(pfh(r)+mod-pfh(i-))%mod);
    }
    sum=(sum+mod-(1ll*m*solve(min(n,m),n)%mod)+mod-(1ll*n*solve(min(n,m),m)%mod))%mod;
    printf("%lld\n",MOD(1ll*sumn*summ%mod+mod-sum));
}