BZOJ 1043 下落的圆盘

Description

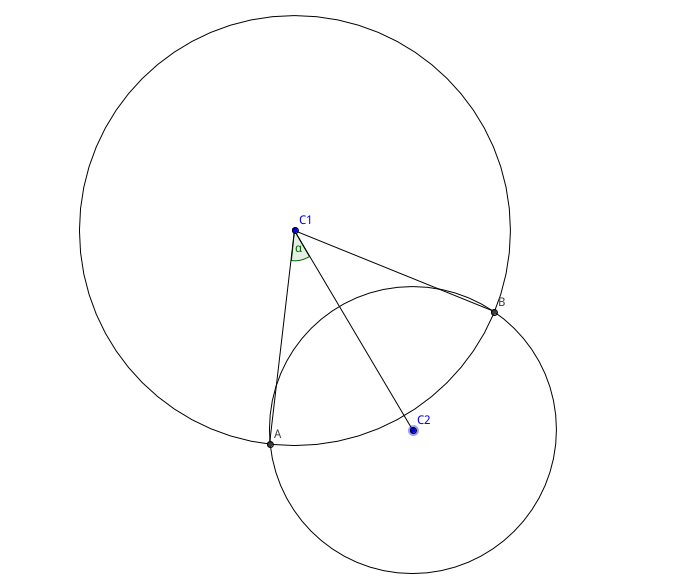
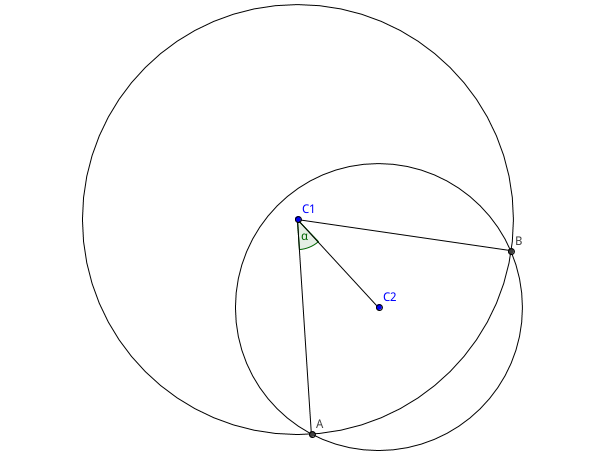
有n个圆盘从天而降，后面落下的可以盖住前面的。求最后形成的封闭区域的周长。看下面这副图, 所有的红色线条的总长度即为所求. 

Input

n ri xi y1 ... rn xn yn

Output

最后的周长，保留三位小数

Sample Input

2
1 0 0
1 1 0

Sample Output

10.472

HINT

数据规模

n<=1000

这道题目很好嘴巴，但是写起来有点儿蛋疼。

首先求出每个圆盘被他上面的圆盘覆盖的圆心角的度数α，用(2π-α)*c/2π即每个圆盘的周长答案，最后累加一遍答案即可。

那么圆心角要怎么求呢？？？

算出两个圆的交点肯定是没戏的(我推了很久的公式，还是退错了)，后面想想，好像不用去求交点，可以直接用圆心角来计算区间。

如图若两圆C1，C2有交点(C2覆盖C1)，则我们可以算出射线C1C2的极角θ。C1被C2所覆盖的圆心角的区间为[θ-α,θ+α]。但是注意，区间可能有越界的情况，比如说我们的区间是(-π,π]他的被覆盖的极角区间就是许多区间的并，但他可能和有[-1.2π，-0.7π]，这时我们需要将区间拆开进行处理。比如此例中，我们拆成[-π,-0.7π]与[0.8π,π]。

还有一种情况就是C1的圆心在C2中，α的值为其补角。(自己画画图)。

 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<cstdio>
 #include<cstdlib>
 using namespace std;

 #define pi (3.1415926535)
 #define esp (1e-6)
 #define maxn 2010
 int n; double ans;

 inline bool equal(double a,double b) { return fabs(a - b) < esp; }

 inline double qua(double a) { return a * a; } 

 inline bool dd(double a,double b) { if (equal(a,b)) return true; return a >= b; } //>=

 inline bool xd(double a,double b) { if (equal(a,b)) return true; return a <= b; } //<=

 struct NODE{ double x,y; };
 struct angle
 {
     double a1,a2;
     friend inline bool operator < (angle a,angle b)
     {
         if (!equal(a.a1,b.a1)) return xd(a.a1,b.a1);
         return xd(a.a2,b.a2);
     }
 }bac[maxn];
 struct CIR
 {
     double r,x,y;
     inline void read() { scanf("%lf %lf %lf",&r,&x,&y); }
     inline NODE mid() { return (NODE) {x,y}; }
     inline double calc(NODE p) { return atan2(p.y-y,p.x-x); }
     inline double C() { return *pi*r; }
 }cir[maxn];
 struct LINE
 {
     double a,b,c;
     inline double dis(NODE p) { return fabs(a*p.x+b*p.y+c)/sqrt(qua(a)+qua(b)); }
     inline double key(NODE p) { return p.x*a+p.y*b+c; }
 };

 inline double dis(NODE a,NODE b) { return sqrt(qua(a.x-b.x) + qua(a.y-b.y)); }

 inline bool have(CIR c1,CIR c2) { return dis(c1.mid(),c2.mid())<c1.r+c2.r; }

 inline bool cat(CIR c1,CIR c2) { return xd(dis(c1.mid(),c2.mid()),fabs(c1.r-c2.r)); }

 inline LINE cross(CIR c1,CIR c2) { return (LINE) {*(c2.x-c1.x),*(c2.y-c1.y),(qua(c2.r)-qua(c2.x)-qua(c2.y))-(qua(c1.r)-qua(c1.x)-qua(c1.y))}; }

 inline void work()
 {
     int tot,i,j; double rest,p,q,a,b,now; LINE l;
     for (i = n;i;--i)
     {
         tot = ; rest = ; now = ;
         for (j = i+;j <= n;++j)
         {
             if (cat(cir[i],cir[j]))
             {
                 if (cir[i].r > cir[j].r) continue;
                 else break;
             }
             if (have(cir[i],cir[j]))
             {
                 p = cir[i].calc(cir[j].mid()) + pi;
                 l = cross(cir[i],cir[j]);
                 q = l.dis(cir[i].mid());
                 q = acos(q/cir[i].r);
                 if (cir[i].r < cir[j].r&&l.key(cir[i].mid())*l.key(cir[j].mid()) > )
                     q = pi - q;
                 a = p - q; b = p + q;
                 if (dd(a,) && xd(b,*pi))
                     bac[++tot] = (angle) {a,b};
                 else if (a < )
                 {
                     bac[++tot] = (angle) {a+*pi,*pi};
                     bac[++tot] = (angle) {,b};
                 }
                 else
                 {
                     bac[++tot] = (angle) {a,*pi};
                     bac[++tot] = (angle) {,b-*pi};
                 }
             }
         }
         if (j != n+) continue;
         sort(bac+,bac+tot+);
         for (int j = ;j <= tot;++j)
         {
             if (bac[j].a1 > now)
             {
                 rest += bac[j].a1 - now;
                 now = bac[j].a2;
             }
             else now = max(now,bac[j].a2);
         }
         rest += *pi - now;
         ans += rest/(*pi) * cir[i].C();
     }
 }

 int main()
 {
     freopen("1043.in","r",stdin);
     freopen("1043.out","w",stdout);
     scanf("%d",&n);
     for (int i = ;i <= n;++i) cir[i].read();
     work();
     printf("%.3lf",ans);
     fclose(stdin); fclose(stdout);
     return ;
 }