Codeforces Round #432 (Div. 2, based on IndiaHacks Final Round 2017)ABCD

A. Arpa and a research in Mexican wave

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Arpa is researching the Mexican wave.

There are n spectators in the stadium, labeled from 1 to n. They start the Mexican wave at time 0.

• At time 1, the first spectator stands.
• At time 2, the second spectator stands.
• ...
• At time k, the k-th spectator stands.
• At time k + 1, the (k + 1)-th spectator stands and the first spectator sits.
• At time k + 2, the (k + 2)-th spectator stands and the second spectator sits.
• ...
• At time n, the n-th spectator stands and the (n - k)-th spectator sits.
• At time n + 1, the (n + 1 - k)-th spectator sits.
• ...
• At time n + k, the n-th spectator sits.

Arpa wants to know how many spectators are standing at time t.

Input

The first line contains three integers n, k, t (1 ≤ n ≤ 109, 1 ≤ k ≤ n, 1 ≤ t < n + k).

Output

Print single integer: how many spectators are standing at time t.

Examples

input

10 5 3

output

3

input

10 5 7

output

5

input

10 5 12

output

3

Note

In the following a sitting spectator is represented as -, a standing spectator is represented as ^.

• At t = 0  ----------  number of standing spectators = 0.
• At t = 1  ^---------  number of standing spectators = 1.
• At t = 2  ^^--------  number of standing spectators = 2.
• At t = 3  ^^^-------  number of standing spectators = 3.
• At t = 4  ^^^^------  number of standing spectators = 4.
• At t = 5  ^^^^^-----  number of standing spectators = 5.
• At t = 6  -^^^^^----  number of standing spectators = 5.
• At t = 7  --^^^^^---  number of standing spectators = 5.
• At t = 8  ---^^^^^--  number of standing spectators = 5.
• At t = 9  ----^^^^^-  number of standing spectators = 5.
• At t = 10 -----^^^^^  number of standing spectators = 5.
• At t = 11 ------^^^^  number of standing spectators = 4.
• At t = 12 -------^^^  number of standing spectators = 3.
• At t = 13 --------^^  number of standing spectators = 2.
• At t = 14 ---------^  number of standing spectators = 1.
• At t = 15 ----------  number of standing spectators = 0.

水题

#include<bits/stdc++.h>
#define pb push_back
#define ll long long
using namespace std;
const int maxn=1e2+;
int k,t,n;
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    cin>>n>>k>>t;
    if(t<=k)
    {
        cout<<t<<endl;
    }
    else if(t<=n)
    {
        cout<<k<<endl;
    }
    else
    {
        cout<<k-t+n<<endl;
    }

    return ;
} 

B. Arpa and an exam about geometry

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Arpa is taking a geometry exam. Here is the last problem of the exam.

You are given three points a, b, c.

Find a point and an angle such that if we rotate the page around the point by the angle, the new position of a is the same as the old position of b, and the new position of b is the same as the old position of c.

Arpa is doubting if the problem has a solution or not (i.e. if there exists a point and an angle satisfying the condition). Help Arpa determine if the question has a solution or not.

Input

The only line contains six integers ax, ay, bx, by, cx, cy (|ax|, |ay|, |bx|, |by|, |cx|, |cy| ≤ 109). It's guaranteed that the points are distinct.

Output

Print "Yes" if the problem has a solution, "No" otherwise.

You can print each letter in any case (upper or lower).

Examples

input

0 1 1 1 1 0

output

Yes

input

1 1 0 0 1000 1000

output

No

Note

In the first sample test, rotate the page around (0.5, 0.5) by .

In the second sample test, you can't find any solution.

题意：给三个不同的点a,b,c，问你是否可以找一个点d和角度v，把这三个点再围绕d转动v度使得，a在b原来的位置，b在原来的位置。

题解：只要三个点不在一条直线上并且ab==bc，就可以。注意求长度时开方会导致精度出错，所以不开方直接用整数表示。

#include<bits/stdc++.h>
#define pb push_back
#define ll long long
using namespace std;
const int maxn=1e2+;
const double inf=0x3f3f3f3f3f;
const double eps=1e-;
ll ax,ay,bx,by,cx,cy;
ll dis(ll x1,ll y1,ll x2,ll y2 )
{
    ll ans;
    ans=(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    cin>>ax>>ay>>bx>>by>>cx>>cy;
    ll tmp1=dis(ax,ay,bx,by);
    ll tmp2=dis(bx,by,cx,cy);
    double k1=abs(bx-ax)>?double(by-ay)/(bx-ax):inf;
    double k2=abs(cx-bx)>?double(cy-by)/(cx-bx):inf;
    if(k1==k2)
    {
        cout<<"NO"<<'\n';return ;
    }
    if(tmp1==tmp2)
    {
        cout<<"YES"<<'\n';
    }
    else
    {
        cout<<"NO"<<'\n';
    }
    return ;
} 

C. Five Dimensional Points

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.

We will call point a bad if there are different points b and c, not equal to a, from the given set such that angle between vectors 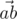 and 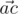 is acute (i.e. strictly less than 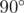). Otherwise, the point is called good.

The angle between vectors 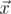 and 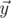 in 5-dimensional space is defined as 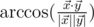, where  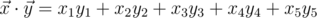is the scalar product and  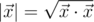is length of .

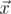Given the list of points, print the indices of the good points in ascending order.

Input

The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.

The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103)  — the coordinates of the i-th point. All points are distinct.

Output

First, print a single integer k — the number of good points.

Then, print k integers, each on their own line — the indices of the good points in ascending order.

Examples

input

6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

output

1
1

input

3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0

output

0

Note

In the first sample, the first point forms exactly a 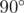 angle with all other pairs of points, so it is good.

In the second sample, along the cd plane, we can see the points look as follows:

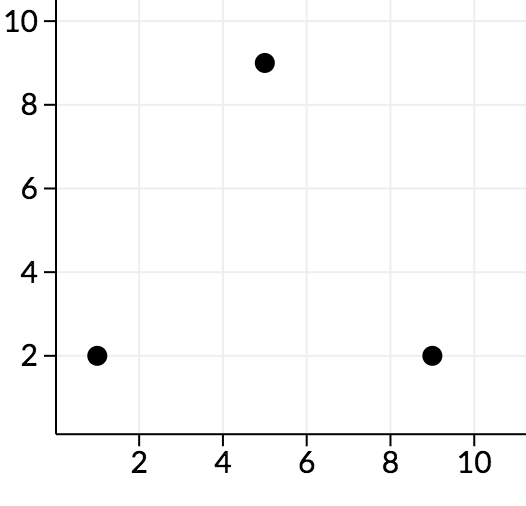
We can see that all angles here are acute, so no points are good.

题意：给你n个五维的点，一个点跟所有其他点构成的向量的角度都是钝角或直角的话则称这个点好。问给的点中有几个好点

题解：暴力判断每个点，（本来以为会被卡没想到过了）

#include<bits/stdc++.h>
#define pb push_back
#define ll long long
#define PI 3.14159265
using namespace std;
const int maxn=1e3+;
double a[maxn],b[maxn],c[maxn],d[maxn],e[maxn];
int ans[maxn],tmp,n;
struct node
{
    double a,b,c,d,e;
};
double dis(node t,node tt)
{
    return t.a*tt.a+t.b*tt.b+t.c*tt.c+t.d*tt.d+t.e*tt.e;
}
int slove(node x,node y)
{
    double sum=dis(x,y);
    double sum1=sqrt(dis(x,x))*sqrt(dis(y,y));
    return acos(sum/sum1)*180.0 / PI;
}
void s(int i)
{
        for(int j=;j<n;j++)
        {
            if(j==i)continue;
            for(int k=j+;k<=n;k++)
            {
                if(k==i)continue;
                node x,y;
                x.a=a[j]-a[i];y.a=a[k]-a[i];
                x.b=b[j]-b[i];y.b=b[k]-b[i];
                x.c=c[j]-c[i];y.c=c[k]-c[i];
                x.d=d[j]-d[i];y.d=d[k]-d[i];
                x.e=e[j]-e[i];y.e=e[k]-e[i];
                if(slove(x,y)<)
                {
                    return ;
                }
            }
        }
        ans[tmp++]=i;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    cin>>n;
    for(int i=;i<=n;i++)
    {
        cin>>a[i]>>b[i]>>c[i]>>d[i]>>e[i];
    }
    for(int i=;i<=n;i++)
    {
        s(i);
    }
    cout<<tmp<<endl;
    for(int i=;i<tmp;i++)
    {
        cout<<ans[i]<<endl;
    }

} 

D. Arpa and a list of numbers

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Arpa has found a list containing n numbers. He calls a list bad if and only if it is not empty and gcd (see notes section for more information) of numbers in the list is 1.

Arpa can perform two types of operations:

• Choose a number and delete it with cost x.
• Choose a number and increase it by 1 with cost y.

Arpa can apply these operations to as many numbers as he wishes, and he is allowed to apply the second operation arbitrarily many times on the same number.

Help Arpa to find the minimum possible cost to make the list good.

Input

First line contains three integers n, x and y (1 ≤ n ≤ 5·105, 1 ≤ x, y ≤ 109) — the number of elements in the list and the integers x and y.

Second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 106) — the elements of the list.

Output

Print a single integer: the minimum possible cost to make the list good.

Examples

input

4 23 17
1 17 17 16

output

40

input

10 6 2
100 49 71 73 66 96 8 60 41 63

output

10

Note

In example, number 1 must be deleted (with cost 23) and number 16 must increased by 1 (with cost 17).

A gcd (greatest common divisor) of a set of numbers is the maximum integer that divides all integers in the set. Read more about gcd here.

题意：给n个数，删除一个数花费x,把一个数加一花费y,问使得这n个数的gcd不为1的最小花费。

题解：用vis[]记录，每个数的出现次数，找到2~max(a[1~n])个数之间的所有质数，求出每个质数能把n个数整除的个数然后再根据这个排一下序，再用前面三个质数做为gcd，求出其中的最小值

#include<bits/stdc++.h>
#define pb push_back
#define ll long long
#define PI 3.14159265
using namespace std;
const int maxn=1e6+;
const ll inf=0xfffffffffffffff;
int a[maxn],n,x,y,maxt;
int vis[maxn];
bool prime[(int)1e6+];
vector<int>p;
bool cmp(int x,int y)
{
    return vis[x]!=vis[y]?vis[x]>vis[y]:x<y;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    cin>>n>>x>>y;
    for(int i=;i<=n;i++)
    cin>>a[i],vis[a[i]]++,maxt=max(maxt,a[i]);
    bool flag=false;
    if(maxt>)flag=true;
        for(int i=;i<=min(maxt,maxn-);i++)
    {
        if(!prime[i])
        {
            p.pb(i);
            for(int j=i*;j<=min(maxt,maxn-);j+=i)prime[j]=true,vis[i]+=vis[j];
        }
    }
    if(!flag)p.pb();
    sort(p.begin(),p.end(),cmp);
     ll ans=inf;
     for(int k=;k<min((int)p.size(),);k++)
     {
         ll sum=;
             for(int i=;i<=n;i++)
         {
             int t=a[i]%p[k];
             if(t)
             sum+=min((ll)x,(ll)(p[k]-t)*y);
          }
            ans=min(ans,sum);
     }
      cout<<ans<<endl;
}