使用Shader画常见的数学函数

使用Shader画常见的数学函数

本篇博文的灵感来自于Shader Books这一小节：https://thebookofshaders.com/05/?lan=ch

代码运行网站：http://editor.thebookofshaders.com/

一次函数

\[y = x + 0.5
\]

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

// Plot a line on Y using a value between 0.0-1.0
float plot(vec2 st, float y) {
    return smoothstep(y-0.01, y, st.y) - smoothstep(y, y+0.01, st.y);
}

void main() {
	vec2 st = gl_FragCoord.xy/u_resolution;

    float y = st.x + 0.5; // 这里对于每一个x，求出了其对应的y值；
    // Plot a line
    float pct = plot(st, y); //使用st
    // color = vec3(pct);
    vec3 color = pct*vec3(0.0,1.0,0.0);

	gl_FragColor = vec4(color,1.0);
}

代码整体比较抽象，但是仔细捋一下，也不算太复杂。

这个函数接收像素点对应的坐标，归一化之后的，以及其x对应的y值；由于这是一个shader，所以每个像素都会有一个对应的float返回值，我们尝试看一下每个像素对应的返回值的样子，并把它填充在网格里。

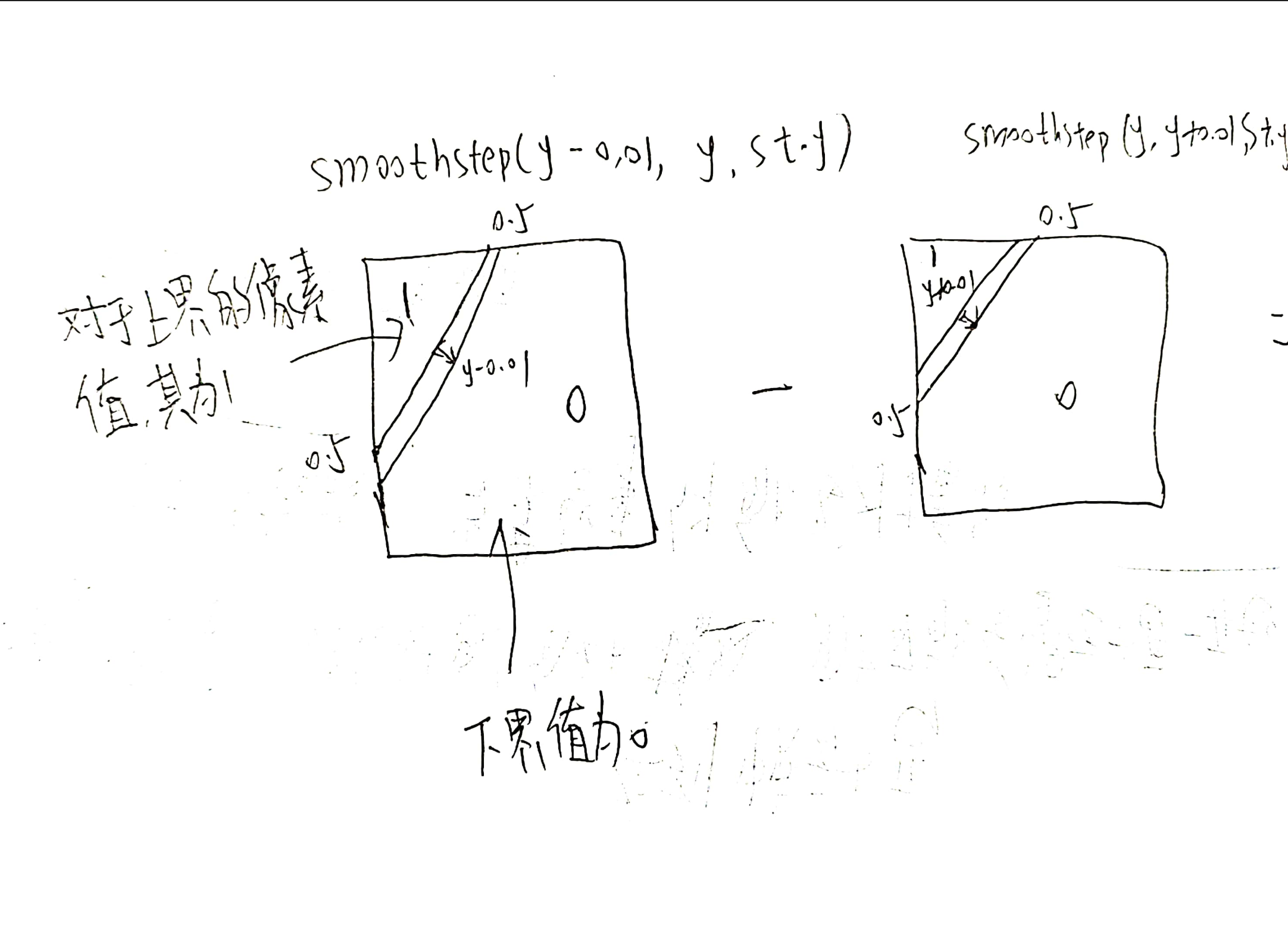
这样边根据y值得到了一条曲线。

二次函数

// Author: CuriosityWang
// Title: Expo

#ifdef GL_ES
precision mediump float;
#endif

#define PI 3.14159265359

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float plot(vec2 st, float y){
  return  smoothstep( y-0.01, y, st.y) -
          smoothstep( y, y+0.01, st.y);
}

void main() {
    vec2 st = gl_FragCoord.xy / u_resolution;

    float y = pow(st.x,	5.);

    float pct = plot(st, y);
 	vec3 color= pct*vec3(0.0,1.0,0.0);

    gl_FragColor = vec4(color,1.0);
}

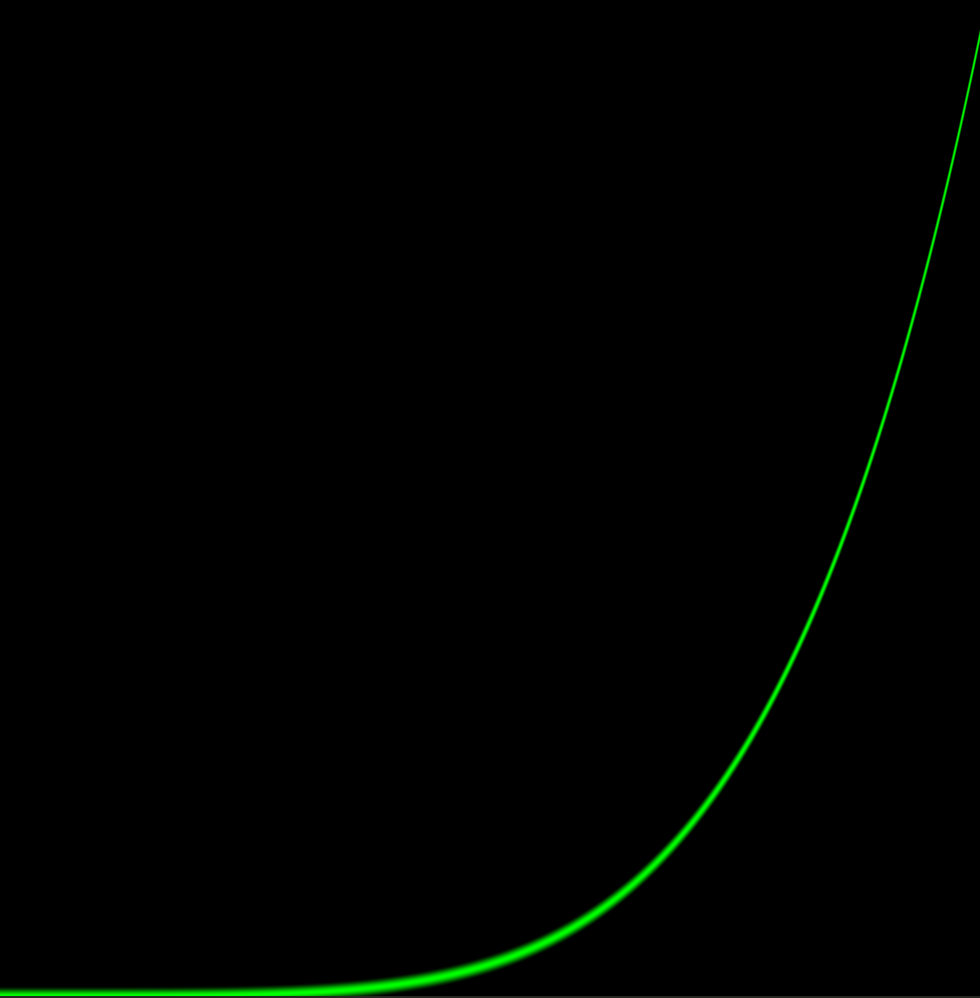
二次函数的实现道理是一样的，比较重要的点就是plot函数，根据smoothstep上界和下界，通过减法得到曲线。

三角函数

// Author: CuriosityWang
// Title: Expo

#ifdef GL_ES
precision mediump float;
#endif

#define PI 3.14159265359

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float plot(vec2 st, float y){
  return  smoothstep( y-0.01, y, st.y) -
          smoothstep( y, y+0.01, st.y);
}

void main() {
    vec2 st = gl_FragCoord.xy / u_resolution;

    float y = 0.5* sin(st.x*2.*PI) + 0.5;

    float pct = plot(st, y);
 	vec3 color= pct*vec3(0.0,1.0,0.0);

    gl_FragColor = vec4(color,1.0);
}

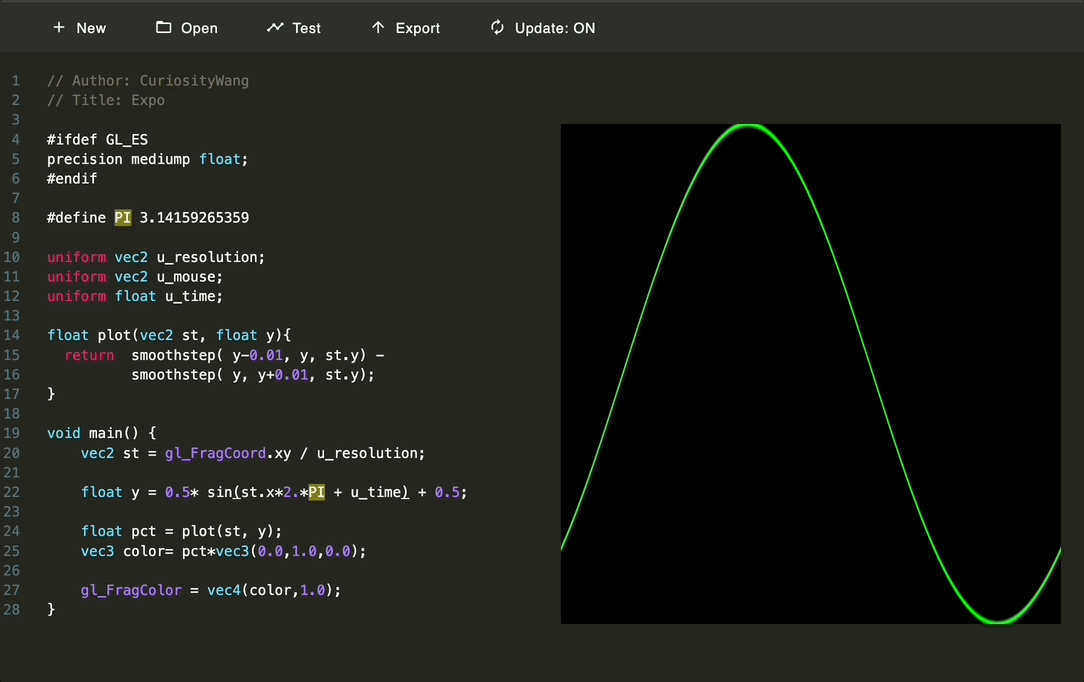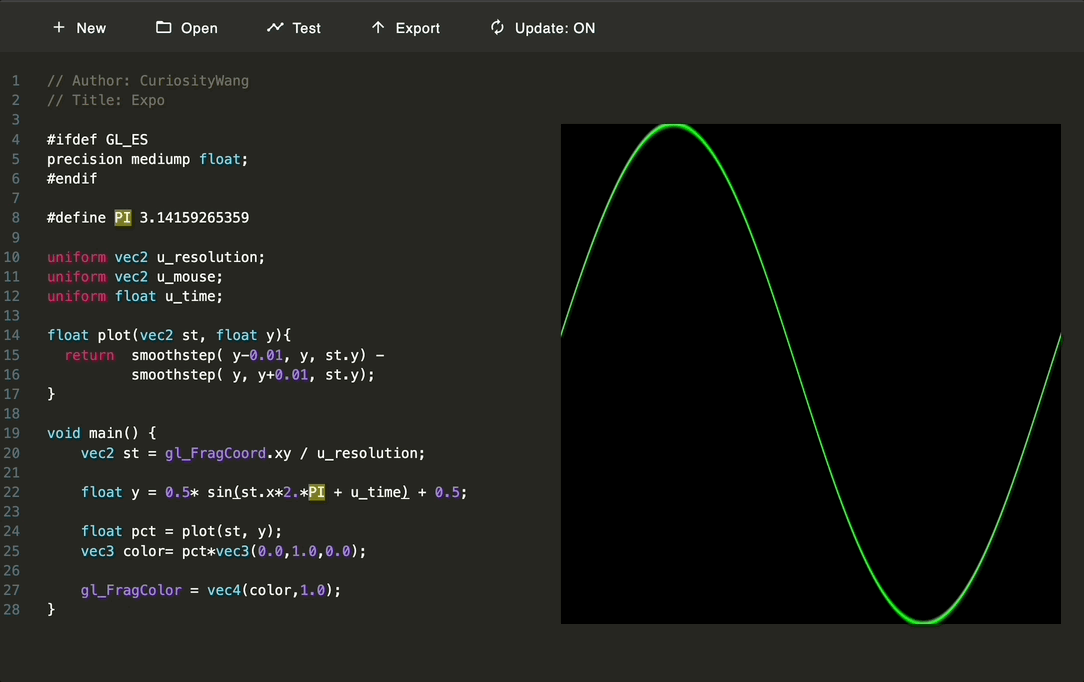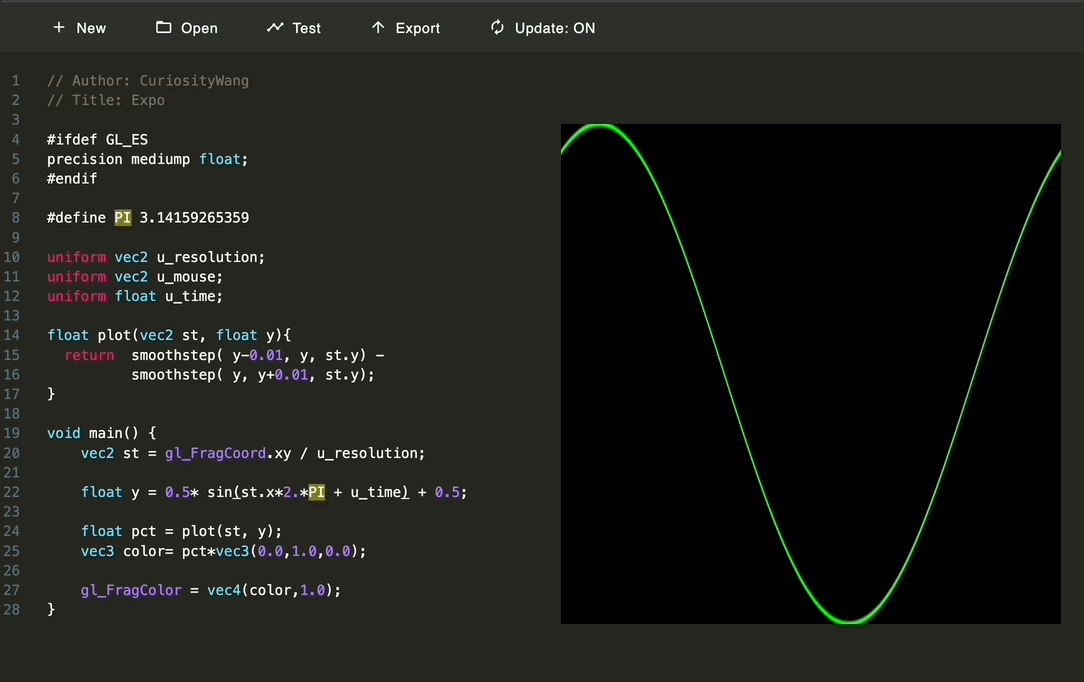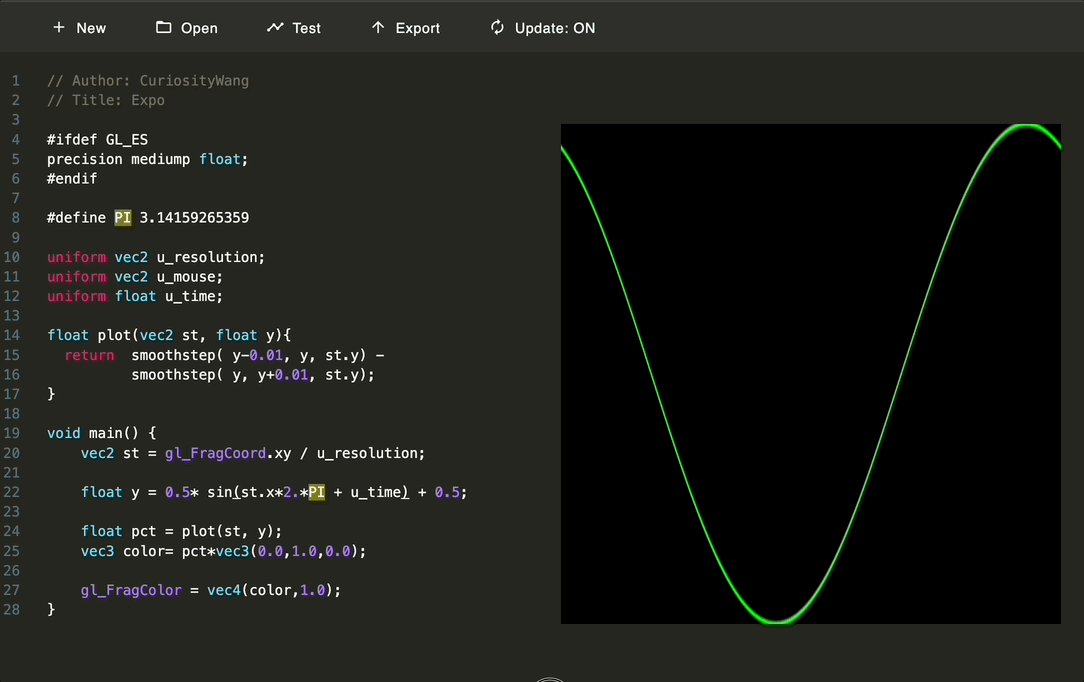
// Author: CuriosityWang
// Title: Expo

#ifdef GL_ES
precision mediump float;
#endif

#define PI 3.14159265359

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float plot(vec2 st, float y){
  return  smoothstep( y-0.01, y, st.y) -
          smoothstep( y, y+0.01, st.y);
}

void main() {
    vec2 st = gl_FragCoord.xy / u_resolution;

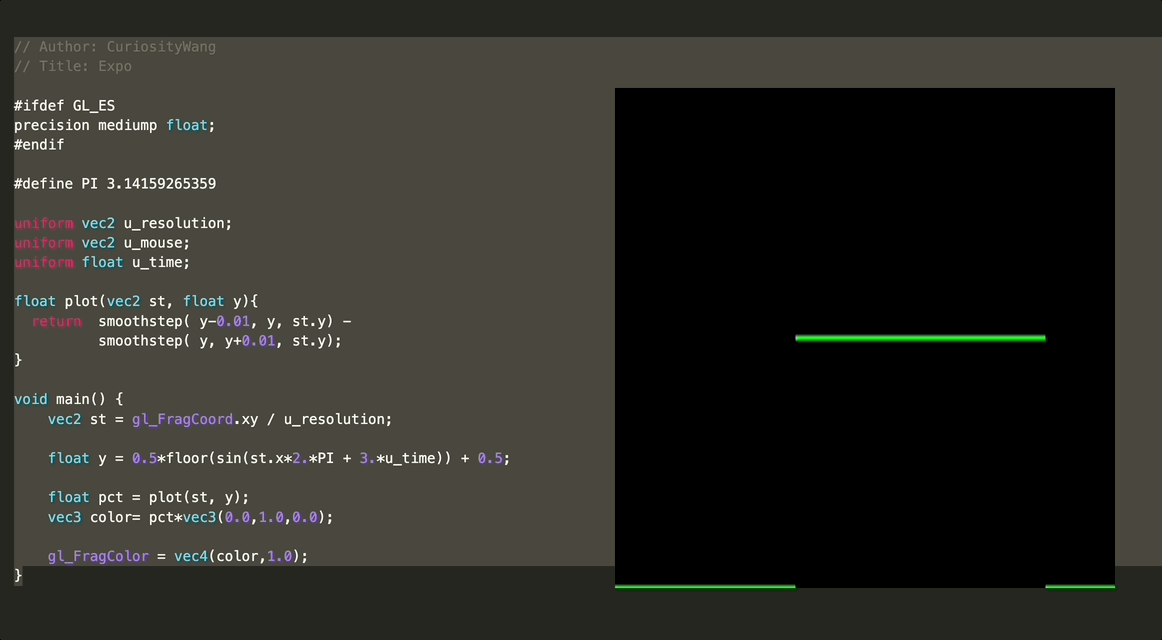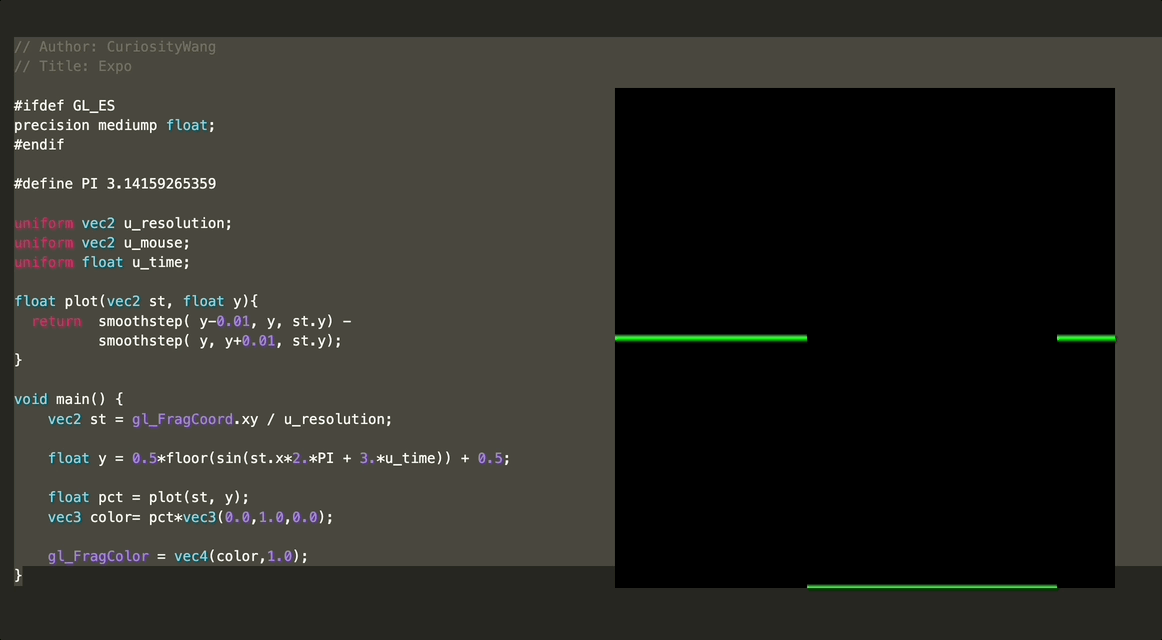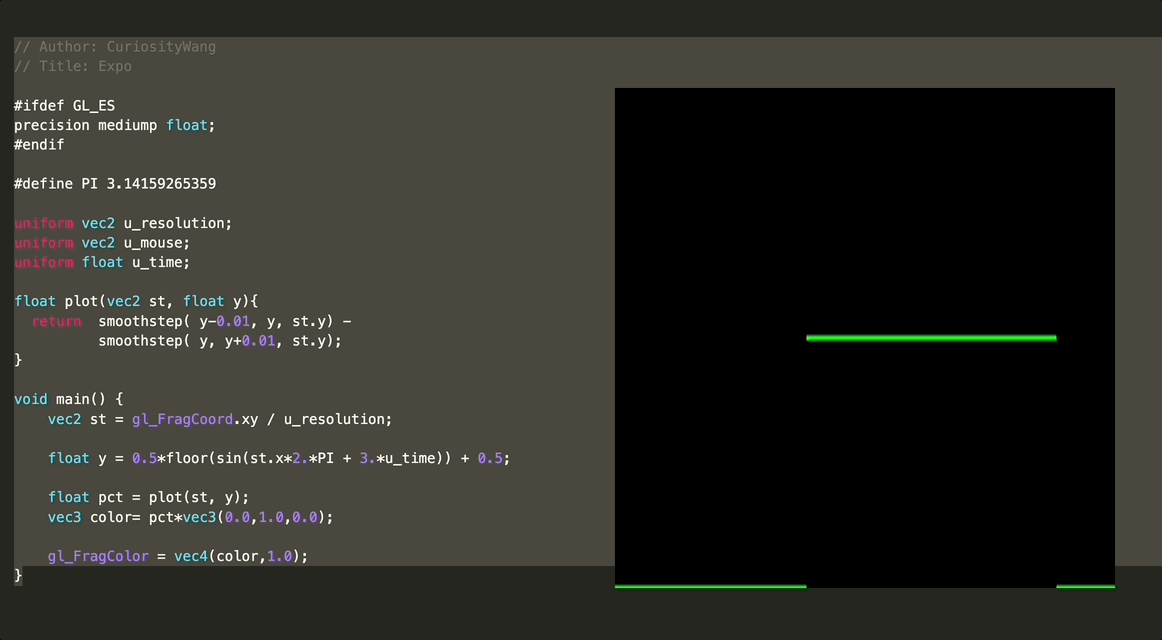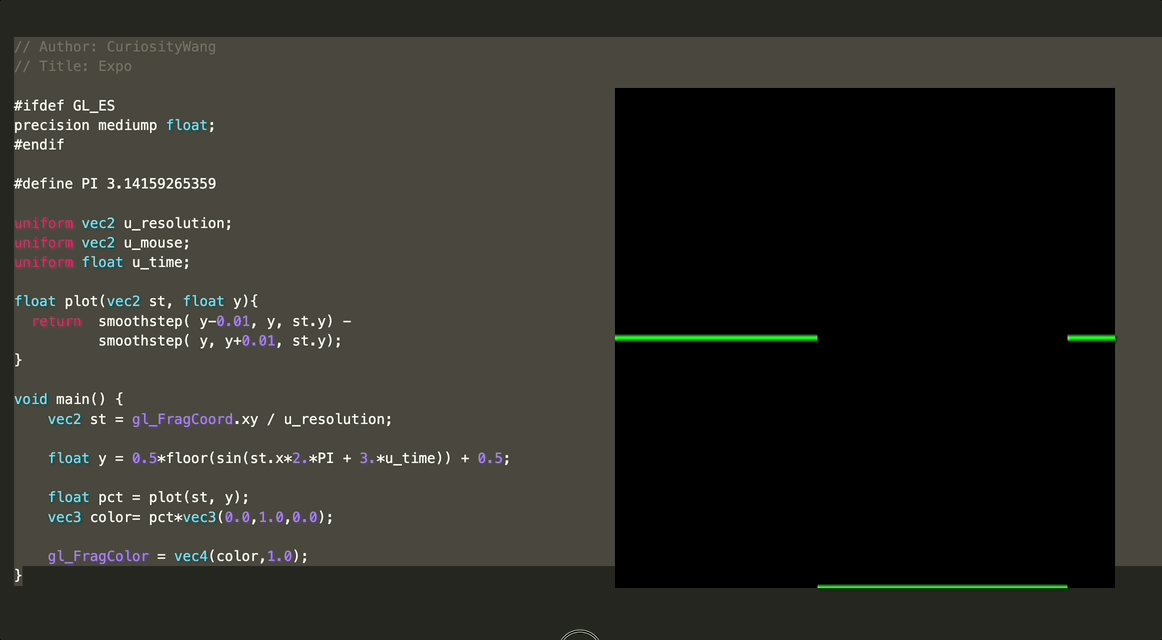
    float y = 0.5*floor(sin(st.x*2.*PI + 3.*u_time)) + 0.5;

    float pct = plot(st, y);
 	vec3 color= pct*vec3(0.0,1.0,0.0);

    gl_FragColor = vec4(color,1.0);
}