【Java】 大话数据结构(12) 查找算法(3) （平衡二叉树（AVL树））

本文根据《大话数据结构》一书及网络资料，实现了Java版的平衡二叉树（AVL树）。

平衡二叉树介绍

在上篇博客中所实现的二叉排序树（二叉搜索树），其查找性能取决于二叉排序树的形状，当二叉排序树比较平衡时（深度与完全二叉树相同，[log₂n]+1），时间复杂度为O(logn)；但也有可能出现极端的斜树，如依照{35,37,47,51,58,62,73,88,91,99}的顺序，构建的二叉排序树就如下图所示，查找时间复杂度为O(n)。

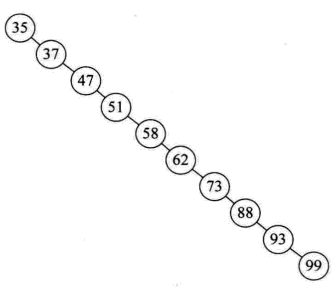
图1 斜树

为提高查找复杂度，在二叉排序树的基础上，提出了二叉平衡树：一种二叉排序树，其中每个结点的左右子树的高度差至多等于1。

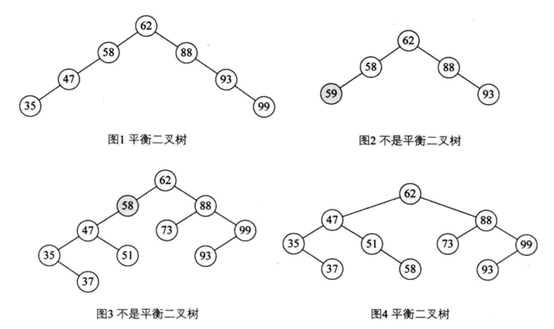
图2 平衡二叉树与非平衡二叉树

实现原理

定义二叉树结点的左子树深度减去右子树深度的值为平衡因子BF(Balance Factor)，平衡树所有结点的BF只能是-1，0，1。

距离新插入结点最近，且平衡因子的绝对值大于1的结点为根的子树，称为最小不平衡子树。

构建平衡二叉树的基本思想就是：在构建过程中，每当插入一个结点时，检查是否破坏了树的平衡性，若是，则找出最小不平衡树，进行相应的调整。

具体实现步骤很多地方都有介绍，本文不再赘述。

实现算法

二叉树的结点结构定义：

	private class AVLnode {
		int data; // 结点数据
		int bf; // 平衡因子,左高记为1，右高记为-1，平衡记为0
		AVLnode lChild, rChild; // 左右孩子

		public AVLnode(int data) {
			this.data = data;
			bf = 0;
			lChild = null;
			rChild = null;
		}
	}

　　

根据之前提到的基本思想，为调整最小不平衡树，首先要了解两种最基本的操作：左旋操作和右旋操作。

基本操作（左/右旋操作）

（1）右旋

如下图中左边的最小不平衡二叉树，进行右旋操作即可变为右边中的平衡二叉树。

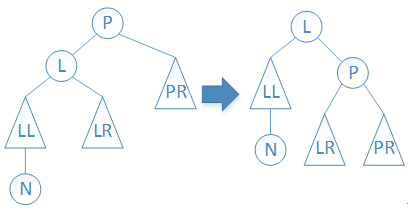
图3 右旋操作（情况1）

根据上图，容易编写右旋操作的代码如下：

	/*
	 * 右旋
	 * 返回新的根结点
	 */
	public AVLnode rRotate(AVLnode p) {
		AVLnode l = p.lChild;
		p.lChild = l.rChild;
		l.rChild = p;
		return l;
	}

　　

（2）左旋操作

同上所述，左旋操作的图示及代码，如下所示。

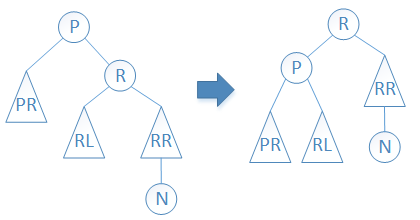
图4 左旋操作

	/*
	 * 左旋
	 * 返回新的根结点
	 */
	public AVLnode lRotate(AVLnode p) {
		AVLnode r = p.rChild;
		p.rChild = r.lChild;
		r.lChild = p;
		return r;
	}

　　

左/右平衡旋转

对于最小不平衡子树，若其左子树深度比右子树大2（下面称为左斜的不平衡树），需进行左平衡旋转操作。若右子树深度大，则需进行右平衡旋转操作。

（1）左平衡旋转：

左斜的不平衡树有几种形式，下面分开讨论

>> L结点的BF值为1时

　　直接对根结点P右旋即可

　　情况(1)：如下图所示，右旋根结点P。平衡后，P结点的BF值为0，其左结点L的BF值也为0。

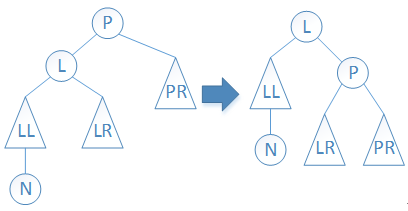
图5 情况(1)

>> L结点的BF值为-1时

　　都是先对L结点左旋，再对P结点右旋。根据平衡后P结点和L结点的BF值不同，可以分出下面三种情况：

　　情况(2)：如下图所示，先左旋L结点，再右旋P结点。平衡后，P结点的BF值为-1，L结点的BF值为0，LR结点的BF值为0。

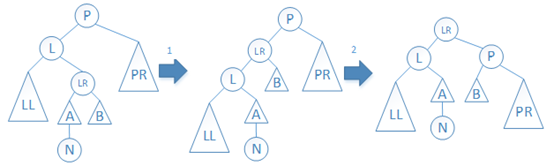
图6 情况(2)

（注：示意图中，小三角形表示的子树比大三角形表示的子树深度少1，下同）

　　情况(3)：如下图所示，先左旋L结点，再右旋P结点。平衡后，P结点的BF值为0，L结点的BF值为1，LR结点的BF值为0。

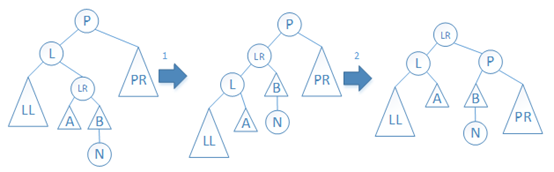
图7 情况(3)

　　情况(4)：如下图所示，先左旋L结点，再右旋P结点。平衡后，P结点的BF值为0，L结点的BF值为0，LR结点的BF值为0。

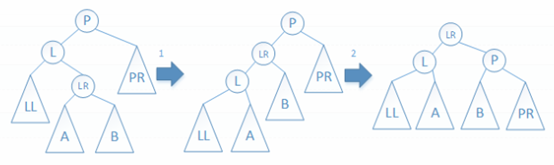
图8 情况(4)

>> L结点的BF值为0时

　　最小不平衡子树也可能出现下面这种情况（插入时不会出现，但删除操作过程中可能出现），《大话》一书中没有讨论到这种情况。

　　情况(5)：如下图所示，直接右旋P结点。平衡后，L结点的BF值为-1，LR结点的BF值为1。

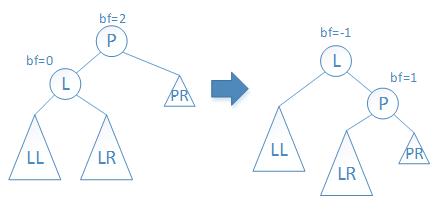
图9 情况(5)

综上所述，左平衡旋转一共可能出现5种情况，以下为左平衡旋转操作的代码：

	/*
	 * 左平衡旋转(左子树高度比右子树高2时(左斜)执行的操作)
	 * 返回值为新的根结点
	 */
	public AVLnode leftBalance(AVLnode p) {
		AVLnode l = p.lChild;
		switch (l.bf) {
		case 1: // 情況(1)
			p.bf = 0;
			l.bf = 0;
			return rRotate(p);
		case -1:
			AVLnode lr = l.rChild;
			switch (lr.bf) {
			case 1: // 情況(2)
				p.bf = -1;
				l.bf = 0;
				break; // break别漏写了
			case -1: // 情況(3)
				p.bf = 0;
				l.bf = 1;
				break;
			case 0: // 情況(4)
				p.bf = 0;
				l.bf = 0;
				break;
			}
			lr.bf = 0;
			// 设置好平衡因子bf后，先左旋
			p.lChild = lRotate(l);// 不能用l=leftBalance(l);
			// 再右旋
			return rRotate(p);
		case 0: // 这种情况书中没有考虑到，情况(5)
			l.bf = -1;
			p.bf = 1;
			return rRotate(p);
		}
		// 以下情况应该是不会出现的，所有情况都已经包括，除非程序还有问题
		System.out.println("bf超出范围，请检查程序！");
		return p;
	}

　　

（2）右平衡旋转：

　　与左平衡的分析类似，也可以分为五种情况，不再赘述，下面直接给出代码：

	/*
	 * 右平衡旋转(右子树高度比左子树高2时执行的操作)
	 * 返回值为新的根结点
	 */
	public AVLnode rightBalance(AVLnode p) {
		AVLnode r = p.rChild;
		switch (r.bf) {
		case -1:
			p.bf = 0;
			r.bf = 0;
			return lRotate(p);
		case 1:
			AVLnode rl = r.lChild;
			switch (rl.bf) {
			case 1:
				r.bf = -1;
				p.bf = 0;
				break;
			case -1:
				r.bf = 0;
				p.bf = 1;
				break;
			case 0:
				r.bf = 0;
				p.bf = 0;
				break;
			}
			rl.bf = 0;
			p.rChild = rRotate(r);
			return lRotate(p);
		case 0:
			p.bf = -1;
			r.bf = 1;
			return lRotate(p);
		}
		// 以下情况应该是不会出现的，所有情况都已经包括，除非程序还有问题
		System.out.println("bf超出范围，请检查程序！");
		return p;
	}

　　

插入操作的主函数

二叉平衡树是一种二叉排序树，所以其操作与二叉排序树相同，但为了保持平衡，需要对平衡度进行分析。

引入一个变量taller来衡量子树是否长高，若子树长高了，就必须对平衡度进行分析：如果不平衡，就进行上面所说的左右平衡旋转操作。

具体的Java实现代码如下：

	/*
	 * 插入操作
	 * 要多定义一个taller变量
	 */
	boolean taller;// 树是否长高

	public void insert(int key) {
		root = insert(root, key);
	}

	private AVLnode insert(AVLnode tree, int key) {// 二叉查找树的插入操作一样，但多了树是否长高的判断（树没长高就完全类似BST二叉树），要记得每次对taller赋值
		if (tree == null) {
			taller = true;
			return new AVLnode(key);
		}
		if (key == tree.data) {
			System.out.println("数据重复，无法插入！");
			taller = false;
			return tree;
		} else if (key < tree.data) {
			tree.lChild = insert(tree.lChild, key);
			if (taller == true) { // 左子树长高了，要对tree的平衡度分析
				switch (tree.bf) {
				case 1: // 原本左子树比右子树高，需要左平衡处理
					taller = false; // 左平衡处理，高度没有增加
					return leftBalance(tree);
				case 0: // 原本左右子树等高，现因左子树增高而增高
					tree.bf = 1;
					taller = true;
					return tree;
				case -1: // 原本右子树比左子树高，现左右子树相等
					tree.bf = 0;
					taller = false;
					return tree;
				}
			}
		} else if (key > tree.data) {
			tree.rChild = insert(tree.rChild, key);
			if (taller == true) { // 右子树长高了，要对tree的平衡度分析
				switch (tree.bf) {
				case 1: // 原本左子树高，现等高
					tree.bf = 0;
					taller = false;
					return tree;
				case 0: // 原本等高，现右边增高了
					tree.bf = -1;
					taller = true;
					return tree;
				case -1: // 原本右子树高，需右平衡处理
					taller = false;
					return rightBalance(tree);
				}
			}
		}
		return tree;
	}

　　

AVL树的完整代码

AVL树的完整代码如下（含测试代码）：

package AVLTree;

/**
 * AVL树
 * @author Yongh
 *
 */
public class AVLTree {

	private AVLnode root;

	private class AVLnode {
		int data; // 结点数据
		int bf; // 平衡因子,左高记为1，右高记为-1，平衡记为0
		AVLnode lChild, rChild; // 左右孩子

		public AVLnode(int data) {
			this.data = data;
			bf = 0;
			lChild = null;
			rChild = null;
		}
	}

	/*
	 * 右旋
	 * 返回新的根结点
	 */
	public AVLnode rRotate(AVLnode p) {
		AVLnode l = p.lChild;
		p.lChild = l.rChild;
		l.rChild = p;
		return l;
	}

	/*
	 * 左旋
	 * 返回新的根结点
	 */
	public AVLnode lRotate(AVLnode p) {
		AVLnode r = p.rChild;
		p.rChild = r.lChild;
		r.lChild = p;
		return r;
	}

	/*
	 * 左平衡旋转(左子树高度比右子树高2时(左斜)执行的操作)
	 * 返回值为新的根结点
	 */
	public AVLnode leftBalance(AVLnode p) {
		AVLnode l = p.lChild;
		switch (l.bf) {
		case 1: // 情況(1)
			p.bf = 0;
			l.bf = 0;
			return rRotate(p);
		case -1:
			AVLnode lr = l.rChild;
			switch (lr.bf) {
			case 1: // 情況(2)
				p.bf = -1;
				l.bf = 0;
				break; // break别漏写了
			case -1: // 情況(3)
				p.bf = 0;
				l.bf = 1;
				break;
			case 0: // 情況(4)
				p.bf = 0;
				l.bf = 0;
				break;
			}
			lr.bf = 0;
			// 设置好平衡因子bf后，先左旋
			p.lChild = lRotate(l);// 不能用l=leftBalance(l);
			// 再右旋
			return rRotate(p);
		case 0: // 这种情况书中没有考虑到，情况(5)
			l.bf = -1;
			p.bf = 1;
			return rRotate(p);
		}
		// 以下情况应该是不会出现的，所有情况都已经包括，除非程序还有问题
		System.out.println("bf超出范围，请检查程序！");
		return p;
	}

	/*
	 * 右平衡旋转(右子树高度比左子树高2时执行的操作)
	 * 返回值为新的根结点
	 */
	public AVLnode rightBalance(AVLnode p) {
		AVLnode r = p.rChild;
		switch (r.bf) {
		case -1:
			p.bf = 0;
			r.bf = 0;
			return lRotate(p);
		case 1:
			AVLnode rl = r.lChild;
			switch (rl.bf) {
			case 1:
				r.bf = -1;
				p.bf = 0;
				break;
			case -1:
				r.bf = 0;
				p.bf = 1;
				break;
			case 0:
				r.bf = 0;
				p.bf = 0;
				break;
			}
			rl.bf = 0;
			p.rChild = rRotate(r);
			return lRotate(p);
		case 0:
			p.bf = -1;
			r.bf = 1;
			return lRotate(p);
		}
		// 以下情况应该是不会出现的，所有情况都已经包括，除非程序还有问题
		System.out.println("bf超出范围，请检查程序！");
		return p;
	}

	/*
	 * 插入操作
	 * 要多定义一个taller变量
	 */
	boolean taller;// 树是否长高

	public void insert(int key) {
		root = insert(root, key);
	}

	private AVLnode insert(AVLnode tree, int key) {// 二叉查找树的插入操作一样，但多了树是否长高的判断（树没长高就完全类似BST二叉树），要记得每次对taller赋值
		if (tree == null) {
			taller = true;
			return new AVLnode(key);
		}
		if (key == tree.data) {
			System.out.println("数据重复，无法插入！");
			taller = false;
			return tree;
		} else if (key < tree.data) {
			tree.lChild = insert(tree.lChild, key);
			if (taller == true) { // 左子树长高了，要对tree的平衡度分析
				switch (tree.bf) {
				case 1: // 原本左子树比右子树高，需要左平衡处理
					taller = false; // 左平衡处理，高度没有增加
					return leftBalance(tree);
				case 0: // 原本左右子树等高，现因左子树增高而增高
					tree.bf = 1;
					taller = true;
					return tree;
				case -1: // 原本右子树比左子树高，现左右子树相等
					tree.bf = 0;
					taller = false;
					return tree;
				}
			}
		} else if (key > tree.data) {
			tree.rChild = insert(tree.rChild, key);
			if (taller == true) { // 右子树长高了，要对tree的平衡度分析
				switch (tree.bf) {
				case 1: // 原本左子树高，现等高
					tree.bf = 0;
					taller = false;
					return tree;
				case 0: // 原本等高，现右边增高了
					tree.bf = -1;
					taller = true;
					return tree;
				case -1: // 原本右子树高，需右平衡处理
					taller = false;
					return rightBalance(tree);
				}
			}
		}
		return tree;
	}

	/*
	 * 前序遍历
	 */
	public void preOrder() {
		preOrderTraverse(root);
		System.out.println();
	}

	private void preOrderTraverse(AVLnode node) {
		if (node == null)
			return;
		System.out.print(node.data+" ");
		preOrderTraverse(node.lChild);
		preOrderTraverse(node.rChild);
	}

	/*
	 * 中序遍历
	 */
	public void inOrder() {
		inOrderTraverse(root);
		System.out.println();
	}

	private void inOrderTraverse(AVLnode node) {
		if (node == null)
			return;
		inOrderTraverse(node.lChild);
		System.out.print(node.data+" ");
		inOrderTraverse(node.rChild);
	}

	/*
	 * 测试代码
	 */
	public static void main(String[] args) {
		AVLTree aTree = new AVLTree();
		int[] arr = { 3, 2, 1, 4, 5, 6, 7, 10, 9, 8 };
		for (int i : arr) {
			aTree.insert(i);
		}
		System.out.print("前序遍历结果：");
		aTree.preOrder();
		System.out.print("中序遍历结果：");
		aTree.inOrder();

		AVLTree bTree = new AVLTree();
		int[] arr2 = { 3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9 };
		for (int i : arr2) {
			bTree.insert(i);
		}
		System.out.print("前序遍历结果：");
		bTree.preOrder();
		System.out.print("中序遍历结果：");
		bTree.inOrder();
	}

}

　　

前序遍历结果：
中序遍历结果：
前序遍历结果：
中序遍历结果：                

AVLTree

测试代码中的两个AVL树如下图所示：

　　

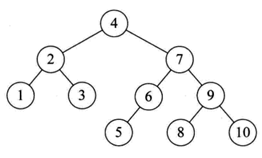
图10 aTree

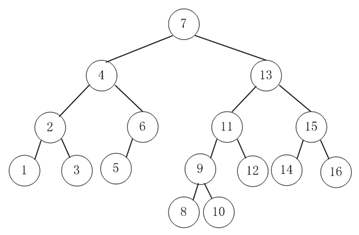
图11 bTree

后记

　　如果不用平衡因子BF，而是子树的高度来进行分析，讨论的情况就比较少，可参考这篇博客：AVL树(三)之 Java的实现