洛谷 P2146 [NOI2015]软件包管理器 解题报告

P2146 [NOI2015]软件包管理器

题目描述

Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。Debian/Ubuntu使用的apt-get，Fedora/CentOS使用的yum，以及OSX下可用的homebrew都是优秀的软件包管理器。

你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包A依赖软件包B，那么安装软件包A以前，必须先安装软件包B。同时，如果想要卸载软件包B，则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除0号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而0号软件包不依赖任何一个软件包。依赖关系不存在环（若有m(m≥2)个软件包A1,A2,A3,⋯,Am，其中A1依赖A2，A2依赖A3，A3依赖A4，……，A[m-1]依赖Am，而Am依赖A1，则称这m个软件包的依赖关系构成环），当然也不会有一个软件包依赖自己。

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为0。

输入输出格式

输入格式：

输入文件的第1行包含1个整数n，表示软件包的总数。软件包从0开始编号。

随后一行包含n−1个整数，相邻整数之间用单个空格隔开，分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。

接下来一行包含1个整数q，表示询问的总数。之后q行，每行1个询问。询问分为两种：

install x：表示安装软件包x

uninstall x：表示卸载软件包x

你需要维护每个软件包的安装状态，一开始所有的软件包都处于未安装状态。

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

输出文件

第i行输出1个整数，为第i步操作中改变安装状态的软件包数。

数据范围：

---

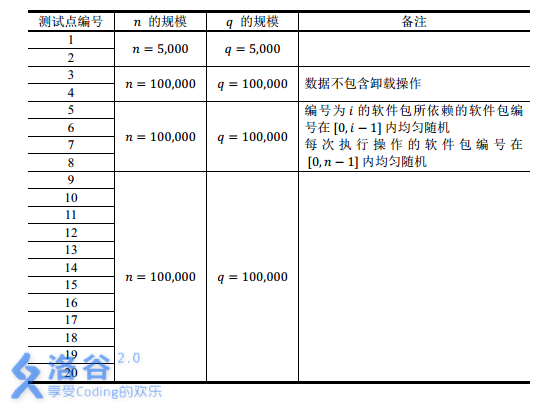
虽说是树剖裸题，但感觉我今天好幸运。

改变了一个写线段树的习惯

以往我写线段树时，\(lazy[i]\)代表节点\(i\)待更新，而普通的区间修改也是不根据它的儿子去更新。

所以在这个题里，将链改成某一个值时，我想了好久\(lazy\)怎么打，最后发现如果用儿子（也只能这样）去更新得先下发它，有点麻烦。

于是决定改掉这个局限性比较大的做法，以后\(lazy\)即代表它儿子欠更新，方便了很多，而不管维护什么信息，都可以通过儿子更新。

---

Code:

#include <cstdio>
#include <cstring>
#define ls id<<1
#define rs id<<1|1
int min(int x,int y){return x<y?x:y;}
int max(int x,int y){return x>y?x:y;}
const int N=100010;
int head[N],to[N],next[N],cnt;
void add(int u,int v)
{
    to[++cnt]=v;next[cnt]=head[u];head[u]=cnt;
}
int ws[N],dfn[N],siz[N],dep[N],top[N],f[N],time,n,m;
void dfs1(int now)
{
    siz[now]++;
    for(int i=head[now];i;i=next[i])
    {
        int v=to[i];
        dep[v]=dep[now]+1;
        dfs1(v);
        siz[now]+=siz[v];
        if(siz[ws[now]]<siz[v])
            ws[now]=v;
    }
}
void dfs2(int now,int anc)
{
    dfn[now]=++time;
    top[now]=anc;
    if(!ws[now]) return;
    dfs2(ws[now],anc);
    for(int i=head[now];i;i=next[i])
        if(!dfn[to[i]])
            dfs2(to[i],to[i]);
}
int dat[N<<2],lazy[N<<2];
void push_down(int id,int l,int r)
{
    if(l!=r)
    {
        int mid=l+r>>1;
        dat[ls]=lazy[id]*(mid+1-l);
        dat[rs]=lazy[id]*(r-mid);
        lazy[ls]=lazy[id],lazy[rs]=lazy[id];
    }
    lazy[id]=-1;
}
void change(int id,int L,int R,int l,int r,int delta)
{
    if(lazy[id]!=-1) push_down(id,L,R);
    if(L==l&&r==R) {lazy[id]=delta;dat[id]=delta*(r+1-l);return;}
    int mid=L+R>>1;
    if(r<=mid) change(ls,L,mid,l,r,delta);
    else if(l>mid) change(rs,mid+1,R,l,r,delta);
    else change(ls,L,mid,l,mid,delta),change(rs,mid+1,R,mid+1,r,delta);
    dat[id]=dat[ls]+dat[rs];
}
int query(int id,int L,int R,int l,int r)
{
    if(L==l&&R==r) return dat[id];
    if(lazy[id]!=-1) push_down(id,L,R);
    int mid=L+R>>1;
    if(r<=mid) return query(ls,L,mid,l,r);
    else if(l>mid) return query(rs,mid+1,R,l,r);
    else return query(ls,L,mid,l,mid)+query(rs,mid+1,R,mid+1,r);
}
int t_query(int x,int y)
{
    int ans=0;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]>dep[top[y]])
        {
            ans+=query(1,1,n,dfn[top[x]],dfn[x]);
            x=f[top[x]];
        }
        else
        {
            ans+=query(1,1,n,dfn[top[y]],dfn[y]);
            y=f[top[y]];
        }
    }
    ans+=query(1,1,n,min(dfn[x],dfn[y]),max(dfn[x],dfn[y]));
    return ans;
}
void t_change(int x,int y,int typ)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]>dep[top[y]])
        {
            change(1,1,n,dfn[top[x]],dfn[x],typ);
            x=f[top[x]];
        }
        else
        {
            change(1,1,n,dfn[top[y]],dfn[y],typ);
            y=f[top[y]];
        }
    }
    change(1,1,n,min(dfn[x],dfn[y]),max(dfn[x],dfn[y]),typ);
}
int main()
{
    scanf("%d",&n);
    int fa,x;char c[15];
    for(int i=2;i<=n;i++)
    {
        scanf("%d",&fa);
        add(fa+1,i);
        f[i]=fa+1;
    }
    dep[1]=1;
    dfs1(1);dfs2(1,1);
    scanf("%d",&m);
    memset(lazy,-1,sizeof(lazy));
    for(int i=1;i<=m;i++)
    {
        scanf("%s%d",c,&x);
        x++;
        if(c[0]=='i')
        {
            printf("%d\n",dep[x]-t_query(1,x));
            t_change(1,x,1);
        }
        else
        {
            printf("%d\n",query(1,1,n,dfn[x],dfn[x]+siz[x]-1));
            change(1,1,n,dfn[x],dfn[x]+siz[x]-1,0);
        }
    }
    return 0;
}

---

2018.6.29