KMP字符串匹配 简单理解

http://www.cnblogs.com/c-cloud/p/3224788.html

字符串匹配，长串长度为m,子串长度为n

则，暴力破解的复杂度为o(m*n)

如果用kmp匹配，则复杂度为o(m+n)

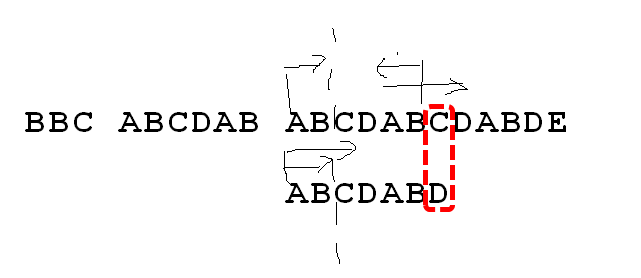
例如： 当上面的长串遍历到C时，与子串未匹配上失败，如果从头再来则上面子串是从B开始，子串从A开始；效率实在太低。

由图可知，前面已经有6个元素完全匹配上；而这6个元素本身的  部分匹配值位2，也就是从左往右；从右往左共同的子串，长度为2。既然6个元素+C无法与子串匹配上；

那么退而求其次，(长串中)是否右边小子串(公共串)+C,与子串从左往右公共串+1的元素匹配上呢？那么也就是，子串从C的位置开始，长串匹配位置不动，有效提高了速度。继续下去，就找到了长串。

部分匹配表

以首字母为开头

长度为

1

2

3

...

len

不同固定长度下的，(每个固定长度都有1个取值)

前缀和后缀的最长的共有元素的长度

前缀不能到底，后缀不能到开头

q = 1;

q = 2;

q = 3;

......

　　

#include<stdio.h>

最原始求解next的方法

int next[30] = {0};
int flag;

int get_2_next(char *p, int current, int flag1) //P为所求的字符串，current为当前的位置，flag1为函数中的移动标志位
{
        int i,j;
        char p1[30];
        char p2[30];                             //临时数组，便于比较

        if(current == 0)
                next[0] = 0;                     //因为位置为0的时候，既没有前缀，也没有后缀
        while(flag1 <= current)//flag1=1，从最长的长度开始
        {
                for(i = 0; i <= current - flag1; i++)//从首开始
                {
                        p1[i] = p[i];
                }
                p1[i] = '\0';

                for(i = flag1; i <= current; i++)//从尾开始
                {
                        p2[i - flag1] = p[i];
                }
                p2[i - flag1] = '\0';

                if(strcmp(p1, p2) == 0)
                {
                        return strlen(p1);      //如果匹配上，就返回
                }

                flag1 ++;
        }

        return 0;
}

void get_1_next(char *p, int plength)            //p为所求的字符串，plength为所求字符串的长度
{
        int i;
        for(i = 0; i < plength; i++)//不同的长度情况下，或者说next下标从0~len-1的情况
        {
                flag = 1;
                next[i] = get_2_next(p, i, flag);//因为根据定义，前缀和后缀不能到尾和首，所以flag
        }
}
https://blog.csdn.net/msdnwolaile/article/details/51287911
嗯嗯，对，这是我初步的想法，这样求得，但是，但是，但是，翻了翻资料，感觉在时间复杂度和空间复杂度方面太low了，别人的时间空间都是极少的，一定有优化的办法的，一定有
在求后续的next串的时候，完全没有必要去从最大的前缀去求，可以借用之前求到的next

如：串s  =  "ababc"          求next[4]

        由于我们已经知道了，next[3]    =   2,("aba" != "bab" , "ab" == "ab")，所以，我们非常的没有必要去做求

       （“abab”是不是等于“babc”）等等这些判断，因为从之前的next[1] = 0（可以知道“a”不等于“b”，也就是s[1]和s[0]直接的比较），

        所以当前我们要处理的就是：

        1，当前的字符（s[4]  = 'c'）是不是等于next[3]也就是（s[2]）,即就是判断s[2]是不是等于s[4]，如果相等：next[4]  =  next[3] + 1

        2，如果不相等的话，那么我们需要比较的就是s[4]是不是和s[next[next[3]]],由于next[3] = 2,那就是next[2],

              next[2]等于1，那么就是s[4]和s[1]进行比较，判断是否相等，如果相等next[4] = next[2] + 1并且退出;

        3，如果不想等的话，那么需要继续执行类似于我们上面的步骤，当带比较的字符为0的时候，那么就退出

　　

注意next的对称性
#include <stdio.h>
#include <string.h>

int next[30] = {0};

void get_1_next(char *p, int plength)            //p为所求的字符串，plength为所求字符串的长度
{
        int i, j,a;
        next[0] = 0; //没有前缀，也没有后缀
        for(i = 1; i < plength; i++)
        {
                j = i;
                while(1)
                {
                        if(p[next[j - 1]] == p[i])
                        {
                                next[i] = next[j - 1] + 1;
                                break;
                        }
                        else if(next[j - 1] == 0)
                        {
                                next[i] = 0;
                                break;
                        }
                        else
                        {
                                a = next[j - 1];   //这两行是为了说明 j = j- 1;（便于循环）
                                j = a + 1;
                        }
                }
        }
}

int main()
{
        int i;
        char p[30];
        int plength;

        scanf("%s", p);
        plength = strlen(p);
        get_1_next(p, plength); 

        for(i = 0; i < plength; i++)
        {
                printf("%c:%d\n", p[i], next[i]);
        }
        printf("\n");
}

　　

　　

　　

#include<string.h>
void makeNext(const char P[],int next[])
{//找到P数组的部分匹配表。
    int q,k;
    int m = strlen(P);//字符串长度
    next[0] = 0;//第一个元素，固定不变为0
    k = 0;
    for (q = 2; q <= m; ++q)//k从左往右0开始，同时它的移动表示成功匹配上的长度     q是确定长度，从1开始最大到m-1，匹配时，从右往左
    {
        while(k > 0 && P[q-1] != P[k])//当存在公共子串，或者说是部分匹配值时，
            k = next[k-1];//不匹配时，最原始的做法就是，k又从0开始，q确定还是q不变从右往左，求解出next[q]   注意next的对称性
//此处，子串不从0开始，而是从next[k-1]继续与q进行匹配，依次递推，压缩空间去搜索。

// 充分利用子串前缀和后缀的对称性，加快搜索速度
        if (P[q-1] == P[k])//当匹配上时，则k移动一步
        {
            k++;//匹配上的长度
        }
        next[q-1] = k;//记录部分匹配值
    }
}

int kmp(const char T[],const char P[],int next[])
{
    int n,m;
    int i,q;
    n = strlen(T);
    m = strlen(P);
    makeNext(P,next);
    for (i = 0,q = 0; i < n; ++i)//长串q移动一位
    {
        while(q > 0 && P[q] != T[i])//长串q位置不动
            q = next[q-1];//当不等时，匹配子串P从next[q-1]开始匹配  i不变
        if (P[q] == T[i])//当相等时，子串移动一位
        {
            q++;
        }
        if (q == m)//标识已经匹配到子串最后一个子串
        {//返回长串中的子串起始位置， i-m+1
            printf("Pattern occurs with shift:%d\n",(i-m+1));
        }
    }
}

int main()
{
    int i;
    int next[20]={0};
    char T[] = "ababxbababcadfdsss";
    char P[] = "abcdabd";
    printf("%s\n",T);
    printf("%s\n",P );
    // makeNext(P,next);
    kmp(T,P,next);
    for (i = 0; i < strlen(P); ++i)
    {
        printf("%d ",next[i]);
    }
    printf("\n");

    return 0;