Eigen解线性方程组

一. 矩阵分解：

矩阵分解 (decomposition, factorization)是将矩阵拆解为数个矩阵的乘积，可分为三角分解、满秩分解、QR分解、Jordan分解和SVD（奇异值）分解等，常见的有三种：1)三角分解法 (Triangular Factorization)，2)QR 分解法 (QR Factorization)，3)奇异值分解法 (Singular Value Decompostion)。

1. LU三角分解：
   
   三角分解法是将原正方 (square) 矩阵分解成一个上三角形矩阵　或是排列(permuted) 的上三角形矩阵和一个 下三角形矩阵，这样的分解法又称为LU分解法。它的用途主要在简化一个大矩阵的行列式值的计算过程，求 反矩阵，和求解联立方程组。不过要注意这种分解法所得到的上下三角形矩阵并非唯一，还可找到数个不同 的一对上下三角形矩阵，此两三角形矩阵相乘也会得到原矩阵。
   
   MATLAB以lu函数来执行lu分解法， 其语法为[L,U]=lu(A)。
2. QR分解：
   
   QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵,所以称为QR分解法,与此正规正交矩阵的通用符号Q有关。
   
   MATLAB以qr函数来执行QR分解法， 其语法为[Q,R]=qr(A)。
   
   3. 奇异值分解：
   
   奇异值分解 (singular value decomposition,SVD) 是另一种正交矩阵分解法；SVD是最可靠的分解法，但是它比QR 分解法要花上近十倍的计算时间。[U,S,V]=svd(A)，其中U和V分别代表两个正交矩阵，而S代表一对角矩阵。 和QR分解法相同， 原矩阵A不必为正方矩阵。使用SVD分解法的用途是解最小平方误差法和数据压缩。
   
   MATLAB以svd函数来执行svd分解法， 其语法为[S,V,D]=svd(A)。
3. LLT分解：
   
   A=LL^T
   
   Cholesky 分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零，故分解的下三角的对角元也是大于零的（LU三角分解法的变形）。
   
   5. LDLT分解法：
   
   若A为一对称矩阵且其任意一k阶主子阵均不为零，则A有如下惟一的分解形式：
   
   A=LDL^T
   
   其中L为一下三角形单位矩阵（即主对角线元素皆为1），D为一对角矩阵（只在主对角线上有元素，其余皆为零），L^T为L的转置矩阵。
   
   LDLT分解法实际上是Cholesky分解法的改进，因为Cholesky分解法虽然不需要选主元，但其运算过程中涉及到开方问题，而LDLT分解法则避免了这一问题，可用于求解线性方程组。
   
   二. 代码使用：

<span style="font-size:18px;">
#include <iostream>
#include <Eigen/Dense>
 using namespace std;
using namespace Eigen;
int main()
{
//线性方程求解 Ax =B;
 	Matrix4d A;
 	A << 2,-1,-1,1,        		 1,1,-2,1,        		 4,-6,2,-2,        		 3,6,-9,7;
Vector4d B(2,4,4,9);
	Vector4d x = A.colPivHouseholderQr().solve(B);
	Vector4d x2 = A.llt().solve(B);
	Vector4d x3 = A.ldlt().solve(B);
   	std::cout << "The solution is:\n" << x <<"\n\n"<<x2<<"\n\n"<<x3 <<std::endl;
}
</span>

注意：

我用上面代码计算出来，只有A.colPivHouseholderQr().sole(B)，算出来的是正常。其他都是错误，我就先使用这个公式运算吧，等我忙完这一阵子，在来研究一下。

运行结果：

colPivHouseholderQr:
0
-1
-4
-3
llt:
-289.143
448.714
29.9082
3.97959
ldlt:
1.52903
0.1758
-0.340206
0.0423223

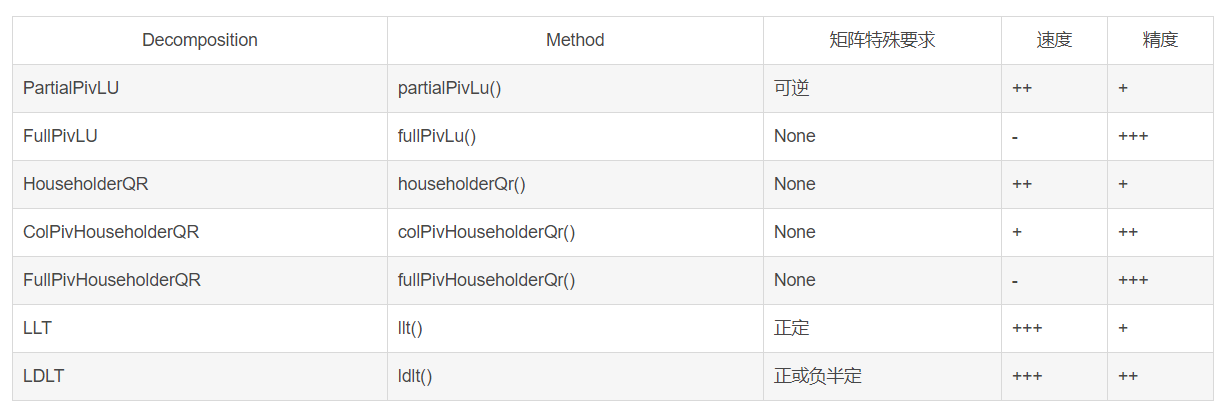
除了colPivHouseholderQr、LLT、LDLT，还有以下的函数可以求解线性方程组，请注意精度和速度：解小矩阵（4*4）基本没有速度差别

// Solve Ax = b. Result stored in x. Matlab: x = A \ b.
x = A.ldlt().solve(b));  // A sym. p.s.d.    #include <Eigen/Cholesky>
x = A.llt().solve(b));  // A sym. p.d.      #include <Eigen/Cholesky>
x = A.lu().solve(b));  // Stable and fast. #include <Eigen/LU>
x = A.qr().solve(b));  // No pivoting.     #include <Eigen/QR>
x = A.svd().solve(b));  // Stable, slowest. #include <Eigen/SVD>
// .ldlt() -> .matrixL() and .matrixD()
// .llt()  -> .matrixL()
// .lu()   -> .matrixL() and .matrixU()
// .qr()   -> .matrixQ() and .matrixR()
// .svd()  -> .matrixU(), .singularValues(), and .matrixV()

本文转自 ChenYuanshen 的CSDN 博客 ：https://blog.csdn.net/u013354805/article/details/48250547?utm_source=copy