kmp算法理解与记录

字符串匹配的暴力解法

给定字符串s和p，寻找字符串p在字符串s中出现的位置，暴力解法如下所示：

• 如果当前字符匹配成功，++i;++j,继续匹配下一字符。
• 如果s[i]与s[j]匹配失败，令i-=(j-1),j=0,即i转到上次首次匹配开头字符的下一位置，j从头开始。

int brute_match(string s, string p) {
  int slen = s.size();
  int plen = p.size();
  int i = 0, j = 0;
  while (i < slen and j < plen) {
    if (s[i] == p[j]) {
      ++i;
      ++j;
    } else {
      i -= (j - 1);
      j = 0;
    }
  }
  if (j == plen)
    return i - j;
  return -1;
}

如果有一种算法能够不让i回退，只需要移动j，那么我们的算法将会大为简化。

kmp算法

在kmp算法中，引入了next数组，表示当前字符之前的子字符串中具有多大长度的相同的前缀后缀，请注意，next字符串的内容是和需要匹配的字符串p相关的。

在brute-force算法的基础上改进的kmp算法如下所示：

int kmp_match(string s, string p,const vector<int> &next) {
  int slen = s.size();
  int plen = p.size();
  int i = 0, j = 0;
  while (i < slen and j < plen) {
    if (j == -1 or s[i] == p[j]) {
      ++i;
      ++j;
    } else {
      j = next[j];
    }
  }
  if (j == plen)
    return i - j;
  return -1;
}

next数组的求法

首先，我们思考一下如何计算给定字符串的最长相同前缀和后缀的长度。

1. 设最长相同前缀后缀为str
2. 设数组len中每一个位置和字符串s一对应，表示字符串截止到当前位置最长相同前缀后缀的长度。
3. k表示当前位置及之前的字符串的最长相同前缀后缀的长度。s[k]表示原字符串s在最长前缀后缀str之后紧跟的那个字符。
4. 我们从第2个字符开始寻找最长前缀后缀，如果s[i]!=s[k],代表字符i无法进一步与字符j匹配，最长相同前缀后缀不可能在上一次匹配的基础之上进一步增长。如果之前能够匹配的最长相同前缀后缀长度大于0，我们不断尝试在上一次的基础之上降低标准，匹配更小长度的最长前缀后缀。
5. 关键点在于，如何选择降低标准后的需要匹配的相同前缀后缀？这里我们将k调整为k=len[k-1],原因稍后详述。
6. 若最终经过调整之后，s[i]=s[j],这表示最长相同前缀与后缀能够在长度为k的最长相同前缀后缀的基础之上，再增长一个字符,即len[i]=++k。否则说明当前位置没有相同前缀后缀，记len[i]=0。

只有长度大于1的字符串才有最长前缀与后缀,最长前缀不包括最后一个字符，最长后缀不包括第一个字符。

k=len[k-1]原因讲解

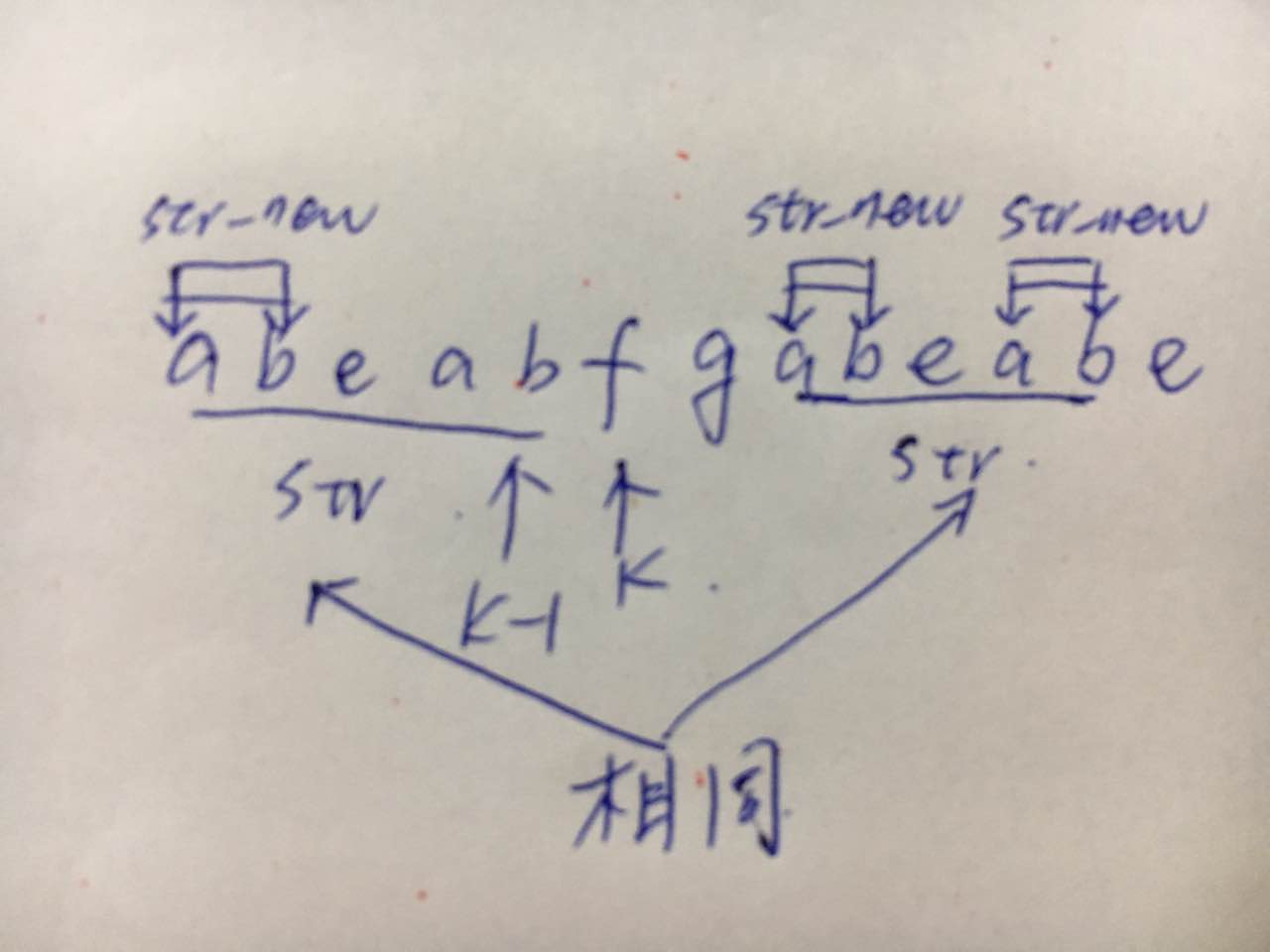
假设当前k指向字符串中f对应的位置，在e之前我们匹配到的最长相同前缀后缀为abeab,我们发现e与f不能匹配，我们需要降低标准，尝试匹配更短长度的最长前缀后缀，应该匹配多长的呢？

我们发现图中下划线部分的字符串str完全相同，我们要找的长度缩减的最长相同前缀后缀长度不能超过str的长度，而且要保证这一字符串(设为str_new)满足条件：是相同的前缀后缀。即图中最前面和最后面标记的字符串str_new必须完全一样。根据对称性，这等价于在靠后的str中寻找最长前缀后缀。而且因为k比较的时候，k实际指向前面str的末尾下一位置，所以我们有：k=len[k-1]。

void calculate_length(string s, vector<int> &len) {
  len.resize(s.length());
  len[0] = 0;
  int k = 0;
  for (int i = 1; i < s.length(); ++i) {
    while (s[i] != s[k] and k > 0) {
      k = len[k - 1];
    }
    if (s[i] == s[k]) {
      len[i] = ++k;
    } else {
      len[i] = 0;
    }
  }
}

next数组与最长前缀后缀

next数组，表示当前字符之前的子字符串中具有多大长度的相同的前缀后缀，也就是说next 数组相当于“最大长度值” 整体向右移动一位，然后初始值赋为-1。

其示例代码如下所示，因为和求最长前缀后缀的代码类似，故不再追究。

void calculate_next(string s,vector<int>&next){
  next.resize(s.length());
  int len = s.length();
  next[0] = -1;
  int k = -1;
  int j = 0;
  while(j<len-1){
    if(k == -1 or s[j] ==s[k]){
      ++k;
      ++j;
      next[j] = k;
    }
    else{
      k = next[k];
    }
  }
}