软间隔分类——SVM

引入：
1、 数据线性不可分；
2、 映射到高维依然不是线性可分
3、 出现噪声。
如图：

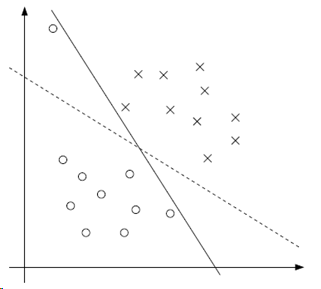
对原始问题变形得到#2：

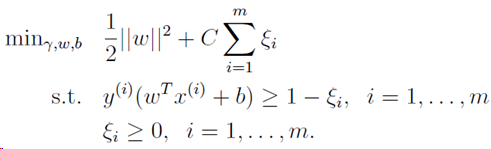
进行拉格朗日转换：

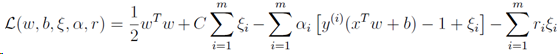
其中α和r是拉格朗日因子，均有不小于0的约束。
按照之前的对偶问题的推导方式，先针对w，b最小化，然后再针对α最大化，得到新的对偶问题：

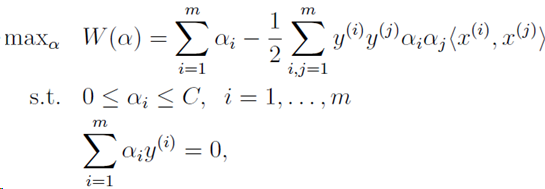
求解得到α之后，w仍然按公式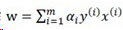给出，但是截距b的计算方式要改变。

KKT中的互补条件也变为了：【有待深入理解其含义】

---

---

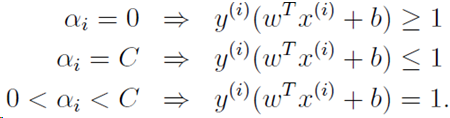
KKT的理解：【首先得注意：（1）α_i与样本(x⁽ⁱ⁾,y⁽ⁱ⁾)是一一对应的；（2）α_i>=0】

由对w的偏导得到：

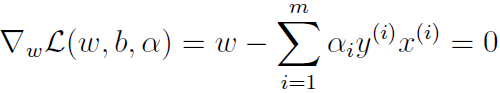（a）

这个约束可以用来在得到α之后求w

而对b的偏导得到：

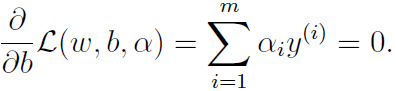
这个已经进入优化的约束条件。

而根据w的计算公式(a)可以得知，w的计算其实只依赖α_i>0大于0的样本，这些样本就称为支持向量（对于软件隔分类也是一样）。

对于线性可分支持向量机，KKT的另外三个约束条件为：

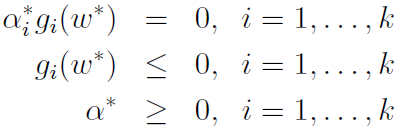
其中：

　　

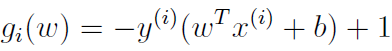
最优解满足：函数距离大于1的大多数样本(g_i(w)>0)，其对应的α_i=0，函数距离等于的1的样本(g_i(w)=0，支持向量)，其对应的α_i>0

对于软间隔分类，KKT的另外三个约束条件为：

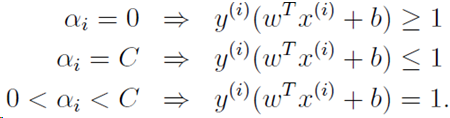
最优解满足：函数距离大于1的大多数样本(g_i(w)>0)，其对应的α_i=0，函数距离等于的1的样本(g_i(w)=0，支持向量)，其对应的0<α_i<C

　　　　　　函数距离小于的1的样本(g_i(w)=0，支持向量)，其对应的α_i=C

这些条件用于判断SMO算法是否收敛。

第一个式子表明在两条间隔线外的样本点前面的系数为0，离群样本点前面的系数为C，

而在超平面两边的最大间隔线上的样本点前面系数在(0,C)上。

支持向量包括α_i=C的点吗？我觉得包括，毕竟它影响到了w的计算