二维凸包 Graham扫描算法

题目链接：

http://poj.org/problem?id=1113

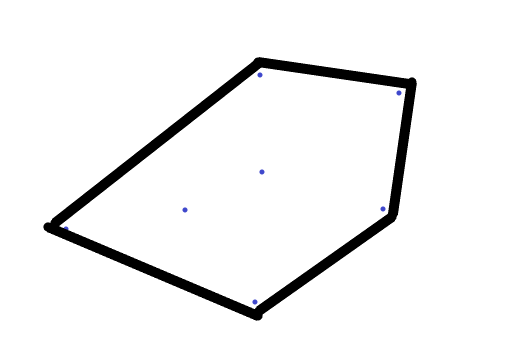
求下列点的凸包

求得凸包如下：

Graham扫描算法：

找出最左下的点，设为一号点，将其它点对一号点连线，按照与x轴的夹角大小排序：

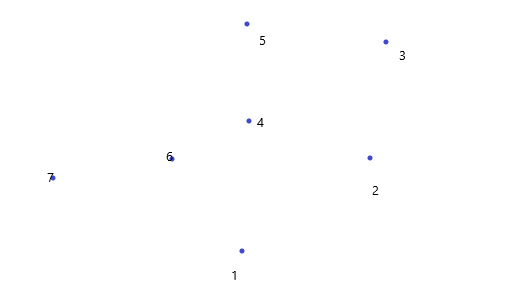
让点1,2入栈，从第三个点开始循环

步骤1：判断该点是否在栈顶第二个点和栈顶的点的连线的左边，

2.如果在左边，将该点入栈，继续循环，

3.如果不在，弹出栈顶点，重复步骤1，

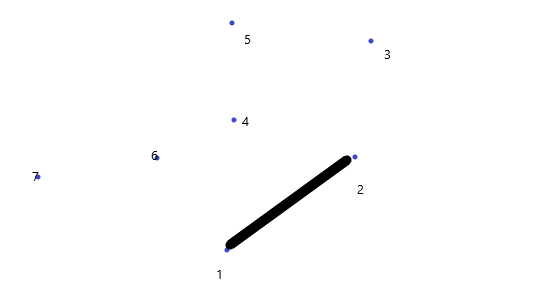
3在1，2连线左边，3入栈

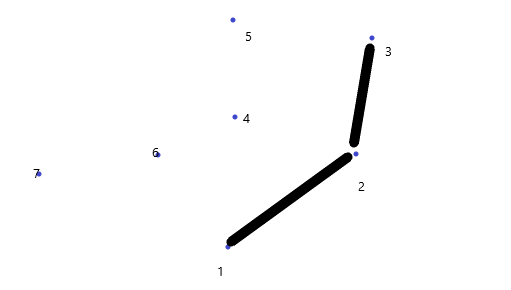
4在2,3连线左边，4入栈

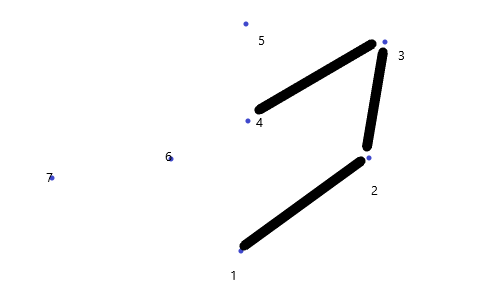
5不在3,4连线左边，4出栈，5在2,3连线左边，5入栈

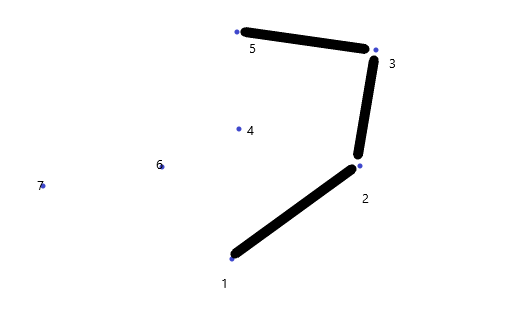
6在3,5连线左边，6入栈

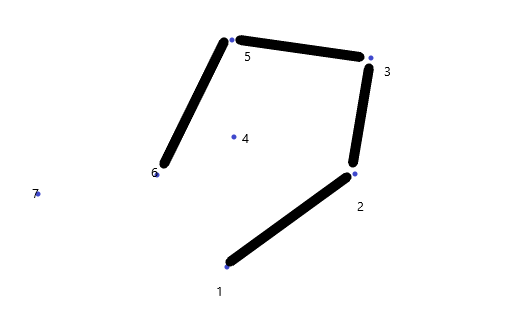
7不在5,6连线左边，6出栈，7在3,5连线左边，7入栈

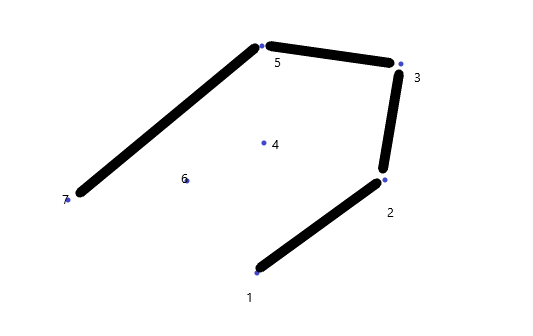
遍历完成后，将栈顶与1连起来就完成了

代码

//#include<bits/stdc++.h>
#include<iostream>
#include<cmath>
#include<algorithm>
#define fi first
#define se second
#define INF 0x3f3f3f3f
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define pqueue priority_queue
#define NEW(a,b) memset(a,b,sizeof(a))
#define lowbit(x) ((x)&(-x))
using namespace std;
const double pi=4.0*atan(1.0);
const double e=exp(1.0);
const int maxn=4e4+;
typedef long long LL;
typedef unsigned long long ULL;
const LL mod=1e9+;
const ULL base=1e7+;
struct Point{
    int x,y;
    bool operator<(Point &u){//坐标排序
        if(x!=u.x) return x<u.x;
        return y<u.y;
    }
};
Point vex[maxn],Stack[maxn],Basis;
short checkL(Point p,Point q,Point s){//判断点s是否在直线pq的左侧
    int area2=p.x*q.y-p.y*q.x+q.x*s.y-q.y*s.x+s.x*p.y-s.y*p.x;
    if(area2>) return ;//表示在左侧
    if(area2==) return ;//表示在同一条线上；
    return -;//表示在右侧
}
double dis(Point u,Point v){//计算uv的距离
    return sqrt((u.x-v.x)*(u.x-v.x)*1.0+(u.y-v.y)*(u.y-v.y));
}
bool cmp(Point a,Point b){//极角排序
    short m=checkL(Basis,a,b);
    if(m==) return ;//b在基点与a的连线的左侧，说明b的极角大于a
    if(m==&&dis(Basis,a)<=dis(Basis,b))//极角相同时，靠近基点的排在前
        return ;
    return ;
}
int main(){
    cin.tie();
    cout.tie();
    int n,l;
    cin>>n>>l;
    for(int i=;i<n;i++){
        cin>>vex[i].x>>vex[i].y;
    }
    sort(vex,vex+n);
    Basis=vex[];//选第一个点为基点
    sort(vex+,vex+n,cmp);
    int top=;
    Stack[top]=vex[];
    Stack[++top]=vex[];
    for(int i=;i<n;i++){
        while(top>=&&checkL(Stack[top-],Stack[top],vex[i])<){
            top--;
        }
        Stack[++top]=vex[i];
    }
    double sum=0.0;
    for(int i=;i<top;i++){
        sum+=dis(Stack[i],Stack[i+]);
    }
    sum+=dis(Stack[top],Stack[]);
    sum+=2.0*pi*l;
    LL ans=(LL)sum;
    if(sum-(double)ans>=0.5){
        ans++;
    }
    cout<<ans<<endl;
    system("pause");
    return ;
}