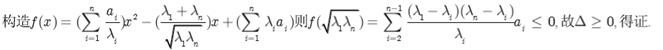MT【39】构造二次函数证明
这种构造二次函数的方法最早接触的应该是在证明柯西不等式时:


再举一例:


最后再举个反向不等式的例子:
评:此类题目的证明是如何想到的呢?他们都有一个明显的特征$AB\ge(\le)C^2$,此时构造二次函数利用$\Delta$证明,效果非常理想.
MT【39】构造二次函数证明的更多相关文章
- MT【219】构造二次函数
(2012北大保送)已知$f(x)$是二次函数,且$a,f(a),f(f(a)),f(f(f(a)))$是正项等比数列;求证:$f(a)=a$ 构造二次函数$f(x)=qx$,则$a,f(a),f(f ...
- MT【114】构造二次函数
评:b+c,bc好比向量里的一组基底,可以将关于b,c的对称式表示出来.
- MT【206】证明整数数列
已知方程$x^3-x^2-x+1=0$,的三根根为$a,b,c$,若$k_n=\dfrac{a^n-b^n}{a-b}+\dfrac{b^n-c^n}{b-c}+\dfrac{c^n-a^n}{c-a ...
- MT【63】证明不是周期函数
证明$f(x)=sinx^2$不是周期函数. 反证:假设是周期函数,周期为$T,T>0$. $$f(0)=f(T)\Rightarrow sinT^2=0\Rightarrow T^2=k_1\ ...
- MT【33】证明琴生不等式
解答:这里数学归纳法证明时指出关键的变形. 评:撇开琴生不等式自身的应用和意义外,单单就这个证明也是一道非常不错的练习数学归纳法的经典题目.
- MT【16】证明无理数(2)
证明:$sin10^0$为无理数. 分析:此处用$sin$的三倍角公式,结合多项式有有理根必须满足的系数之间的关系可以证明. 评:证明$sin9^0$为无理数就不那么简单.思路:先利用$sin54^0 ...
- MT【15】证明无理数(1)
证明:$tan3^0$是无理数. 分析:证明无理数的题目一般用反证法,最经典的就是$\sqrt{2}$是无理数的证明. 这里假设$tan3^0$是有理数,利用二倍角公式容易得到$tan6^0,tan1 ...
- E - Rebuild UVALive - 7187 (二次函数极值问题)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5531 Problem Description Archaeologists find ruins of ...
- Line Search and Quasi-Newton Methods 线性搜索与拟牛顿法
Gradient Descent 机器学习中很多模型的参数估计都要用到优化算法,梯度下降是其中最简单也用得最多的优化算法之一.梯度下降(Gradient Descent)[3]也被称之为最快梯度(St ...
随机推荐
- width,height为多少px时,A4纸打印时刚好一页?
计算方式一般的分辨率为XX像素/英寸,其中一英寸为25.4毫米.所以一毫米的像素数就为XX/25.4.现在的工作就是求XX的值了,把XX的值求出来以后,直接用XX/25.4 * 210就得到A4纸的像 ...
- 从源码的角度看 React JS 中批量更新 State 的策略(上)
在之前的文章「深入理解 React JS 中的 setState」与 「从源码的角度再看 React JS 中的 setState」 中,我们分别看到了 React JS 中 setState 的异步 ...
- 原创超清的 Webpack2 视频教程
原文发表于我的技术博客 这是我免费发布的高质量超清「Webpack 2 视频教程」. Webpack 作为目前前端开发必备的框架,Webpack 发布了 2.0 版本,此视频就是基于 2.0 的版本讲 ...
- Oracle数据库设置为归档模式的操作方法
Oracle归档模式非常非常重要!对于有些数据库刚装好后可能是非归档模式,这是很危险的!为了安全起见,一定要谨记:对于Oracle数据库,一定要设置为归档模式,尤其是生产库,只有这样才能实现数据库的有 ...
- HTTP协议基础与web服务的重定向,跳转以及请求转发
JavaWeb中,HttpServletRequest与HttpServletResponse几乎是处理各种请求与操作必备的参数,与原始的ServletRequest/ServletResponse相 ...
- B. Interesting drink
链接 [http://codeforces.com/group/1EzrFFyOc0/contest/706/problem/B] 题意 给你n个数,q次查询,每次输入一个m,问n个数中有多少个数小于 ...
- 【2016.3.19】作业 分析一个很有(wu)趣(liao)的小程序
问题1:这个程序要找的是符合什么条件的数? 能够整除2-32中所有数仅除了在此之中的两个相邻的数,比如能整除2-29,且不能整除30,31.当然,这只是举个例子. 问题2:这样的数存在么?符合这一条件 ...
- 我的github地址
链接:https://github.com/long0123/test.git 推送项目的github的大致步骤如下: 1.在本地创建一个项目仓库,可以放些基本的项目文件 2.cd至该目录下 3. ...
- throws和throw抛出异常的使用规则
一直对java中的throws和throw不太理解.最近一直在查这两个方面的资料,算是能明白一点吧.如果我下面的观点哪有不对,希望指出来,我加以改进. throw:(针对对象的做法) ...
- vue 单文件 样式写了scoped 不能覆盖框架原有样式的解决办法
vue 单文件 样式写了scoped 不能覆盖框架原有样式的解决办法 在vue 里面<style scoped></style> 是为了让样式只影响本身自己组件的样式,不改变全 ...