【3.0 递归 Recursion 02】

【递归：阶乘】

1.寻找基本情况

对于阶乘而言，最基本的情况就是0！和1！，二者的结果都是1

我们不妨现在方法中写下这个情况，帮助我们跳出递归

if(i<=1){
return 1 ;
}

接下来，如果不是1或0，则进行阶乘运算

public static int Factorial (int i){
    if(i<=1){
    return 1 ;
    }else {
     return (i*Factorial(i - 1)) ;
  }
}

思路很简单，我们从n开始放入，计算n！就需要（n-1）!，计算(n-1)!需要(n-2)!，以此递推到1！

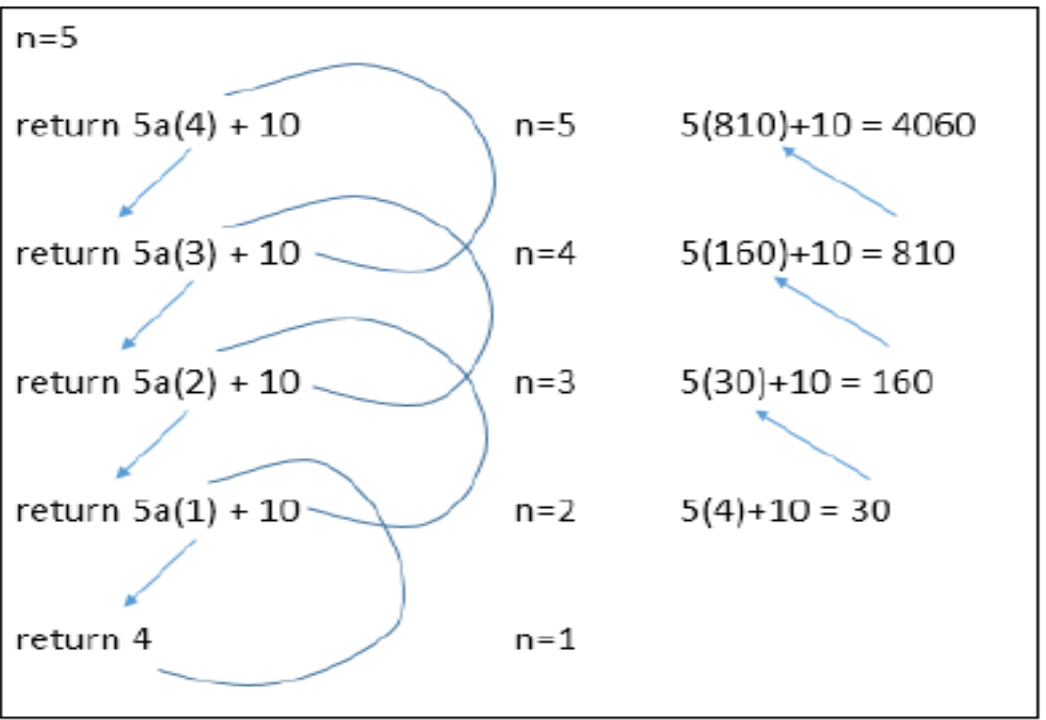
下面是对于这次操作的栈的示意图（以5为例）

建立堆栈（递归的过程）

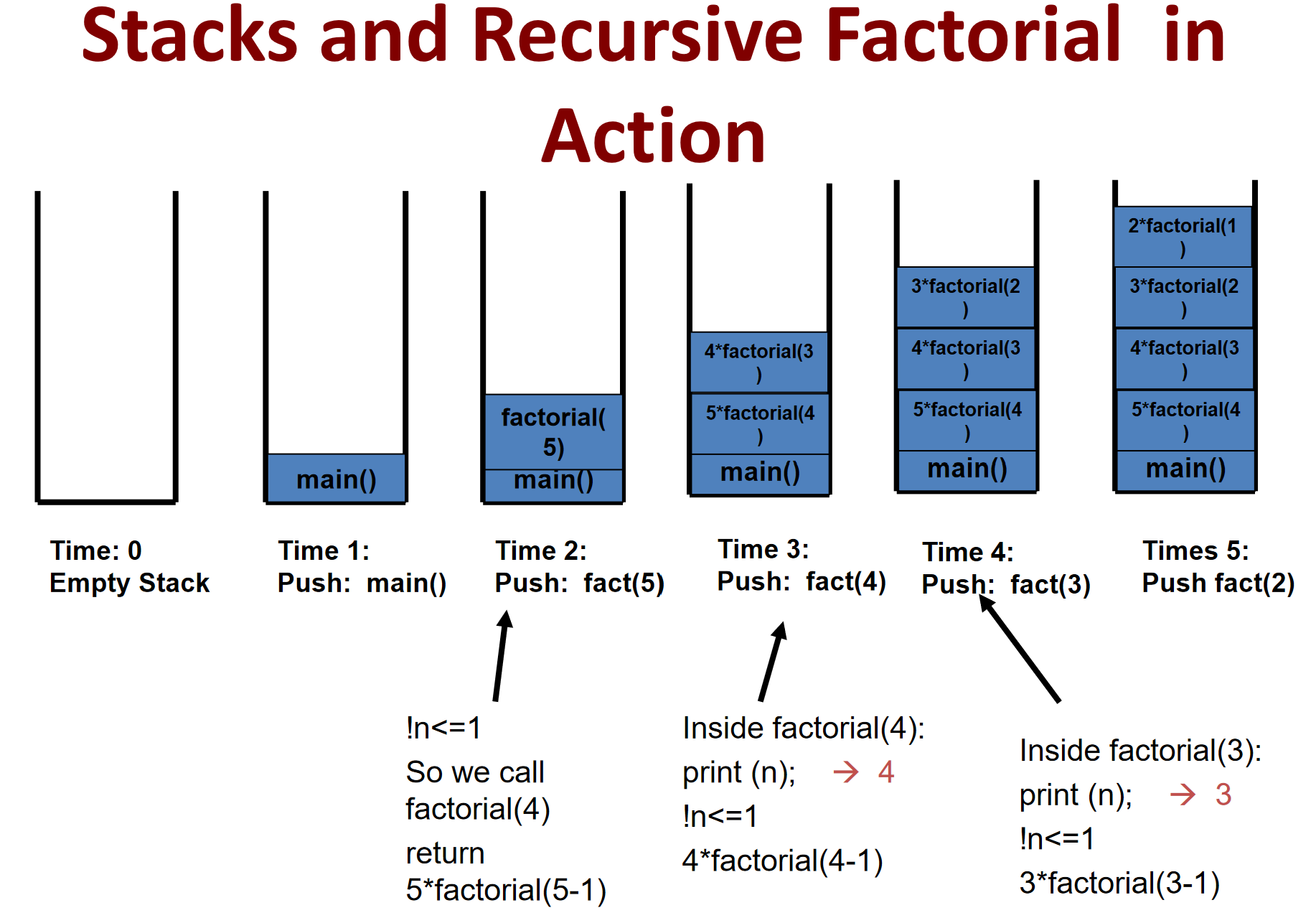
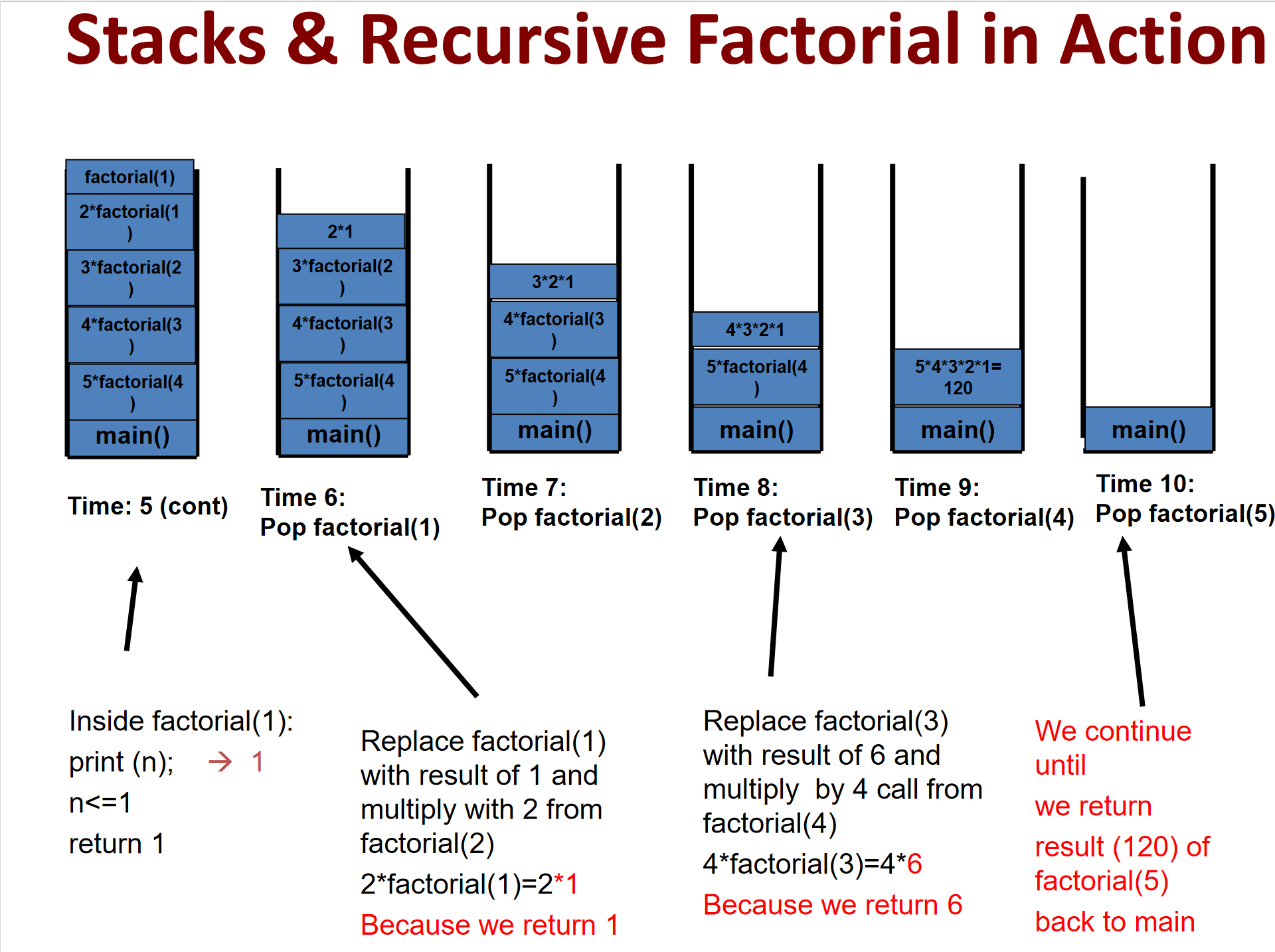
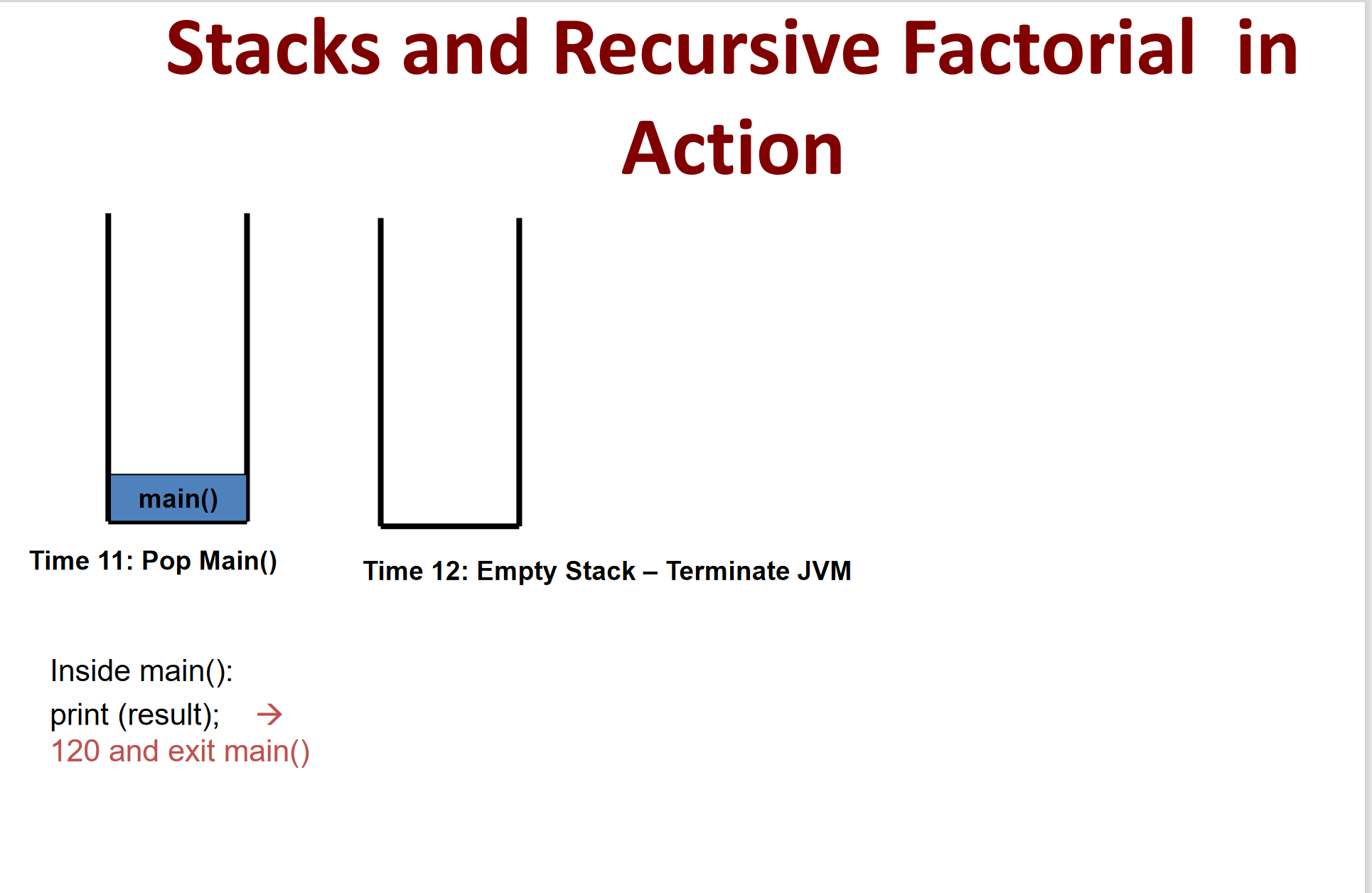
开始执行的时候，是从Factoria(1)逐级返回，最终得到5*4!即返回的过程

【递归：三角数】

三角数就像是加法的“阶乘”,必然1+2+3+4...

首先还是先寻找最初始的情况，显然那就是1了

和阶乘一样，我们也利用“堆栈——返回”的操作来进行三角数的计算

我们观察发现：出现一个模式即 T（n）= T（n –1）+ n 这种模式将有助于对三角数程序的递归进行程序编写。

public static int TrianNum(int i){
    if(i<=1){
    return 1 ;
    }else {
     return (i+TrianNum(i - 1)) ;
  }
}

【斐波纳契数列 Fibonacci Numbers】

斐波那契数列：前两个数之后的每一个数都是前两个数的和

我们可以通过下面这个方程来描述斐波纳契数列

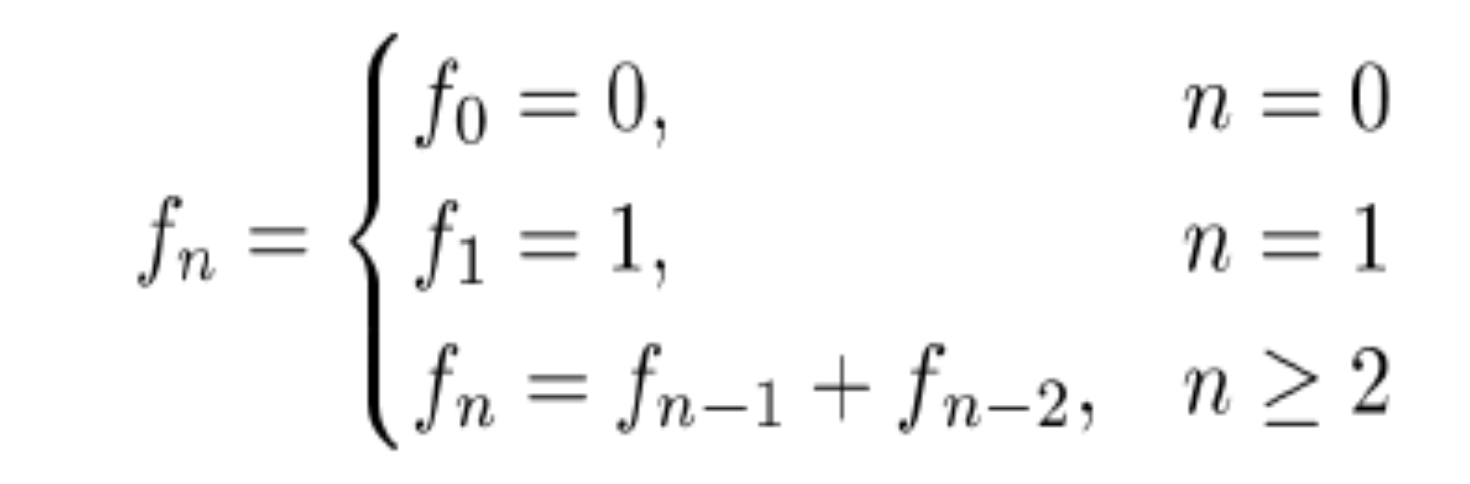
从迭代的角度来看斐波那契数列：

为了计算任何斐波那契数“n”，我们需要知道斐波那契数“n -1”和“n -2”，对于迭代版本，我们从第一个数字（n = 0）开始

随后我们计算1，2两个数字，之后是2,3，然后是3,4...以此不断推进，那么可以按照这个思想得到下面这个算法

public static int FibIter(int n){
  int prevl =0 , prev2 = 1 ;
  int savePrev1 = 0 ;
  for(int i = 0 ; i <n ; i ++){
    savePrev1 = prev1 ;
    prev1 = prev2 ;
    prev2 = savePrev1 + prev2 ;
  }
    return prev1 ;
}

从递归的角度来看斐波那契数列：

在之前的方程中，实质上已经包含的基本情况和递归步骤

我们可以得到在递归角度的如下代码：

public static int Fib(int n){
  if(n == 0 ) {
     return 0 ;
  }
  else if(n == 1 ) {
     return 1 ;
      //注意，这里是else if ，当第一个基本情况不满足时，才去判定第二个。当二者都不符合，再进入递归步骤
  }else{
    return Fib(n-1) + Fib(n-2) ;   //就是这一步，实质上实现了F(n) = F(n-1) + F(n-2) 的操作
}

迭代和递归两种方法得到的答案是一样的，但是运行的过程和核心是非常不同的

采用递归的思想进行计算时，先不断堆栈达到基本情况（0或1），然后再由基本情况向目标推进

【递归：函数功能定义 Functional Definitions】

我们经常会遇到用递归函数定义的问题——就像我们在斐波那契数列中看到的那样,问题的定义通常用数学的方法(方程)写成

就像这种形式的方程，我们便可以使用递归

在这种情况下，递归常常会比迭代更加直观

public static int FuncA(int n) {
    if(n == 1 ){
      return 4 ;
     }else{
      return (5* Func(n-1)+10);
      }
}

【递归与数组 Recursion with Arrays】

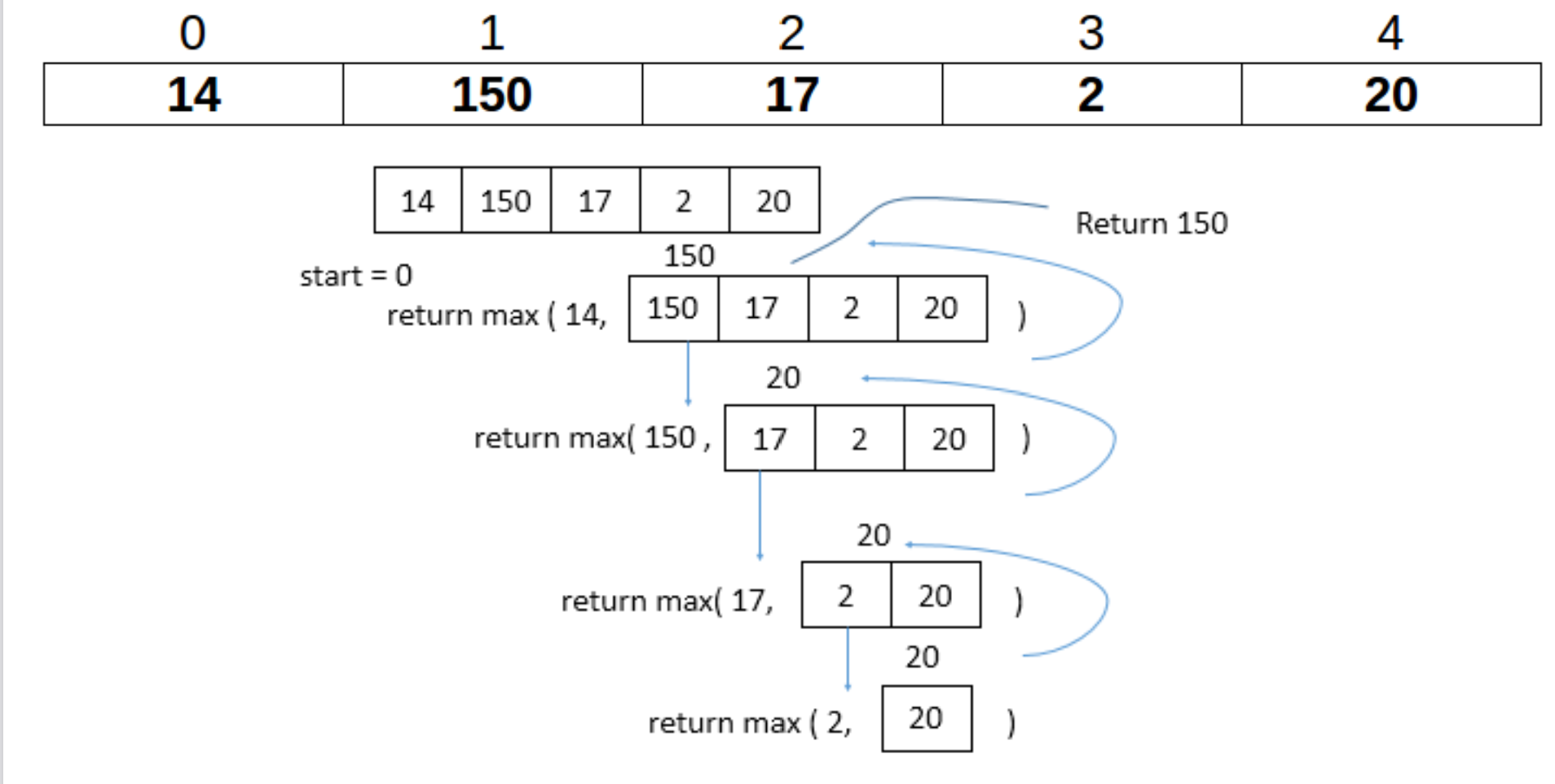
递归还可以用于查找存储在数组中的最大值和最小值，让我们尝试一个寻找数组最大值的例子：

首先是找到基本情况，我们将假定将从当前元素开始遍历整个数组。基本情况是，当我们查看数组中的最后一个元素的时候————这时候我们已经知道了我们遍历了数组中的所有元素，所以我们从此跳出递归

那么递归步骤呢，这个其实很简单：我们将每个元素与当前存储的最大元素进行比较，如果当前正在查看的元素大于当前最大存储元素，则将该值更新为新的最大值

附：Math.max ： Math.max(int a, int b)，会返回a、b中的较大者，需要import java.lang.* ; 后使用

public static int maxArray(int [] array , int start){
    if(start == array.lengrh - 1){
          return array[start] ;  //一个基本情况：仅有一个数字的数组，代表需要结束了
      }else{
          return (Math.max(array[start],maxArray(array,start + 1)));
        }
}

可能光看代码比较抽象，来看看这张示意图：

【小结：递归的优缺点】

缺点：

•递归反复调用该方法，该方法在内存和处理时间方面会产生成本

•每次递归调用都会创建该方法的另一个副本(及其所有变量)

•这种方法的复制会消耗大量的内存空间

优点：

•如果我们对原始问题做一些细微的改变，就会更容易找到递归的解决方案

•有时，递归解决方案的运行速度会比迭代解决方案慢，不过，在大多数情况下，它只是稍微慢一些

•在许多情况下，递归解决方案比迭代解决方案更容易理解和编写代码