神奇的魔方阵--(MagicSquare)(2)

在上一篇博客中,我们讨论了阶数为奇数,以及阶数为(4K)的魔方阵的排列规则,以及代码实现(详见:https://www.cnblogs.com/1651472192-wz/p/14640903.html);

本篇文章则对最后一种情况: 阶数n = 4K + 2 的魔方阵 排列规律 进行分析, 以及代码实现.让我们直接进入正题:

 1. 偶数阶魔方阵(n = 4*K + 2)

　　1.排列规律:(源自百度百科):

         1. 先将整个方阵划成田字型的四个2 k + 1阶的奇数阶小方阵

2. 右半两个小方阵中大于k+2的列；

3. 左半两个小方阵中( k + 1 , k + 1 )的格位；

4. 左半两个小方阵中除了( k+1 , 1 )是指第一列第k+1行的格位之外，小于k +1的列。

5. 以奇数阶魔方阵的方法连续填制法依左上、右下、右上、左下的顺序分别填制这四个小方阵。

         6. 将上半及下半方阵中有注记的数字对调，魔方阵完成。

 

　　2. 规律解读:

　　 我们可以将排列规律分成两个部分,

　　 1. 分块,并对所分的块儿 按照 左上、右下、右上、左下的顺序分别以奇数魔方阵的摆放规则进行摆放(注意 : 在填写时要接上上个魔方阵的最后一个数字开始填起),

　　 2. 对魔方阵的特殊位置进行标记 ,在最后对上下对称的标记的位置的数字进行对调.

 

　　3. 图示:(在这里以6阶魔方阵为例)

 　　1.分块:

　　

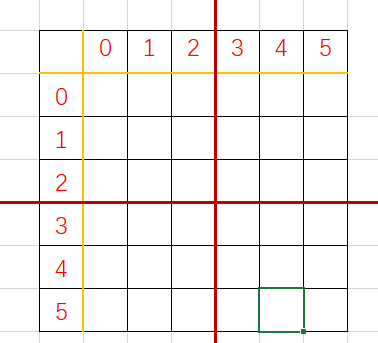
　　2. 按照 左上、右下、右上、左下的顺序分别以奇数魔方阵的摆放规则进行摆放 , 同时标记:

　　 

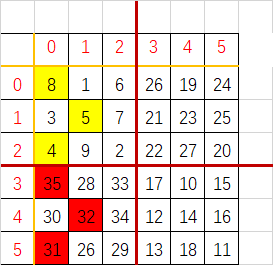
　　3.对标记的方块进行对调,魔方阵完成:

　　

　　4.代码实现:

　　根据上面的分析,代码主要分为两部分 1. 分块填数, 2. 交换

　　代码如下:(软件:VS2019)

#include<assert.h>
#include<stdio.h>

void Print(int(*ar)[6], int row, int col)//打印
{
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            printf("%3d", ar[i][j]);
        }
        printf("\n");
    }
}

//传入 奇数阶小魔方阵起始的行列信息,以及小魔方阵的大小,起始的数字
void Magic_Square_1(int (*ar)[6],int row, int col, int size, int num)
{
    assert(ar != nullptr && row >= 0 && col >= 0);
    ar[row][size / 2 + col] = num;//注意第一个数摆在魔方阵第row行中间的位置
                                  // 在这里不能取col/2,要取 size/2 + col;
    int preRow = row;//记录上一个数字的行对于[row][col] 的偏移量 信息
    int preCol = size / 2 + col;

    for (int i = num +1; i < num + size * size; i++)
    {
        //重点:
        //注意在这里行列下标都需要加上传入的row 和 col 即在这里的preRow 和 preCol 记录的是相对与
        //坐标[row][col]的偏移量.
        if (ar[row + (preRow - 1 + size) % size][col + (preCol + 1) % size] == 0)
        {
            ar[row + (preRow - 1 + size) % size][col + (preCol + 1) % size] = i ;
            preRow = (preRow - 1 + size) % size;
            preCol = (preCol + 1) % size;
        }
        else
        {
            ar[row + (preRow + 1) % size][col + preCol] = i;
            preRow = (preRow + 1) % size;
        }
    }
}

void Swap(int* pa, int* pb)
{
    int tmp = *pa;
    *pa = *pb;
    *pb = tmp;
}

void Magic_Square()
{
#define ROW 6
#define COL ROW
    int ar[ROW][COL] = {};
    Magic_Square_1(ar,   0,     0,    ROW / 2,              1);//左上
    Magic_Square_1(ar, ROW/2, COL/2,  ROW / 2,  1+(ROW*COL/4));//右下
    Magic_Square_1(ar,   0,   COL/2,  ROW / 2,  1+ (ROW * COL / 2));//右上
    Magic_Square_1(ar, ROW/2,    0,   ROW / 2,  1+ (ROW * COL / 4)*3);//左下

    //上下对调右半两个小方阵中大于k+2的列；
    for (int i = 0; i < ROW/2; i++)
    {
        for (int j = 0; j < COL; j++)
        {
            //上下对调右半两个小方阵中大于k+2的列；
            if (j > ((ROW - 2) / 4 + ROW/2 + 2)) // 此处 注意需要加上  ROW/2
            {
                Swap(&ar[i][j], &ar[i + ROW / 2][j]);
            }

            //左半两个小方阵中除了( k+1 , 1 )是指第一列第k+1行的格位之外，小于k +1的列。
            if(j < ((ROW - 2) / 4 ) ) //此处注意在程序中,下标是从零开始的,所以不需要加1 即:if(j < ((ROW - 2) / 4  + 1)) 这样是错误的
            {
                if (j != 1  &&  i != ((ROW - 2) / 4 ))//同上不需要加一
                {
                    Swap(&ar[i][j], &ar[i + ROW / 2][j]);
                }
            }
        }
    }

    //左半两个小方阵中( k + 1 , k + 1 )的格位；
    Swap(&ar[ROW / 4][COL / 4], &ar[ROW / 4 + ROW / 2][COL / 4]);
    Print(ar, ROW, COL);

#undef ROW
#undef COL

}

int main()
{
    Magic_Square();
    return 0;
}

运行结果:

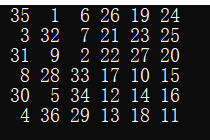
(若有大哥发现其中的不合适或者错误,请务必在评论中告知,小弟在这里祝大哥心情愉悦,生活快乐!)

本篇完.