【leetcode】85. Maximal Rectangle（单调栈）

Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

Example 1:

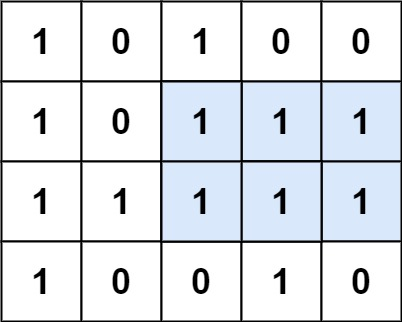
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 6
Explanation: The maximal rectangle is shown in the above picture.

Example 2:

Input: matrix = []
Output: 0

Example 3:

Input: matrix = [["0"]]
Output: 0

Example 4:

Input: matrix = [["1"]]
Output: 1

Example 5:

Input: matrix = [["0","0"]]
Output: 0

参考84题的单调栈解法

求最大矩形=》求解包含当前柱子的最大矩阵=》就两端第一个小于该柱子的索引位置=>利用单调递增栈 （两端初始化一个0）

单调递减栈可以用来求两端第一个大于该柱子的索引值 （两端初始化一个极大值） 便于后面弹栈

CPP 代码

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        // 利用单调栈进行求解
        if(matrix.size()==0) return 0;
        int m=matrix.size(),n=matrix[0].size();
        vector<int> dp(n,0);
        int res=0;
        for(int i=0;i<m;++i){
            dp.resize(matrix[i].size());
            for(int j=0;j<n;++j){
                if(matrix[i][j]=='0'){
                    dp[j]=0;
                }
                else{
                    dp[j]=dp[j]+1;
                }
            }
            int tmp=calrect(dp);
            res=max(res,tmp);
        }
        return res;

    }
    int calrect(vector<int> dp){
        dp.push_back(0);
        dp.insert(dp.begin(),0);
        stack<int>ss;
        int n=dp.size();
        int res=0;
        for(int i=0;i<n;++i){
            while(ss.size() && dp[ss.top()]>dp[i]){
            int tmp=ss.top();ss.pop();
            res=max(res,dp[tmp]*(i-ss.top()-1));
            }
            ss.push(i);
        }
        return res;
    }
};

Python 代码

class Solution(object):
    def maximalRectangle(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """
        #这题如何暴力法求解呢？
        #能不能换成柱子 好像不行哎
        #利用单调栈
        if not matrix:
            return 0
        m=len(matrix)
        n=len(matrix[0])
        stack=[0]*n
        res=0
        for i in range(m):
            for j in range(n):
                if matrix[i][j]=="0":
                    stack[j]=0
                else:
                    stack[j]+=1
            #启用单调栈来计算当前柱子的最大面积
            are=self.calrect(stack)
            res=max(are,res)

        return res

    def calrect(self,height): #单调栈求最大面积
        height=[0]+height+[0]
        stack=[]#维护一个单调递增栈 统计每个柱子两边第一个比他小的柱子
        n=len(height)
        res=0
        for i in range(n):
            while stack and height[stack[-1]]>height[i]:
                tmp=stack.pop()
                are=(i-stack[-1]-1)*height[tmp]
                res=max(res,are)
            stack.append(i)
        return res