KMP算法初探

[edit by xingoo]

kmp算法其实就是一种改进的字符串匹配算法。复杂度可以达到O(n+m)，n是参考字符串长度，m是匹配字符串长度。

传统的算法，就是匹配字符串与参考字符串挨个比较，如果相同就比较下一个，如果不相同，就返回上一次的结果，再重新比较。

如图1 如果失败则字符串会重新用S(参考字符串)的第二个，与T(匹配字符串)的第一个比较，知道全部符合查找，或找不到为止。

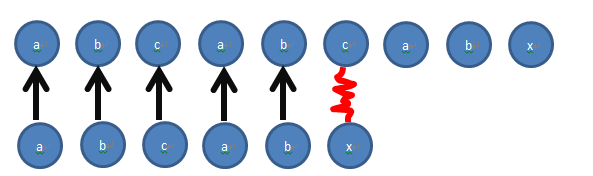
此时发现S[5] != T[5],因此用S[1]与T[0]进行比较。

此时发现S[1]!=T[0],因此用S[2]与T[0]比较。

此时，仍然不相等，继续后移。

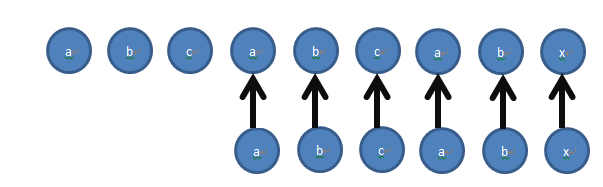
此时，S[3] == T[0],继续比较，发现所有T元素都在S中找到，满足查找，返回开始匹配的下标3.

传统代码

 int old_index(char * S,char * T){
     int i=;
     int j=;
     while(i<strlen(S) && j<strlen(T)){
         if( S[i] == T[j] ){
             ++i;
             ++j;
         }
         else{
             i = i-j+; //上一次的下一个
             j=;
         }
     }
     if(j == strlen(T))
         return i-strlen(T);
     else
         return -;
 }

这种比较忽略了一个问题，就是在T中，abcabx，第一个字符串因为不跟第二个，第三个一样，因此，在一开始的匹配中，可以直接跳过比较，直接从S的第三个元素开始比较。这里就涉及到一个概念：最短子串对称匹配。

首先，初始化，当j=0时，next(j)=-1;

当j=1时，字符串0到j-1,只有"a",因此 next(j) = 0；

当j=2时，字符串0到j-1，字符串为"ab"，因此next(j) = 0；

当j=3时，字符串0到j-1，字符串为"abc",因此next(j) = 0;

当j=4时，字符串0到j-1，字符串为"abca",此时，前缀a在末尾出现，因此next(j) = 1;

当j=5时，字符串0到j-1，字符串为"abcab"，此时，前缀ab在末尾出现，因此next(j) = 2;

最后得到next的数组为"-1 0 0 0 1 2"。

按照这个方法：

ababab的next数组为"-1 0 0 1 2 3 4"

这里面，当j=5时，字符串"ababa",前缀是"aba",后缀也是"aba"，因此next值为3.

计算next数组详细代码

void getNext(char * T,int *next){
    int i,j;
    i=;
    j=-;
    next[]=-;
    while(i<strlen(T)){
        if(j == - || T[i] == T[j]){
            ++i;
            ++j;
            next[i] = j;
        }
        else{
            j = next[j];
        }
    }
}

kmp匹配代码

int kmp(char* S,char * T){
    int i=;
    int j=;
    int next[MAX];
    getNext(T,next);
    while(i<strlen(S) && j<strlen(T)){
        printf("i %d-%c j %d-%c\n",i,S[i],j,T[j]);
        if(j== || S[i]==T[j]){
            ++i;
            ++j;
        }else{
            j = next[j];
            printf("j back to %d\n",j);
        }
    }
    if(j == strlen(T))
        return i-strlen(T);
    else
        return ;
}

全部代码

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>
 #define MAX 20

 void getNext(char * T,int *next);
 int kmp(char * S,char * T);
 int old_index(char * S,char * T);

 int main()
 {
     char * s = "acabbabababc";
     char * t = "ababab";

     //printf("the pos is:%d\n\n",old_index(s,t));
     //printf("the pos is:%d\n\n",old_index(m,t));
     //printf("the pos is:%d\n\n",old_index(n,t));
     printf("the pos is:%d\n",kmp(s,t));
     return ;
 }

 void getNext(char * T,int *next){
     int i,j;
     i=;
     j=-;
     next[]=-;
     while(i<strlen(T)){
         if(j == - || T[i] == T[j]){
             ++i;
             ++j;
             next[i] = j;
         }
         else{
             j = next[j];
         }
     }
 }

 int kmp(char* S,char * T){
     int i=;
     int j=;
     int next[MAX];
     getNext(T,next);
     while(i<strlen(S) && j<strlen(T)){
         printf("i %d-%c j %d-%c\n",i,S[i],j,T[j]);
         if(j== || S[i]==T[j]){
             ++i;
             ++j;
         }else{
             j = next[j];
             printf("j back to %d\n",j);
         }
     }
     if(j == strlen(T))
         return i-strlen(T);
     else
         return ;
 }
 int old_index(char * S,char * T){
     int i=;
     int j=;
     while(i<strlen(S) && j<strlen(T)){
         if( S[i] == T[j] ){
             ++i;
             ++j;
         }
         else{
             i = i-j+; //上一次的下一个
             j=;
         }
     }
     if(j == strlen(T))
         return i-strlen(T);
     else
         return -;
 }

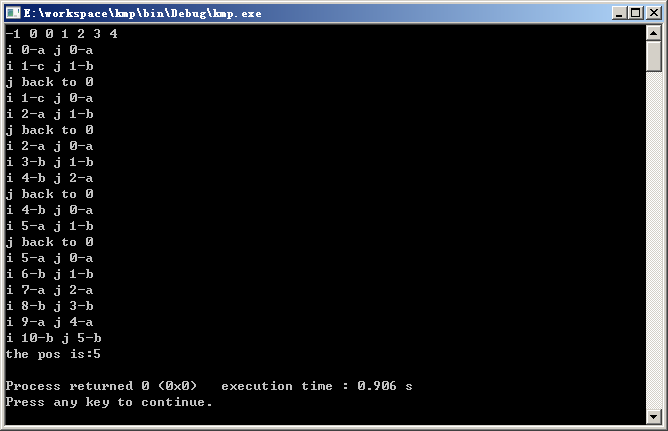
运行结果