Happy Matt Friends（HDU5119 + dp）

题目链接：

　　http://acm.hdu.edu.cn/showproblem.php?pid=5119

题目：

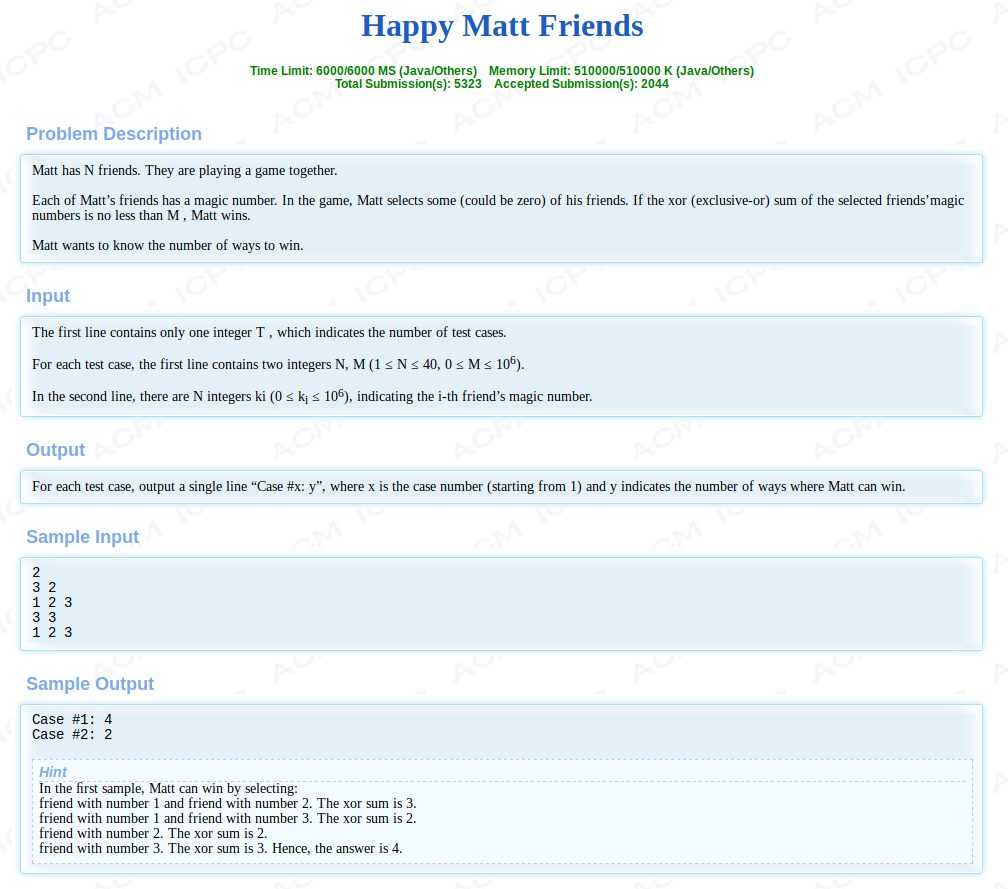
题意：

　　求选择任意个数，使其异或和大于等于m的方案数。

思路：

　　每个数有选和不选两种方案，显然是背包思想。dp[i][j]表示前i个物品异或和为j时的方案数，转移方程为dp[i][j] = dp[i-1][j] + dp[i-1][j^a[i]]。这题可以考虑用滚动数组滚动掉一维，当然了，不滚动也是可以过滴～

代码实现如下：

 #include <set>
 #include <map>
 #include <deque>
 #include <ctime>
 #include <stack>
 #include <cmath>
 #include <queue>
 #include <string>
 #include <cstdio>
 #include <vector>
 #include <iomanip>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pll;
 typedef pair<LL, int> pli;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson rt<<1
 #define rson rt<<1|1
 #define name2str(name)(#name)
 #define bug printf("**********\n");
 #define IO ios::sync_with_stdio(false);
 #define debug(x) cout<<#x<<"=["<<x<<"]"<<endl;
 #define FIN freopen("/home/dillonh/CLionProjects/in.txt","r",stdin);

 const double eps = 1e-;
 const int maxn = (<<) + ;
 const int inf = 0x3f3f3f3f;
 const double pi = acos(-1.0);
 const LL INF = 0x3f3f3f3f3f3f3f3fLL;

 int t, n, m;
 int a[], dp[][maxn];

 int main() {
 #ifndef ONLINE_JUDGE
     FIN;
 #endif
     int icase = ;
     scanf("%d", &t);
     while(t--) {
         scanf("%d%d", &n, &m);
         int mx = , cnt = ;
         for(int i = ; i <= n; i++) scanf("%d", &a[i]), mx = max(mx, a[i]);
         memset(dp, , sizeof(dp));
         dp[][] = ;
         while(mx) cnt++,mx >>= ;
         for(int i = ; i <= n; i++) {
             for(int j = ; j <= (<<cnt); j++) {
                 dp[i&][j] = dp[(i-)&][j] + dp[(i-)&][j^a[i]];
             }
         }
         LL ans = ;
         for(int i = m; i < maxn; i++) ans += dp[n&][i];
         printf("Case #%d: %lld\n", ++icase, ans);
     }
     return ;
 }