洛咕 P3645 [APIO2015]雅加达的摩天楼

暴力连边可以每个bi向i+kdi连边权是k的边。

考虑这样的优化：

然后发现显然是不行的，因为可能还没有走到一个dog的建筑物就走了这个dog的边。

然后就有一个很妙的方法——建一个新的图，和原图分开，这样就没有问题了。

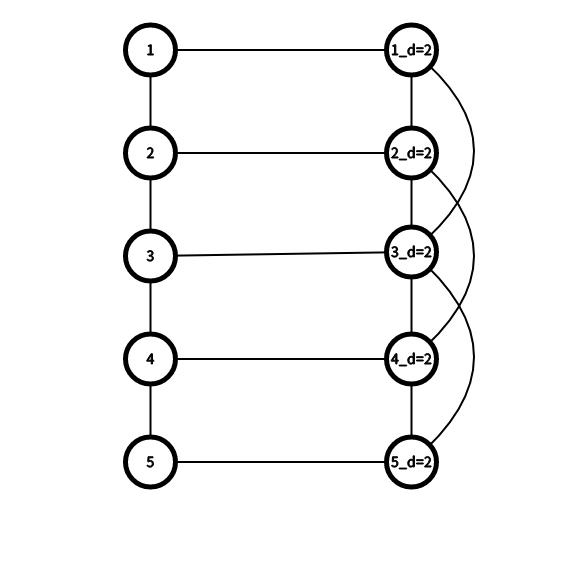
左边这一个是原图，连向原图的点边是可以走的，但是原图的点可以走出去当且仅当这个点上有一个d=目标图d的dog

可以这样建\(\sqrt n\)个图，剩下的图在原图上暴力建，边数都\(<\sqrt n\)

所以最后点数边数都是\(n\sqrt n\)的

注意不用把图建出来，在跑的时候知道了这个点的编号以及d的值就可以了

（代码d=0代表原图）

#include<bits/stdc++.h>
#define il inline
#define vd void
typedef long long ll;
il int gi(){
    int x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return x*f;
}
using std::pair;
using std::make_pair;
int B[30010],P[30010];
std::vector<int>s[30010];
struct point{int x,y;};
#define len 30010*200
pair<int,int>que[len];int hd,tl;
ll dist[30010][200];
bool inq[30010][200];
int main(){
#ifndef ONLINE_JUDGE
    freopen("3645.in","r",stdin);
    freopen("3645.out","w",stdout);
#endif
    int n=gi(),m=gi(),sz=sqrt(n);
    for(int i=1;i<=m;++i)B[i]=gi()+1,P[i]=gi(),s[B[i]].push_back(P[i]);
    memset(dist,63,sizeof dist);
    dist[B[1]][0]=0;que[tl++]=make_pair(B[1],0);inq[B[1]][0]=1;
    while(hd^tl){
        int x=que[hd].first,y=que[hd].second;
#define update(a,b,c) {if(dist[a][b]>dist[x][y]+c){dist[a][b]=dist[x][y]+c;if(!inq[a][b]){inq[a][b]=1,que[tl++]=make_pair(a,b);if(tl==len)tl=0;}}}
        if(y){
            update(x,0,0);
            if(x>y)update(x-y,y,1);
            if(x+y<=n)update(x+y,y,1);
        }else{
            for(int i=0;i<s[x].size();++i)
                if(s[x][i]<=sz)update(x,s[x][i],0)
                else{
                    for(int j=x-s[x][i],k=1;j>0;j-=s[x][i],++k)update(j,0,k);
                    for(int j=x+s[x][i],k=1;j<=n;j+=s[x][i],++k)update(j,0,k);
                }
        }
        ++hd;if(hd==len)hd=0;
        inq[x][y]=0;
    }
    if(dist[B[2]][0]==dist[0][0])puts("-1");
    else printf("%lld\n",dist[B[2]][0]);
    return 0;
}