【刷题】BZOJ 2820 YY的GCD

Description

神犇YY虐完数论后给傻×kAc出了一题给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对kAc这种傻×必然不会了，于是向你来请教……多组输入

Input

第一行一个整数T 表述数据组数接下来T行，每行两个正整数，表示N, M

Output

T行，每行一个整数表示第i组数据的结果

Sample Input

2
10 10
100 100

Sample Output

30
2791

HINT

T = 10000

N, M <= 10000000

Solution

最近开始狂补东西

莫比乌斯反演就是之一，然后做题

个人认为反演里要设计出F(x)和f(x)是有难度的，其他大佬们都说做多了就是套路了，所以还欠火候，加紧做题

对于这道题，我们设F(d)为gcd为d及其倍数的对数的个数，设f(x)为gcd为d的对数的个数

那么我们有

进行反演

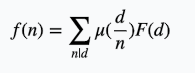
那么需要求的就是（p为质数，小于等于N也小于等于M）

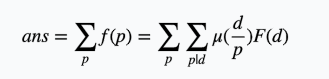
改变枚举顺序，把枚举p的倍数变成枚举上式的d/p

并且因为

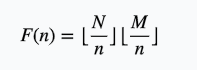
式子变为

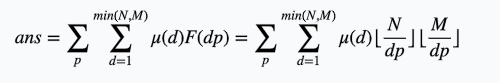
我们令T=dp，把枚举d变为枚举T，同时把后边的两个分式提出来

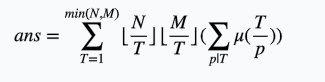
发现后面的可以在素数筛的时候预处理，那么对于一组数据就可做了

对于多组数据，我们发现这个式子是可以整除分块的，优化后就可以过了

对于预处理，我们设一个g(T)

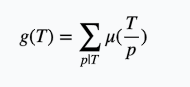
素数筛的时候，令k=i*prime[j]

1）如果prime[j]整除i，mu[k]=0

2）如果不整除，那么根据定义，mu[k]=-mu[i]

因为筛中每个数只会筛到一次，所以赋值之后就不会再被覆盖

由于之前用了整除分块，所以g还需要一个数组s存前缀和，分块时就可以直接把值拿出来了

#include<bits/stdc++.h>
#define ll long long
const int MAXN=+;
ll T,prime[MAXN],cnt,g[MAXN],s[MAXN],mu[MAXN];
bool vis[MAXN];
template<typename T> inline void read(T &x)
{
    T data=,w=;
    char ch=;
    while(ch!='-'&&(ch<''||ch>''))ch=getchar();
    if(ch=='-')w=-,ch=getchar();
    while(ch>=''&&ch<='')data=((T)data<<)+((T)data<<)+(ch^''),ch=getchar();
    x=data*w;
}
template<typename T> inline void write(T x,char c='\0')
{
    if(x<)putchar('-'),x=-x;
    if(x>)write(x/);
    putchar(x%+'');
    if(c!='\0')putchar(c);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline void init()
{
    memset(vis,true,sizeof(vis));
    vis[]=vis[]=;
    mu[]=;
    for(register int i=;i<MAXN;++i)
    {
        if(vis[i])
        {
            prime[++cnt]=i;
            mu[i]=-;
        }
        for(register int j=;j<=cnt&&i*prime[j]<MAXN;++j)
        {
            vis[i*prime[j]]=;
            if(i%prime[j])mu[i*prime[j]]=-mu[i];
            else break;
        }
    }
    for(register int j=;j<=cnt;++j)
        for(register int i=;i*prime[j]<MAXN;++i)g[i*prime[j]]+=mu[i];
    for(register int i=;i<MAXN;++i)s[i]=s[i-]+g[i];
}
inline ll solve(ll N,ll M)
{
    ll ans=;
    for(register int i=;;)
    {
        if(i>min(N,M))break;
        ll j=min(N/(N/i),M/(M/i));
        ans+=(N/i)*(M/i)*(s[j]-s[i-]);
        i=j+;
    }
    return ans;
}
int main()
{
    init();
    read(T);
    while(T--)
    {
        ll N,M;
        read(N);read(M);
        write(solve(N,M),'\n');
    }
    return ;
}

2820 YY的GCD