台哥原创:java 俄罗斯方块源码
大四的时候,用java开发,耗时一周
界面参照当时用的联想手机里的俄罗斯方块

这里的级别,标识难度,1是初级,方块下降速度很慢,5是最高级,下降速度最快
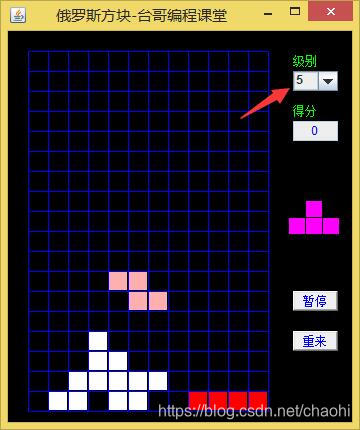
得分:每消除一行,会给10分,同时消除的行数越多,加的分数越大。
界面会提前给出下一个要出现的方块,并且有暂停功能。

俄罗斯方块里是有七种方块类型,比如长条、方块,
我这里的实现方式是定义了一个基础的方块root类,
然后七种方块都继承root
代码片段:
台哥原创:java 俄罗斯方块源码的更多相关文章
- 【转】Java HashMap 源码解析(好文章)
.fluid-width-video-wrapper { width: 100%; position: relative; padding: 0; } .fluid-width-video-wra ...
- 程序兵法:Java String 源码的排序算法(一)
摘要: 原创出处 https://www.bysocket.com 「公众号:泥瓦匠BYSocket 」欢迎关注和转载,保留摘要,谢谢! 这是泥瓦匠的第103篇原创 <程序兵法:Java Str ...
- java集合源码分析(三):ArrayList
概述 在前文:java集合源码分析(二):List与AbstractList 和 java集合源码分析(一):Collection 与 AbstractCollection 中,我们大致了解了从 Co ...
- Java集合源码分析(四)Vector<E>
Vector<E>简介 Vector也是基于数组实现的,是一个动态数组,其容量能自动增长. Vector是JDK1.0引入了,它的很多实现方法都加入了同步语句,因此是线程安全的(其实也只是 ...
- Java集合源码分析(三)LinkedList
LinkedList简介 LinkedList是基于双向循环链表(从源码中可以很容易看出)实现的,除了可以当做链表来操作外,它还可以当做栈.队列和双端队列来使用. LinkedList同样是非线程安全 ...
- Java集合源码分析(二)ArrayList
ArrayList简介 ArrayList是基于数组实现的,是一个动态数组,其容量能自动增长,类似于C语言中的动态申请内存,动态增长内存. ArrayList不是线程安全的,只能用在单线程环境下,多线 ...
- Java集合源码学习(一)集合框架概览
>>集合框架 Java集合框架包含了大部分Java开发中用到的数据结构,主要包括List列表.Set集合.Map映射.迭代器(Iterator.Enumeration).工具类(Array ...
- 编译哈工大语言技术平台云LTP(C++)源码及LTP4J(Java)源码
转自:编译哈工大语言技术平台云LTP(C++)源码及LTP4J(Java)源码 JDK:java version “1.8.0_31”Java(TM) SE Runtime Environment ( ...
- Java Reference 源码分析
@(Java)[Reference] Java Reference 源码分析 Reference对象封装了其它对象的引用,可以和普通的对象一样操作,在一定的限制条件下,支持和垃圾收集器的交互.即可以使 ...
随机推荐
- 使用K近邻算法改进约会网站的配对效果
1 定义数据集导入函数 import numpy as np """ 函数说明:打开并解析文件,对数据进行分类:1 代表不喜欢,2 代表魅力一般,3 代表极具魅力 Par ...
- Spring IoC,IoC原理
一.IoC概念及原理 IOC的别名:依赖注入(DI) 2004年,Martin Fowler探讨了同一个问题,既然IOC是控制反转,那么到底是“哪些方面的控制被反转了呢?”,经过详细地分析和论证后,他 ...
- mysql数据库监控工具-MONyog的配置和基本使用项
测试数据传输前,研发要求需要监控10万,50万,100万数量级的数据在传输过程数据库服务器的资源消耗情况,因为数据传输服务是定时任务执行,配置10秒中一次,一次处理500条,处理完10万数据可能要半个 ...
- 五分钟搞懂 Linux 重点知识,傻瓜都能学会!
来源:无痴迷,不成功 www.cnblogs.com/justmine/p/9053419.html 写在前面 我们都知道Linux是一个支持多用户.多任务的系统,这也是它最优秀的特性,即可能同时有很 ...
- C89标准和C99标准C11标准的区别
转载 C89标准和C99标准C11标准的区别 C99对C89的改变 1.增加restrict指针 C99中增加了公适用于指针的restrict类型修饰符,它是初始访问指针所指对象的惟一途径,因此只有借 ...
- poj1305 Fermat vs. Pythagoras(勾股数)
题目传送门 题意: 设不定方程:x^2+y^2=z^2若正整数三元组(x,y,z)满足上述方程,则称为毕达哥拉斯三元组.若gcd(x,y,z)=1,则称为本原的毕达哥拉斯三元组. 定理:正整数x,y, ...
- bzoj3188 [Coci 2011]Upit(分块)
Time Limit: 10 Sec Memory Limit: 128 MB Description 你需要维护一个序列,支持以下4种操作.一,将区间(u,v)的数覆盖为C:二,将区间(u,v)的 ...
- 在navcat中清空数据后,设置id归零方法
写后台完成后,需要清空Mysql数据库中的测试数据,但是后面新增的数据,一直是以原来所删除数据的最大id为增量基本,比如,对于一些id敏感的项,十分不便,如图 原有10条数据,清空后,新增一两条,手动 ...
- Latex--入门系列一
Latex 专业的参考 tex对于论文写作或者其他的一些需要排版的写作来说,还是非常有意义的.我在网上看到这个对于Latex的入门介绍还是比较全面的,Arbitrary reference .所以将会 ...
- 装饰器模式-Decerator
一.定义 装饰器模式又叫做包装模式(Wrapper).装饰器模式以对客户端透明的方式扩展对象的功能,是继承关系的一个替代方案. 在以下情况下应该使用装饰器模式: 1.需要扩展一个类的功能,或给一个类增 ...
