机器学习四 SVM

引言
SVM
线性可分SVM
线性不可分SVM
Hinge Loss
非线性SVM
- 核函数
总结
参考文献

引言

在深度神经网终(Deep Neural Network, DNN) 大热之前, 在机器学习里有个明星算法就是今天要与大家分享的 支持向量机(Support Vector Machine, SVM). 它是昔日的明星, 虽然现在没有DNN风光, 但它依然是机器学习领域内耀眼的存在, 这当然取决于其强大的学习能力.

第一次听到SVM想必大家跟我一样,这是什么东西,这个'高大上'的名字? support vector? 科技感十足啊~,别急, 等真正了解它了,你就知道其为什么会有这样的名字了.

来看下面的例子:

这有两种类别的数据,class1 与class2, 要把这两类分开, 人类一看就知道在这两类别之间画条直线即可, 比如图上的直线, 正好可以把两类数据完美的分开!,但计算机可不知道如何, 而SVM的作用就是告诉计算机, 如何找到这样一条线,并且找到''某种意义''(别急, 一会就知道是何种意义)上最好的一条线!

这也就是SVM的基本思想: 找到这样一条'线'(在二维数据上,恰如图上展示,为一条线, 如果是三维的, 就成为平面了,如果更高维则称之为 '超平面'(hyperplane) ), 使得数据可以区分. Nothing mysterious~

那''支持向量''是如何来的呢? 这就涉及到SVM是如何找到这样的''最好的''超平面的.

SVM

再看第一张图, 很容易就可智道, 想要区分两类数据, 这样的线可有无数条, 只要位于两类数据之间即可.

然而, 我们的目的(或者说机器学习的目的) 不是或者说不只是为了区分现有的两类数据, 我们真正想要达到的目的是: 当模型在现有数据训练完成后, 将其应用到新的(同种)数据时,我们仍然可以很好的区分两类数据,达到预期的分类效果. 说得专业一点,即 泛化(generalization) 能力.

当有了泛化要求后, 自然地考虑到, 在这无数条可区他两类数据的线中,并不是都合适的, 而且有理由相信, 从泛化的角度讲,肯定存在一条线是这无数条线中泛化能力最好. SVM 要找的就是这条线!

那如何来量化泛化能力呢? 再来看下这张图:

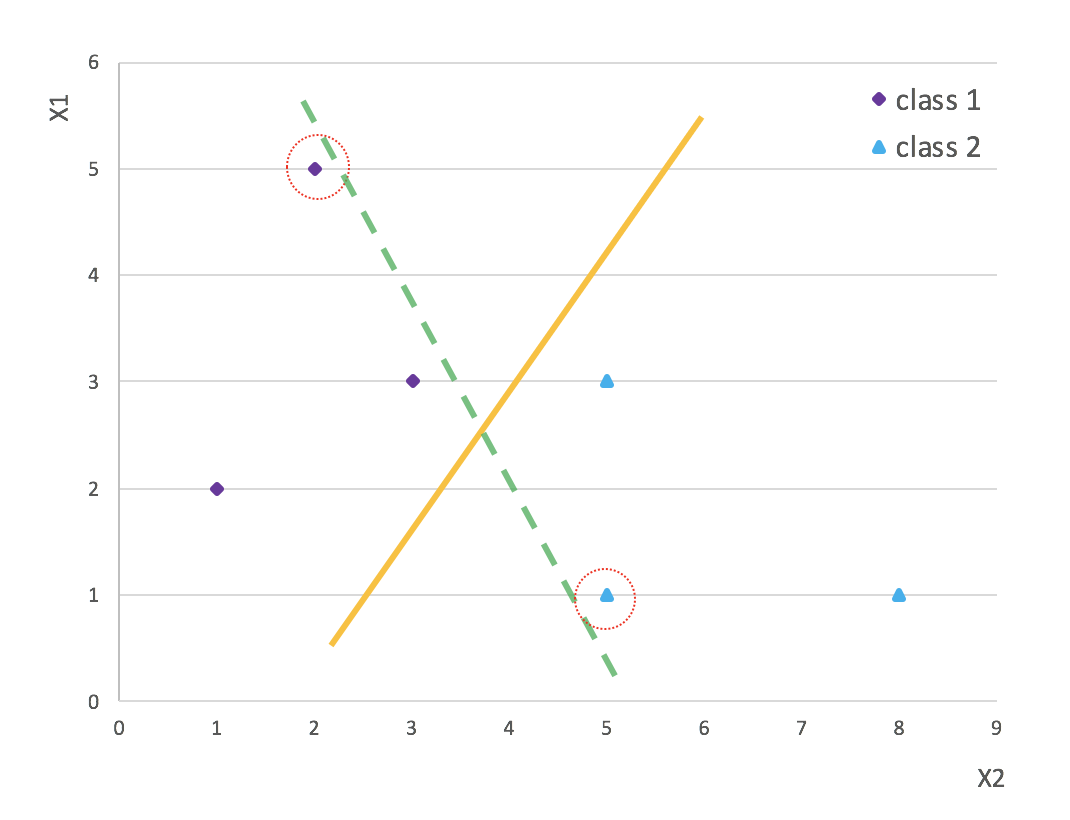
有两条线, 都可以区分两类数据, 从泛化的角度讲,哪个更好呢? 你会发现虚线距离数据更近些(红圈圈出的数据). 这也意味着,如果新数据(或者称为测试数据) 在红圈部位稍微有一点偏差,就会越过虚线,从而导致虚线的分类准确度下降甚至失败.

相较之下,实线距离数据的位置较远, 新数据的到来时, 实线对数据的波动的容忍度就大些, 即实线的泛化能力更强些.

这样我们智道了模型的泛化能力可以用与数据间的距离来量化. 距离越化,泛化能力越强, 距离最大的,泛化能力也是最强的. 因此要找到泛化能力最强的,等价于找到与数据距离最大的超平面.

量衡量一条直线与数据间的距离,想必就算我不用红圈圈出,你也会下意识地关注离直线最近的数据点与直线的距离, 而其他较远的点,你则没有过多关注,甚至下意识的忽略了, 嘿嘿, 这是完全正确的, 也就是说, 决定超平面也数据距离的就是与超平面距离最近的数据, 换句话说, 影响模型泛化能力的,就是这些距离最近的点.

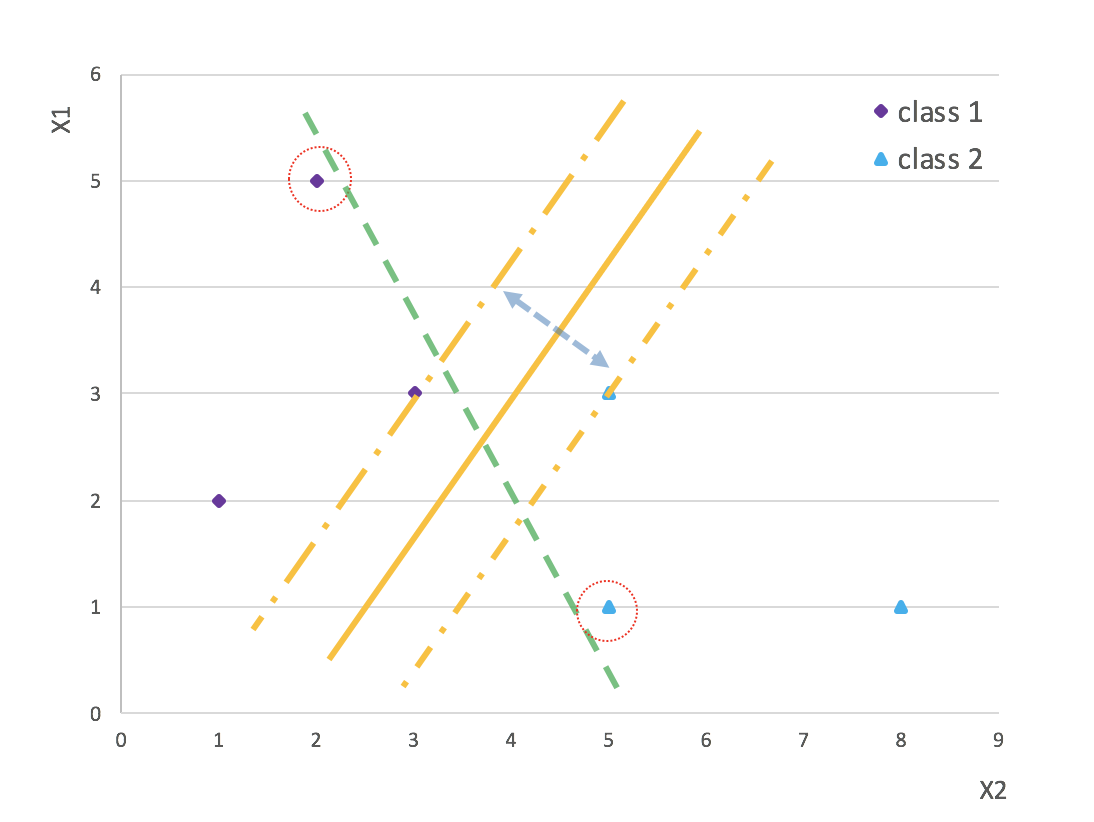
换种角度, 找离最近的点距离最大的超平面, 可以转化为找到边缘间隔(实线两边虚线间的距离)最大的超平面, 如果找到最大间隔,那间隔正中间的位置就是我们梦寐以求的分隔超平面.

你会发现分隔边缘正好是经过最近数据点的超平面. 反过来说(一种比喻), 最近数据点就是支撑点一样, 支撑(或支持)着分隔边缘. 而此类数据点(向量)正是决定模型(或者说分隔超平面)的关键所在. 这样,你就知道SVM为什么用支持向量平命名了.

线性可分SVM

从上面的解释大家应该明白什么是SVM, 它要干什么,它要怎么做等等.

首先,最大边缘超平面是咱们要找的模型, 因此,先描述下超平面, 在空间中,超平面可表示如下:
\[
w^T x + b = 0
\]
其中三个元素均为向量, 可将超平面简记为(w,b). 则样本空间中的数据点到此超平面的距离就可表示为:
\[
r = \frac{|w^Tx+b|}{||w||}
\]
由中学知识我们就可知道, 在超平面的上点, 会满足(1)式, 而在超平面之上的点,则会使 wx + b > 0 (比如上图中方点之于实线); 在超平面之下的点,会使 wx + b < 0 (三角点之于实线). 那不妨设(算是一个trick):
\[
\left\{
\begin{array}\\
y = 1, \qquad wx +b >0;\\
y = -1, \qquad wx + b< 0.
\end{array}
\right.
\]
其中y 表示类别, 则(2)式可改写为:
\[
r = \frac{y(wx+b)}{||w||}
\]
通过(4)式,我们就可将超平面定位于两类之间. 如前所述, 衡量其泛化能力, 通过其与数据样本空间的距离, 而距离的衡量则与支持向量有关了, 超平面与支持向量的距离:
\[
\hat{r}= \min_{x} r
\]
即在样本空间找到与超平面距离最近的点, 而此类点距超平面的距离即为超平面的'泛化能力'.

我们知道满足(4)式的超平面的数量是无数的, 哪一个是最优的呢? 当然是泛化能力最强的了,即:
\[
h = \max_{w,b}\hat{r} = \max_{w,b}\min_{x} \frac{y(wx+b)}{||w||}
\]
其中h 表示最优超平面.

注意这里又有一个trick了, wx + b = 0 表示空间中某一超平面,你会发现 w, b 同时放大或缩小相同的倍数, 即 \(a ( wx + b ) = w'x+b'= 0 (a> 0)\), 超平面是没有变化的, 同理
\[
h = \max_{w,b}\min_{x} \frac{y(wx+b)}{||w||} = \max_{w,b}\min_{x} \frac{y a(wx+b)}{||a w||}
\]
因此,不妨调整 a 使得 \(y a( wx +b) = 1\), 于是:
\[
h = \max_{w,b} \frac{1}{||w'||} \\ s.t \quad y(w'x+b')\ge 1.
\]
其中 \(w' = aw, b' = ab\), 因为w,b 在上式是是变量,且可同时放大或缩小, 为下面简便, 在符号上直接用 w 替代 w', b 替代 b'.

于是上式可简记为:
\[
h = \max_{w,b} \frac{1}{||w||} \\ s.t \quad y(wx+b)\ge 1.
\]
对 (9)式的优化,即求 \(\frac{1}{||w||}\) 最大化可转化为其对偶问题:最小化 \(\frac{1}{2}||w||^2\) . (\(\frac{1}{2}\)的出现有的参考书说是因为距离是超平面两个缘都要满足, 即要最大化 \(\frac{2}{||w||}\), 更多的是直接不提, 还有一种说法是为了方便后面的运算,比如求偏导. 我倾向于最后一种说法).

再根据Lagrange 乘子(multiplier)法:
\[
L(w,b, \alpha) = \frac{1}{2}||w||^2 + \sum_{i = 1}^N \alpha_i(1 - y_i (wx_i +b))
\]
其中\(1 \le i\le n,\quad \alpha \ge 0\), n 为样本量. 对w,b 求偏导即可得到:
\[
w = \sum_{i = 1}^{n} \alpha_i y_i x_i \\
0 = \sum_{i=1}^n \alpha_i y_i
\]
将(11)式代入(10)式, 即可得到(9)式的对偶问题:
\[
\begin{array}\\
\max_{\alpha} \sum_{i = 1}^{n}\alpha_i - \frac{1}{2}\sum_{i = 1}^n\sum_{j =1}^n \alpha_i\alpha_jy_iy_j(x^T_ix_j)\\
s.t. \qquad \sum_{i = 1}^n \alpha_iy_i = 0, \\
\qquad \qquad\alpha_i\ge 0, i = 1,2,\dots,n.
\end{array}
\]
注意这里有个转变: \(L(w,b,\alpha)\)的最小化是通过(w, b), 而其对偶问题是max, 通过\(\alpha\). 至于为何会变成 max, 一个直观的解释是 (12)式中,的\(x^Tx\) 是二次式, 其前面有负号, 只有最大值, 而没有最小值.

对于(12)式的求解应用到一种叫做 Sequential Minimal Optimization(SMO)的算法,其基本思想是每次选择两个变量 \(\alpha_i, \alpha_j\), 并固定其他所有参数, 然后再求解,循环此过程,直到收敛.

线性不可分SVM

上面展示的是最理想的状态, 即两类数据泾渭分明, 生产实践中可没有那么幸运, 数据往不是一条线就能分开的,比如下面的图:

在两边缘之间还有数据点散落,如果我们一定要找一条区分两种类别的线似不可能了, 而且也完全没必要. 因为就算找到,那这条线也一定会距离数据很近,也就是说泛化能力一定很弱(过拟合 Overfitting). 莫不如,在训练时,允许超平面有一定的错误率, 即允许少量数据点跑到两边缘间隔之间.这样妥协的好处就是我们还会找到边缘间隔相对较大的超平面, 因此在测试数据上会有更好的表现. 我们把这样的间隔称为soft margin.

soft margin 也就意味着:
\[
y_i (wx_i + b) \ge 1 - \xi_i, \qquad \xi_i \ge 0
\]
其中的\(\xi_i\) 称之为松弛变量(slack value) , 优化函数也相应的变成:
\[
\min_{w,b} \frac{1}{2} ||w|| + C\sum_{ji = 1}^n \xi_{i}
\]
其中参数 C >0 称为惩罚参数(penalized parameter). 相像一下,当 C 非常大时, 为了最小化(14)式, \(\xi_i\) 一定要尽可能的小才好, 也就说(13)式更加接近(9)式的约束条件, 也就是soft margin 会越来越harder, 也就是更趋于线性可分. 类似地, C 很小, 那 \(\xi_i\) 适当的变大也没有在这大的影响,也是就说soft margin 更加的 softer, 也就是说margin 允许更好的数据进入到margins 之间.

解法如上:
\[
L(w, b ,\alpha,\xi,u) = \frac{1}{2} ||w|| + C\sum_{ji = 1}^n \xi_{i}+ \sum_{i =1}^n \alpha_i(1 - \xi_i-y_i (wx_i + b) ) + u_i \xi_i
\]
对\(w, b, \xi\) 求偏导:
\[
w = \sum_{i = 1}^n \alpha_iy_ix_i\\
0 = \sum_{i = 1}^n \alpha_i y_i\\
C = \alpha_i +\mu_i
\]
带入(15)式就可得到其对偶问题:
\[
\begin{array}\\
\max_{\alpha} \sum_{i = 1}^{n}\alpha_i - \frac{1}{2}\sum_{i = 1}^n\sum_{j =1}^n \alpha_i\alpha_jy_iy_j(x^T_ix_j)\\
s.t. \qquad \sum_{i = 1}^n \alpha_iy_i = 0, \\
\qquad \qquad 0\le \alpha_i\le C,\quad i = 1,2,\dots,n.
\end{array}
\]
你会发现, (17) 式与(12)式有唯一差别即是 \(\alpha_i\) 的限制条件.

Hinge Loss

线性SVM 还有另外一种解释: 我们的目的是尽可能的区分两类数据, 也就是说分错的数据要尽可能的少, 也即在两边缘边隔内的数据越少越好, 注意这里所说的''越少越好''的前提是最小边缘确定了的(即调整w, b 使 wx +b = 1,),否则正如前面所说,找到的超平面可能泛化能力很弱.

也就是说, 我们要关注\(wx+b \le 1\) 的数据点, 而\(wx+b > 1\) 则不需要关注, 因这些是一定不会分错的点(因为这些数据距离超平面大于最小距离啊).

因此损失函数可以这样写:
\[
Loss = \sum_{i=1}^n (1 - (wx +b))_{+} + \lambda ||w||^2
\]
优化函数即为:
\[
\min Loss = min \sum_{i=1}^n (1 - (wx +b))_{+} + \lambda ||w||^2
\]
其正第一项下标'+' 表示\((z)_+ = \max(0, z)\), 第二项现在就变成了正则项. (19)式等价于(13, 14)式.最终的对偶问题也是(17)式.

非线性SVM

有时(很多时候)数据并能用一条线区分开, 就算你考虑soft margin, 就算你考虑slack varibles, 还是不行,比如下图:

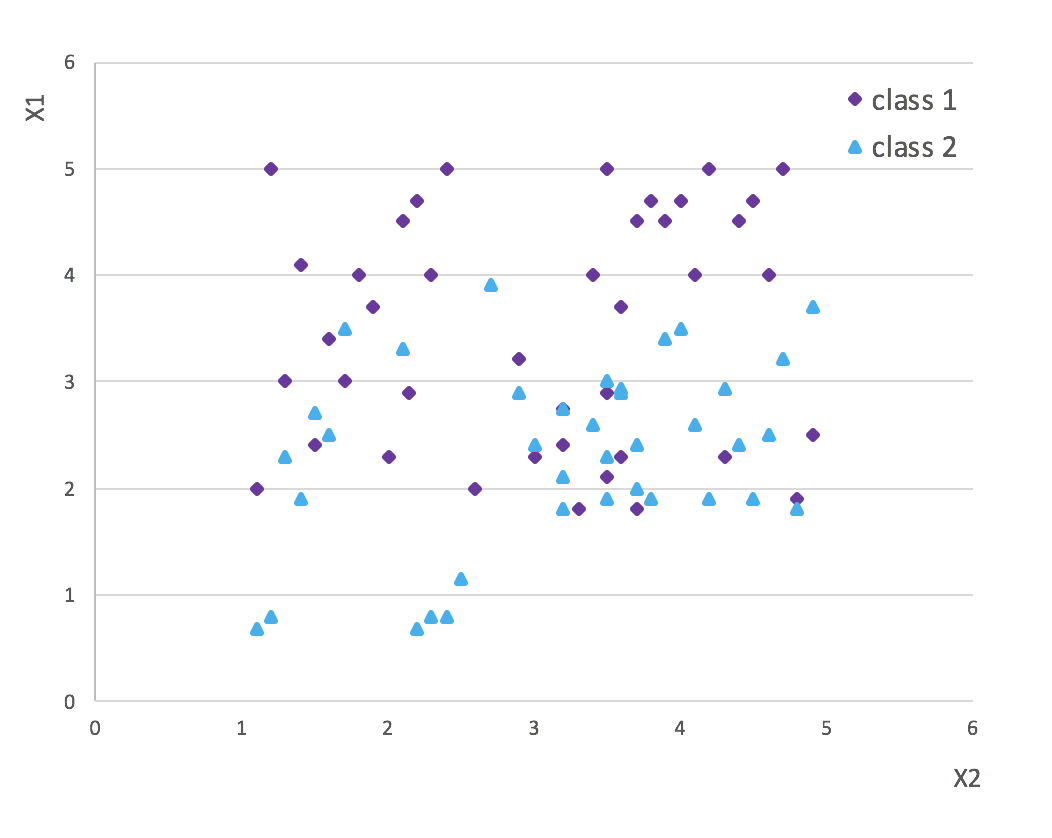
我们很难在平面上划一条线可以很好的(误差率可接受的)区分两类数据. 这时介绍另一个trick了— 核函数(kernel function).

再次明确我们的目的: 我们要很好的区分两类数据. 现在我们可以换一种思路,来看下张图:

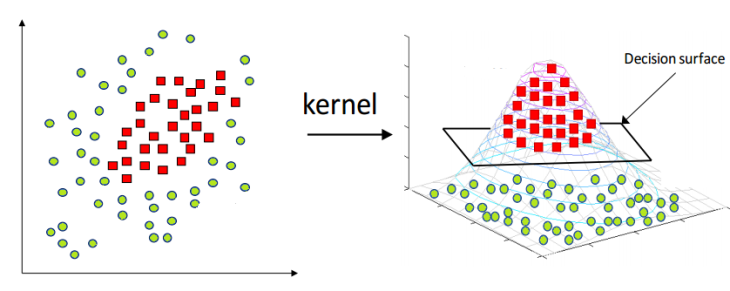
(图片来源于网络)

左图很明显没有一条直线可以分开两类数据, 但我们可以考虑,左图是张三维图片的俯视图, 如果我们通过某种方法将其还原成三维形态,那很明显(右图) 就可以找到一个超平面将两类数据完美区分了. 这种方法就是核函数. 上面的思路已经清晰:通过数据升维的手段,找到一个超平面将数据分开.

说得专业些,上面的思想即是通过变换(一般为非线性变换), 将原空间(输入空间)(欧氏空间\(R^n\) 或离散集合)映射到新空间(特征空间)(希尔伯特空间H), 使得原空间超曲面模型对应于特征空间的超平面. 从而完成分类任务.

核函数

核函数: 设 X 是输入空间, H 为特征空间, 如果存在一个从 X 到 H 的映射:
\[
\phi(x) : X \rightarrow H
\]
使得对所有\(x_i, x_j \in X\), 函数 K(x_i,x_j)满足:
\[
\kappa(x,x_j) = \phi(x)\cdot \phi(x_j)
\]
则称 K(x, x_j) 为核函数, \(\phi(x)\) 为映射函数.

改写(12)式((17)式也是类似的,因二者只差个约束 C.):
\[
\begin{array}\\
\max_{\alpha} \sum_{i = 1}^{n}\alpha_i - \frac{1}{2}\sum_{i = 1}^n\sum_{j =1}^n \alpha_i\alpha_jy_iy_j(\phi(x^T_i)\phi(x_j))\\
=\max_{\alpha} \sum_{i = 1}^{n}\alpha_i - \frac{1}{2}\sum_{i = 1}^n\sum_{j =1}^n \alpha_i\alpha_jy_iy_j \kappa(x^T_i,x_j)\\
s.t. \qquad \sum_{i = 1}^n \alpha_iy_i = 0, \\
\qquad \qquad\alpha_i\ge 0, i = 1,2,\dots,n.
\end{array}
\]
通常我们并不知道映射函数是什么, 而且大多数情况下映射函数的维度会比原来高出很多, 计算复杂且会造成维灾难(dimension curse). 因此我们才会考虑核函数替代映射函数的内积(\(\phi(x)\cdot \phi(z)\)).

至于如找核函数, 会涉及正定核, mercer 定理等,不就展开讨论了.

下面列几个常用的核函数:

多项式核函数:
\[
\kappa(x,z) = (x_i \cdot x_j+1)^p
\]
高斯核函数(也称径向基核函数):
\[
\kappa(x_i,x_j = \exp(-\frac{||x_i-x_j||^2}{2\sigma^2})
\]
拉普拉斯核函数:
\[
\kappa(x_i,x_j) = \exp(-\frac{||x_i-x_j||}{\sigma})
\]
Sigmoid 核函数:
\[
\kappa(x_i,x_j) = \tanh(\beta x_i^T\cdot x_j + \theta),\qquad \beta> 0, \theta <0.
\]

总结

对SVM, 要记住的点: 名字由来, trick1 ( 将两类数据分成正负两类: +1, -1); trick 2 ( 对于支持向量: wx + b = 1); trick3( 对偶问题: 极大变极小等); trick 4 soft margin and slack varible; trick 5 hinge loss ( svm 优化函数的另外一种解释); trick 6 (kernel function, 维灾难).

参考文献

机器学习, 周志华, 2016, 清华大学出版社;
统计学习方法, 李航, 2012, 清华大学出版社;
数据挖掘:概念与技术, JiaWei han et al 著, 范明等译, 2012, 机械工业出版社;
数据挖掘导论, Pang-Ning Tan et al 著, 范明等译, 2011, 人民邮电出版社;
Pattern Recognition and Machine Learning,2006, Christopher M. Bishop, Springer.