HDU 6631 line symmetric（枚举）

首先能想到的是至少有一对相邻点或者中间间隔一个点的点对满足轴对称，那么接下来只需要枚举剩下的点对是否满足至多移动一个点可以满足要求。

第一种情况，对于所有点对都满足要求，那么Yes。

第二种情况，有一个点不满足要求，那么显然这种情况只可能是奇数点的时候才出现，那么只需要将这个点移到对称轴上则满足要求，那么Yes。

第三种情况，有两个点不满足要求，然后我们需要枚举这两个点对应的对称点是否满足要求，对于其中一个点的对称点判断他是否和之前所有点重合，以及判断这个点是否在对称轴上。

这样还不够，还需要考虑对于对称轴两边的可能的对应的对称点，他们是不是在对应一侧，如果两个点都不在对应的一侧，说明这两个点自交，则不能满足要求，直接跳过。

多注意细节吧，现场wa到自闭。

数据：

5
-100 -100
0 0
-100 100
2 -1
100 1
N

7
-3 3
-5 -5
1 -3
-1 -3
0 2
5 -5
3 3
N

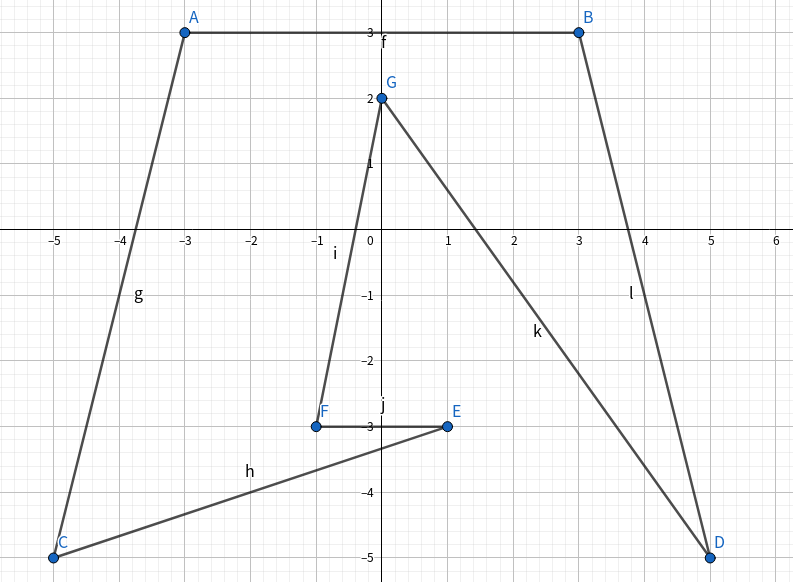
附图说明：

 //        ——By DD_BOND

 //#include<bits/stdc++.h>
 //#include<unordered_map>
 //#include<unordered_set>
 #include<functional>
 #include<algorithm>
 #include<iostream>
 //#include<ext/rope>
 #include<iomanip>
 #include<climits>
 #include<cstring>
 #include<cstdlib>
 #include<cstddef>
 #include<cstdio>
 #include<memory>
 #include<vector>
 #include<cctype>
 #include<string>
 #include<cmath>
 #include<queue>
 #include<deque>
 #include<ctime>
 #include<stack>
 #include<map>
 #include<set>

 #define fi first
 #define se second
 #define MP make_pair
 #define pb push_back

 typedef long long ll;

 using namespace std;

 const int MAXN=1e3+;
 const double eps=1e-;
 const double pi=acos(-1.0);
 const ll INF=0x3f3f3f3f3f3f3f3f;

 inline int dcmp(double x){
     if(fabs(x)<eps)    return ;
     return (x>? : -);
 }

 inline double sqr(double x){ return x*x; }

 struct Point{
     double x,y;
     Point(){ x=,y=; }
     Point(double _x,double _y):x(_x),y(_y){}
     void input(){ scanf("%lf%lf",&x,&y); }
     bool operator ==(const Point &b)const{
         return (dcmp(x-b.x)==&&dcmp(y-b.y)==);
     }
     Point operator +(const Point &b)const{
         return Point(x+b.x,y+b.y);
     }
     Point operator -(const Point &b)const{
         return Point(x-b.x,y-b.y);
     }
     Point operator *(double a){
         return Point(x*a,y*a);
     }
     Point operator /(double a){
         return Point(x/a,y/a);
     }
     double len2(){    //长度平方
         return sqr(x)+sqr(y);
     }
     Point rotate_left(){    //逆时针旋转90度
         return Point(-y,x);
     }
 };

 inline double cross(Point a,Point b){    //叉积
     return a.x*b.y-a.y*b.x;
 }

 inline double dot(Point a,Point b){    //点积
     return a.x*b.x+a.y*b.y;
 }

 struct Line{
     Point s,e;
     Line(){}
     Line(Point _s,Point _e):s(_s),e(_e){} //两点确定直线
 };

 int relation(Point p,Line l){    //点和向量关系   1:左侧   2:右侧   3:在线上
     int c=dcmp(cross(p-l.s,l.e-l.s));
     if(c<)    return ;
     else if(c>)    return ;
     else    return ;
 }

 Point projection(Point p,Line a){        //点在直线上的投影
     return a.s+(((a.e-a.s)*dot(a.e-a.s,p-a.s))/(a.e-a.s).len2());
 }

 Point symmetry(Point p,Line a){            //点关于直线的对称点
     Point q=projection(p,a);
     return Point(*q.x-p.x,*q.y-p.y);
 }

 int vis[MAXN];
 vector<Line>st;
 Point point[MAXN];

 int main(void){
     int T;  scanf("%d",&T);
     while(T--){
         int n,ans=;  scanf("%d",&n);
         for(int i=;i<n;i++)    point[i].input();
         for(int i=;i<n&&!ans;i++){
             int s=i,t=(i+)%n;
             Point mid=(point[s]+point[t])/,vec=(point[s]-point[t]).rotate_left();
             Line line(mid,mid+vec);
             int num=,error=;
             memset(vis,,sizeof(vis));
             while(!vis[s]&&!vis[t]){
                 vis[s]=,vis[t]=;
                 Point p1=(point[s]+point[t])/,dir=(point[s]-point[t]).rotate_left();
                 Point p2=p1+dir;
                 if(dcmp(cross(point[i]-mid,vec))*dcmp(cross(point[s]-mid,vec))<&&dcmp(cross(point[(i+)%n]-mid,vec))*dcmp(cross(point[t]-mid,vec))<)   error=;
                 if(relation(p1,line)==&&relation(p2,line)==){
                     if(s!=t)    num+=;
                     else    num++;
                 }
                 s=(s-+n)%n,t=(t+)%n;
             }
             if(error)   continue;
             if(num+>=n)  ans=;
             else if(num+==n){
                 s=i,t=(i+)%n;
                 memset(vis,,sizeof(vis));
                 while(!vis[s]&&!vis[t]){
                     vis[s]=,vis[t]=;
                     Point p1=(point[s]+point[t])/,vec=(point[s]-point[t]).rotate_left();
                     Point p2=p1+vec;
                     if(relation(p1,line)!=||relation(p2,line)!=){
                         if(relation(point[s],line)!=&&relation(point[t],line)!=){
                             int f1=,f2=;
                             Point s1=symmetry(point[s],line),s2=symmetry(point[t],line);
                             for(int j=;j<n;j++)
                                 if(point[j]==s1)
                                     f1=;
                             for(int j=;j<n;j++)
                                 if(point[j]==s2)
                                     f2=;
                             if(!f2||!f1) ans=;
                         }
                         break;
                     }
                     s=(s-+n)%n,t=(t+)%n;
                 }
             }
         }
         for(int i=;i<n&&!ans;i++){
             int s=(i-+n)%n,t=(i+)%n;
             Point mid=(point[s]+point[t])/,vec=(point[s]-point[t]).rotate_left();
             Line line(mid,mid+vec);
             int num=,error=;  s=t=i;
             memset(vis,,sizeof(vis));
             while(!vis[s]&&!vis[t]){
                 vis[s]=,vis[t]=;
                 Point p1=(point[s]+point[t])/,dir=(point[s]-point[t]).rotate_left();
                 Point p2=p1+dir;
                 if(dcmp(cross(point[(i-+n)%n]-mid,vec))*dcmp(cross(point[s]-mid,vec))<&&dcmp(cross(point[(i+)%n]-mid,vec))*dcmp(cross(point[t]-mid,vec))<)   error=;
                 if(relation(p1,line)==&&relation(p2,line)==){
                     if(s!=t)    num+=;
                     else    num++;
                 }
                 s=(s-+n)%n,t=(t+)%n;
             }
             if(error)   continue;
             if(num+>=n)  ans=;
             else if(num+==n){
                 s=t=i;
                 memset(vis,,sizeof(vis));
                 while(!vis[s]&&!vis[t]){
                     vis[s]=,vis[t]=;
                     Point p1=(point[s]+point[t])/,vec=(point[s]-point[t]).rotate_left();
                     Point p2=p1+vec;
                     if(relation(p1,line)!=||relation(p2,line)!=){
                         if(relation(point[s],line)!=&&relation(point[t],line)!=){
                             int f1=,f2=;
                             Point s1=symmetry(point[s],line),s2=symmetry(point[t],line);
                             for(int j=;j<n;j++)
                                 if(point[j]==s1)
                                     f1=;
                             for(int j=;j<n;j++)
                                 if(point[j]==s2)
                                     f2=;
                             if(!f2||!f1) ans=;
                         }
                         break;
                     }
                     s=(s-+n)%n,t=(t+)%n;
                 }
             }
         }
         if(ans) puts("Y");
         else    puts("N");
     }
     return ;
 }