CF613A：Peter and Snow Blower

用一个圆心在(x,y)的圆环覆盖一个n边形，顺或逆时针给出n边形所有顶点，求圆环最小面积。

卡了好久，各种傻逼错误。。

题目就是让我们固定一大一小两个边界圆，我们来看看这两个圆满足什么条件。

首先外面的那个圆肯定是经过n边形的某个顶点，所以外圆半径就是最大的点距。

其次内圆呢，可能经过一个点，也可能与某条边相切，但注意，这里的线是线段不是直线！

所以可能会出现最后的内圆和某条“直线”相交而与其对应的线段没有交点。例如：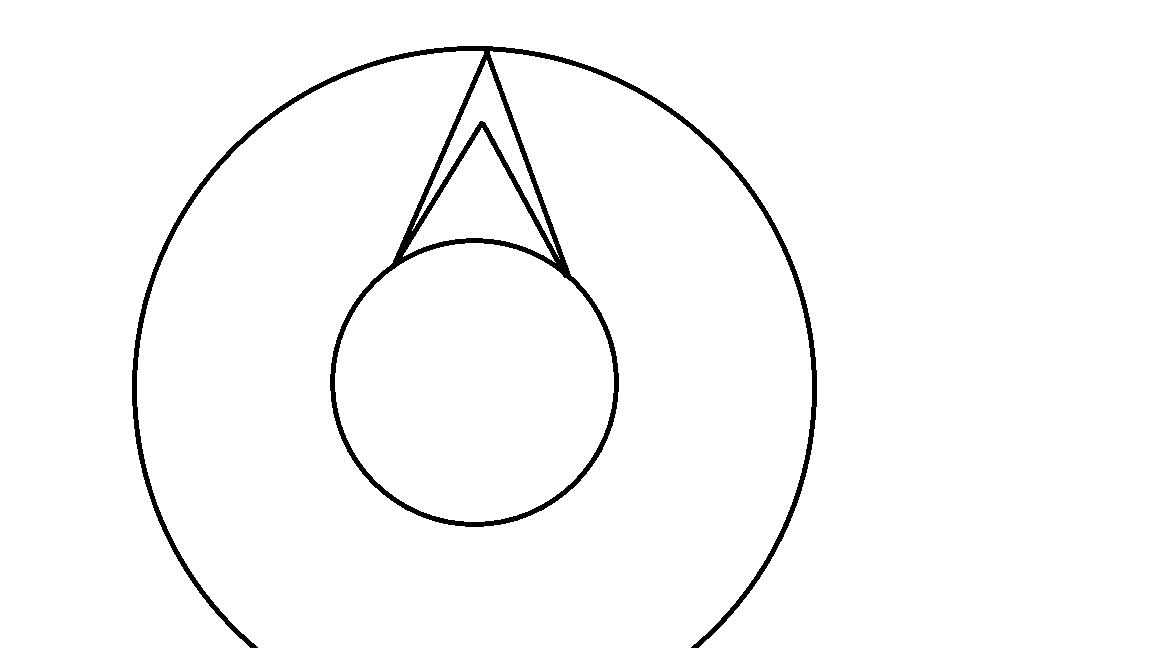

上图中内圆与四条“直线”都相交，但与“线段”只有一个交点。

为了判断内圆，我用了最粗暴的方法--二分，计算与当前半径的圆相交的“直线“的两个交点是否在“线段”上，用横坐标或纵坐标判断。

Trick:

如果是用y=kx+b就会wa，因为平面上不是所有的直线都能这么表示，要用一般式Ax+By+C=0。

计算圆与直线相交情况时记得分B是否为0的情况。所有计算过程中记得判断除0情况。

精度。二分时在精度那里要注意R-eps或者L+eps，不然可能tle。

 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstdlib>
 #include<cstring>
 #include<cmath>
 //#include<iostream>
 using namespace std;

 int n;
 #define maxn 100011
 struct Point
 {
     double x,y;
 }a[maxn],P;
 struct Line
 {
     double a,b,c,dis;
 }l[maxn];
 const double eps=1e-,pi=3.1415926535897932384626434;
 void do_line(int id,double x1,double y1,double x2,double y2)
 {
     if (x1==x2)
     {
         l[id].a=;
         l[id].b=;
         l[id].c=-x1;
     }
     else if (y1==y2)
     {
         l[id].a=;
         l[id].b=;
         l[id].c=-y1;
     }
     else if (x2*y1==x1*y2)
     {
         l[id].c=;
         l[id].a=;
         if (y1) l[id].b=-x1/y1*l[id].a;
         else l[id].b=-x2/y2*l[id].a;
     }
     else
     {
         l[id].c=;
         l[id].a=l[id].c*(y2-y1)/(x2*y1-x1*y2);
         l[id].b=l[id].c*(x2-x1)/(y2*x1-y1*x2);
     }
     l[id].dis=abs(l[id].a*P.x+l[id].b*P.y+l[id].c)/sqrt(l[id].a*l[id].a+l[id].b*l[id].b);
 }
 double ppdissqr(double x1,double y1,double x2,double y2)
 {
     return (x2-x1)*(x2-x1)+(y2-y1)*(y2-y1);
 }
 bool judge(double x)
 {
     for (int i=;i<=n;i++)
         if (l[i].dis-x<=-eps)
         {
             double A=l[i].a,B=l[i].b,C=l[i].c;
             if (B)
             {
                 double delta=((A/B)*(A/B)+)*x*x-((A*P.x+C)/B+P.y)*((A*P.x+C)/B+P.y),
                 x1=(-*(A/B*(C/B+P.y)-P.x)+sqrt(delta))/(*(+(A/B)*(A/B))),
                 x2=(-*(A/B*(C/B+P.y)-P.x)-sqrt(delta))/(*(+(A/B)*(A/B)));
                 double p=a[i].x,q=a[i+].x;
                 if (i==n) q=a[].x;
                 if (p>q) swap(p,q);
                 if ((x1>=p && x1<=q)
                 || (x2>=p && x2<=q))
                 return ;
             }
             else
             {
                 double y1=P.y+sqrt(x*x-(-C/A-P.x)*(-C/A-P.x)),
                        y2=P.y-sqrt(x*x-(-C/A-P.x)*(-C/A-P.x));
                 double p=a[i].y,q=a[i+].y;
                 if (i==n) q=a[].y;
                 if (p>q) swap(p,q);
                 if ((y1>=p && y1<=q)
                 || (y2>=p && y2<=q))
                 return ;
             }
         }
     return ;
 }
 int main()
 {
     scanf("%d%lf%lf",&n,&P.x,&P.y);
     for (int i=;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
     for (int i=;i<n;i++)
         do_line(i,a[i].x,a[i].y,a[i+].x,a[i+].y);
     do_line(n,a[n].x,a[n].y,a[].x,a[].y);
     double f1=0.0,r2,L=0.0,R;
     for (int i=;i<=n;i++)
         f1=max(f1,ppdissqr(a[i].x,a[i].y,P.x,P.y));
     R=sqrt(f1);
     for (int i=;i<=n;i++)
         R=min(R,sqrt(ppdissqr(a[i].x,a[i].y,P.x,P.y)));
     while (R-L>eps)
     {
         double mid=(L+R+eps)/;
         if (judge(mid)) L=mid;
         else R=mid-eps;
     }
     r2=(L+R)/;
     printf("%.10lf\n",pi*(f1-r2*r2));
     return ;
 }