1.1.2最小生成树（Kruskal和Prim算法）

部分内容摘自 勿在浮沙筑高台

http://blog.csdn.net/luoshixian099/article/details/51908175

关于图的几个概念定义：

• 连通图：在无向图中，若任意两个顶点v_i与v_j都有路径相通，则称该无向图为连通图。
• 强连通图：在有向图中，若任意两个顶点v_i与v_j都有路径相通，则称该有向图为强连通图。
• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
• 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
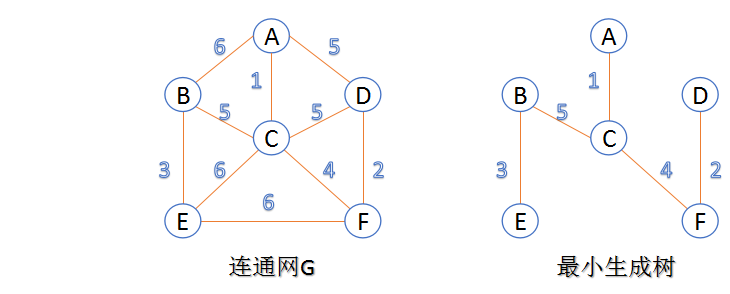
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

下面介绍两种求最小生成树算法

1.Kruskal算法

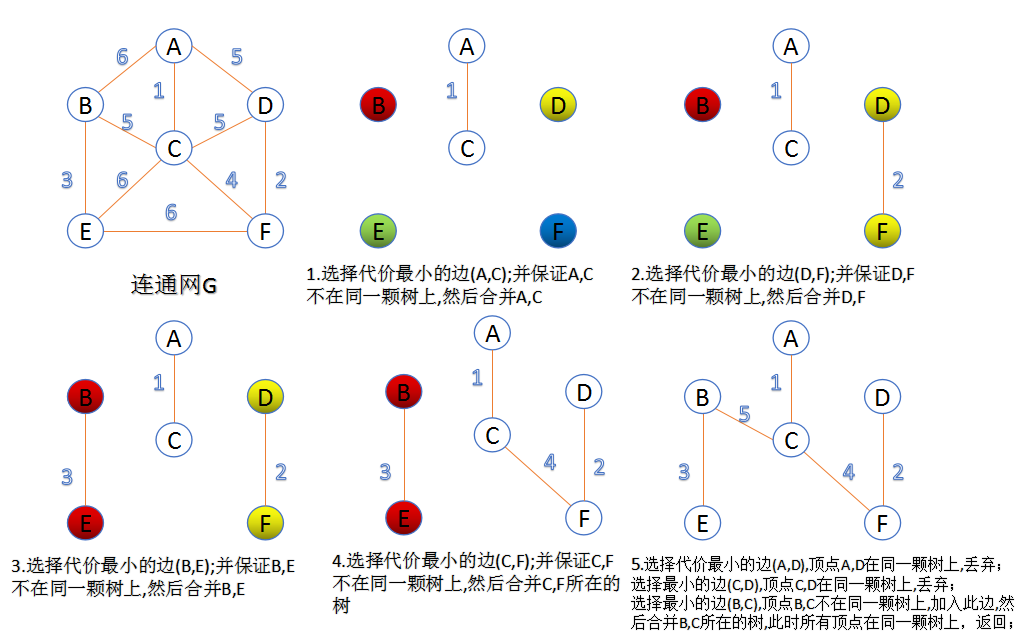
此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

1. 把图中的所有边按代价从小到大排序；

2. 把图中的n个顶点看成独立的n棵树组成的森林；

3. 按权值从小到大选择边，所选的边连接的两个顶点u_i,v_i,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。

4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

2.Prim算法

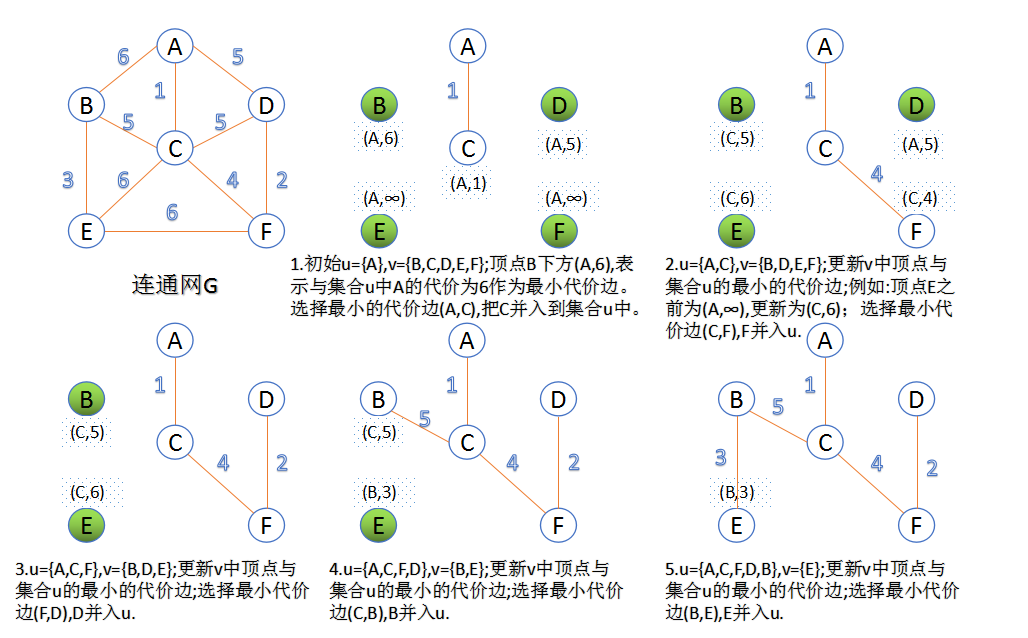
此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

图的所有顶点集合为VV；初始令集合 u=s,v=V−uu=s,v=V−u" role="presentation">u=s,v=V−uu=s,v=V−uu=s,v=V−uu=s,v=V−u;

在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u₀,v₀)，加入到最小生成树中，并把v₀并入到集合u中。

重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息，：

struct
{
  char vertexData   //表示u中顶点信息
  UINT lowestcost   //最小代价
}closedge[vexCounts]

3.最小生成树Kruskal算法+并查集实现

Veegin博客

HDU 1863 畅通工程（Kruskal+并查集）

4.最小生成树 Prim算法

POJ 1258 Agri-Net(Prim求最小生成树)