圆方树总结 [uoj30]Tourists

圆方树总结

所谓圆方树就是把一张图变成一棵树。

怎么变啊qaq

这里盗一张图



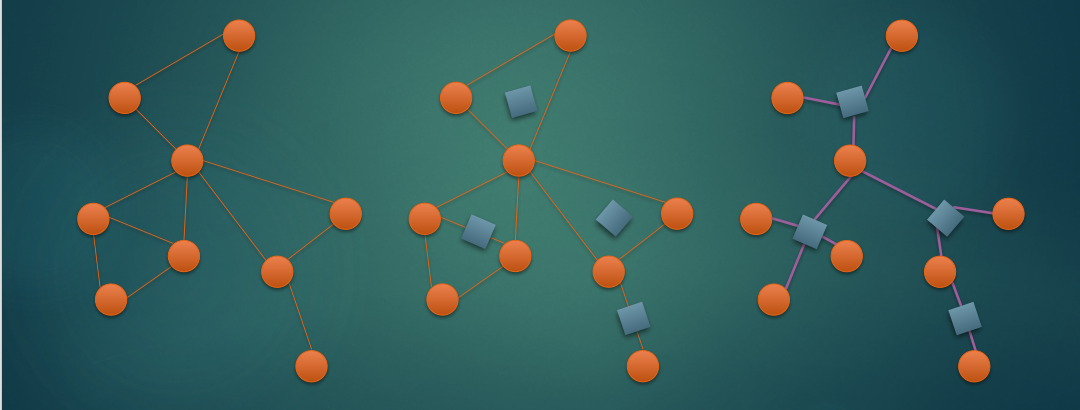
简单来说就是给每一个点双新建一个点，然后连向这个点双中的每一个点。特殊的，把两个点互相连通的也视作一个点双。

我们把原来就有的点称作圆点，因点双而新建的点称之为方点。

这样这棵圆方树就会有一个这样的性质：和每个圆点（方点）相连的点一定是方点（圆点）。

我们在每个圆点上维护这个点原本的信息，在方点上维护这个点双的信息，这样就能完成一些关于一般图的所有简单路径的询问了。

例如：我现在有一张一般图，每个点有一个点权，要求从\(u\)到\(v\)的所有简单路径中经过的最小点权是多少。

可以建出圆方树，在每个方点上维护这个点双中的最小点权，那么每次询问就是查询一个路径最小值了。

如果有修改怎么办呢？直接改完圆点后改和它相邻的方点？

显然这个复杂度是\(O(度数)\)的，很容易卡成\(O(n^2)\)

方法：每个方点维护的信息中不包括它的父亲圆点，这样修改圆点的时候就只需要修改它的父亲方点。查询的时候如果路径的\(lca\)是个方点，就还要再算上它的父亲圆点。

是不是很妙？

uoj30

就是上面讲的那个东西。

圆方树+可删除堆+树链剖分+线段树

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
int gi(){
	int x=0,w=1;char ch=getchar();
	while ((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
	if (ch=='-') w=0,ch=getchar();
	while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
	return w?x:-x;
}
const int N = 4e5+5;
int n,tot,m,q,val[N],dfn[N],low[N],tim,S[N];
int fa[N],dep[N],sz[N],son[N],top[N],mn[N<<2];
struct Set{
	priority_queue<int,vector<int>,greater<int> >Q1,Q2;
	void insert(int x){Q1.push(x);}
	void erase(int x){Q2.push(x);}
	int top(){
		while (!Q2.empty()&&Q1.top()==Q2.top()) Q1.pop(),Q2.pop();
		return Q1.top();
	}
}Q[N];
struct Graph{
	int to[N],nxt[N],head[N],cnt;
	void link(int u,int v){
		to[++cnt]=v;nxt[cnt]=head[u];head[u]=cnt;
		to[++cnt]=u;nxt[cnt]=head[v];head[v]=cnt;
	}
}G1,G2;
void Tarjan(int u){
	dfn[u]=low[u]=++tim;S[++S[0]]=u;
	for (int e=G1.head[u];e;e=G1.nxt[e]){
		int v=G1.to[e];
		if (!dfn[v]){
			Tarjan(v),low[u]=min(low[u],low[v]);
			if (low[v]>=dfn[u]){
				G2.link(++tot,u);int x=0;
				do{
					x=S[S[0]--];G2.link(tot,x);
				}while (x!=v);
			}
		}
		else low[u]=min(low[u],dfn[v]);
	}
}
void dfs1(int u,int f){
	fa[u]=f;dep[u]=dep[f]+1;sz[u]=1;
	if (u<=n&&f) Q[f].insert(val[u]);
	for (int e=G2.head[u];e;e=G2.nxt[e]){
		int v=G2.to[e];if (v==f) continue;
		dfs1(v,u);sz[u]+=sz[v];
		if (sz[v]>sz[son[u]]) son[u]=v;
	}
}
void dfs2(int u,int up){
	top[u]=up;dfn[u]=++tim;
	if (son[u]) dfs2(son[u],up);
	for (int e=G2.head[u];e;e=G2.nxt[e]){
		int v=G2.to[e];if (v==fa[u]||v==son[u]) continue;
		dfs2(v,v);
	}
}
void modify(int x,int l,int r,int p,int v){
	if (l==r) {mn[x]=v;return;}
	int mid=l+r>>1;
	if (p<=mid) modify(x<<1,l,mid,p,v);
	else modify(x<<1|1,mid+1,r,p,v);
	mn[x]=min(mn[x<<1],mn[x<<1|1]);
}
int query(int x,int l,int r,int ql,int qr){
	if (l>=ql&&r<=qr) return mn[x];
	int mid=l+r>>1;
	if (qr<=mid) return query(x<<1,l,mid,ql,qr);
	if (ql>mid) return query(x<<1|1,mid+1,r,ql,qr);
	return min(query(x<<1,l,mid,ql,qr),query(x<<1|1,mid+1,r,ql,qr));
}
int main(){
	tot=n=gi();m=gi();q=gi();
	for (int i=1;i<=n;++i) val[i]=gi();
	while (m--){
		int u=gi(),v=gi();
		G1.link(u,v);
	}
	for (int i=1;i<=n;++i) if (!dfn[i]) Tarjan(i);
	tim=0;dfs1(1,0),dfs2(1,1);
	for (int i=1;i<=n;++i) modify(1,1,tot,dfn[i],val[i]);
	for (int i=n+1;i<=tot;++i) modify(1,1,tot,dfn[i],Q[i].top());
	while (q--){
		char ch='%';while (ch!='A'&&ch!='C') ch=getchar();
		if (ch=='C'){
			int a=gi(),b=gi();
			if (fa[a]) Q[fa[a]].erase(val[a]);
			val[a]=b;modify(1,1,tot,dfn[a],val[a]);
			if (fa[a]) Q[fa[a]].insert(val[a]),modify(1,1,tot,dfn[fa[a]],Q[fa[a]].top());
		}
		else{
			int u=gi(),v=gi(),ans=2e9;
			while (top[u]^top[v]){
				if (dep[top[u]]<dep[top[v]]) swap(u,v);
				ans=min(ans,query(1,1,tot,dfn[top[u]],dfn[u]));
				u=fa[top[u]];
			}
			if (dep[u]>dep[v]) swap(u,v);
			ans=min(ans,query(1,1,tot,dfn[u],dfn[v]));
			if (u>n) ans=min(ans,val[fa[u]]);
			printf("%d\n",ans);
		}
	}
	return 0;
}

圆方树与仙人掌

留坑待补