Codeforces Round #177 (Div. 2) 题解

【前言】咦？如今怎么流行打CF了？于是当一帮大爷在执着的打div 1的时候，我偷偷的在刷div 2。至于怎么决定场次嘛。一般我报一个数字A，随便再拉一个人选一个数字B。然后開始做第A^B场。假设认为机密性不高，来点取模吧。

然后今天做的这场少有的AK了。（事实上模拟赛仅仅做完了4题。最后1题来不及打了）

等等。话说前面几题不用写题解了？算了，让我难得风光一下啦。

【A】

A. Polo the Penguin and Segments

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little penguin Polo adores integer segments, that is, pairs of integers [l; r] (l ≤ r).

He has a set that consists of n integer segments: [l1; r1], [l2; r2], ..., [ln; rn].
We know that no two segments of this set intersect. In one move Polo can either widen any segment of the set 1 unit to the left or 1 unit to the right, that is transform [l; r] to
either segment[l - 1; r], or to segment [l; r + 1].

The value of a set of segments that consists of n segments [l1; r1], [l2; r2], ..., [ln; rn] is
the number of integers x, such that there is integer j,
for which the following inequality holds, lj ≤ x ≤ rj.

Find the minimum number of moves needed to make the value of the set of Polo's segments divisible by k.

Input

The first line contains two integers n and k (1 ≤ n, k ≤ 105).
Each of the following n lines contain a segment as a pair of integers li andri ( - 105 ≤ li ≤ ri ≤ 105),
separated by a space.

It is guaranteed that no two segments intersect. In other words, for any two integers i, j (1 ≤ i < j ≤ n) the
following inequality holds,min(ri, rj) < max(li, lj).

Output

In a single line print a single integer — the answer to the problem.

Sample test(s)

input

2 3
1 2
3 4

output

2

input

3 7
1 2
3 3
4 7

output

0

这道题究竟有什么意思呢？反正题目是模模糊糊的看懂的。

好像是给定N个段和数K，你能够把某一段的L减一，把某一段的R加一，都算一次操作。终于要使得总长度%K=0。求最少操作次数。

直接贴代码算了。

#include<cstdio>
using namespace std;
int n,k,i,ans,x,y;
int main()
{
  scanf("%d%d",&n,&k);
  for (i=1;i<=n;i++)
    scanf("%d%d",&x,&y),ans+=y-x+1;
  if (ans%k==0) puts("0");
  else printf("%d",k-ans%k);
  return 0;
}

【B】

B. Polo the Penguin and Matrix

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little penguin Polo has an n × m matrix, consisting of integers. Let's index the matrix rows from 1 to n from
top to bottom and let's index the columns from 1 to m from left to right. Let's represent the matrix element on the intersection of row i and
column j as aij.

In one move the penguin can add or subtract number d from some matrix element. Find the minimum number of moves needed to make all matrix elements equal.
If the described plan is impossible to carry out, say so.

Input

The first line contains three integers n, m and d (1 ≤ n, m ≤ 100, 1 ≤ d ≤ 104) —
the matrix sizes and the d parameter. Next n lines
contain the matrix: the j-th integer in the i-th
row is the matrix element aij (1 ≤ aij ≤ 104).

Output

In a single line print a single integer — the minimum number of moves the penguin needs to make all matrix elements equal. If that is impossible, print "-1" (without
the quotes).

Sample test(s)

input

2 2 2
2 4
6 8

output

4

input

1 2 7
6 7

output

-1

题意是给出N*M个带权方格，每次操作仅仅能对每一个格子+或-d。

求把全部方块变成同样的权值最小操作次数，无解输出-1。判是否有解解非常easy，仅仅要权值A%d是否是定值，或者ΔA%d是否=0。

假设有解的话一定是改成中位数。

#include<cstdio>
#include<algorithm>
using namespace std;
int a[100005],num,n,m,d,i,j,tot,ans;
int main()
{
  scanf("%d%d%d",&n,&m,&d);
  scanf("%d",&a[tot=1]);num=a[1]%d;
  for (i=1;i<=n;i++)
    for (j=1;j<=m;j++)
    {
      if (i==1&&j==1) continue;
      scanf("%d",&a[++tot]);
      if (a[tot]%d!=num) {puts("-1");return 0;}
    }
  sort(a+1,a+tot+1);
  for (i=1;i<=tot;i++)
    ans+=abs(a[i]-a[(tot+1)>>1])/d;
  printf("%d",ans);
  return 0;
}

【C】

C. Polo the Penguin and Strings

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little penguin Polo adores strings. But most of all he adores strings of length n.

One day he wanted to find a string that meets the following conditions:

1. The string consists of n lowercase English letters (that is, the string's length equals n),
   exactly k of these letters are distinct.
2. No two neighbouring letters of a string coincide; that is, if we represent a string as s = s1s2... sn,
   then the following inequality holds,si ≠ si + 1(1 ≤ i < n).
3. Among all strings that meet points 1 and 2, the required string is lexicographically smallest.

Help him find such string or state that such string doesn't exist.

String x = x1x2... xp is lexicographically
less than string y = y1y2... yq,
if either p < q and x1 = y1, x2 = y2, ...
, xp = yp,
or there is such number r (r < p, r < q),
that x1 = y1, x2 = y2, ...
, xr = yr and xr + 1 < yr + 1.
The characters of the strings are compared by their ASCII codes.

Input

A single line contains two positive integers n and k (1 ≤ n ≤ 106, 1 ≤ k ≤ 26) —
the string's length and the number of distinct letters.

Output

In a single line print the required string. If there isn't such string, print "-1" (without the quotes).

Sample test(s)

input

7 4

output

ababacd

input

4 7

output

-1

构造题。

构造一个字典序最小的小写字符串。使得相邻两个字母不同。并且恰好仅仅按顺序出现了K个字母。大概的想法就是前面一直a和b交替，后来K-2位一直沿着c，d。e放下去。

注意这道题是有cha点的。

假设K=1，显然是无解，由于相邻两个不能同样。可是当N=1时还是正确的：'a'！

#include<cstdio>
#define PR ({puts("-1");return 0;})
using namespace std;
int n,i,m;
int main()
{
  scanf("%d%d",&n,&m);
  if (m==1&&n==1) {putchar('a');return 0;}
  if (m>n||m==1) PR;
  for (i=1;i<=n-(m-2);i++)
    if (i&1) putchar('a');else putchar('b');
  for (i=1;i<=m-2;i++) putchar((char)(i+98));
  return 0;
}

【D】

D. Polo the Penguin and Houses

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little penguin Polo loves his home village. The village has n houses, indexed by integers from 1 to n.
Each house has a plaque containing an integer, the i-th house has a plaque containing integer pi (1 ≤ pi ≤ n).

Little penguin Polo loves walking around this village. The walk looks like that. First he stands by a house number x. Then he goes to the house whose number
is written on the plaque of house x (that is, to house px),
then he goes to the house whose number is written on the plaque of house px (that
is, to house ppx),
and so on.

We know that:

1. When the penguin starts walking from any house indexed from 1 to k, inclusive, he can walk to house number 1.
2. When the penguin starts walking from any house indexed from k + 1 to n,
   inclusive, he definitely cannot walk to house number 1.
3. When the penguin starts walking from house number 1, he can get back to house number 1 after some non-zero number of walks from a house to a house.

You need to find the number of ways you may write the numbers on the houses' plaques so as to fulfill the three above described conditions. Print the remainder after dividing this number by 1000000007 (109 + 7).

Input

The single line contains two space-separated integers n and k (1 ≤ n ≤ 1000, 1 ≤ k ≤ min(8, n))
— the number of the houses and the number k from the statement.

Output

In a single line print a single integer — the answer to the problem modulo 1000000007 (109 + 7).

Sample test(s)

input

5 2

output

54

input

7 4

output

1728

開始还以为是DP。然后题意看了半天。大意是有N个房子，让你给每一个房子加一个“索引”P，当你到了X后，你下一次去Px。

再给定一个数K。对索引有下列三个要求：

①从1号点走出去后必须能回到1号点。

②从前K号点走出去后必须能回到1号点。（为什么认为上面一个是多余的？）

③从K+1~N号点走出去后必须不能回到1号点。

求全部索引的方案取模10^9+7的值。

对于K+1~N号点。显然和1~K是隔绝的。因此方案数是简单的计算(N-K)^(N-K)。

对于1号点。显然它能够填K种索引。

对于2~K号点，開始我束手无策。

后来发现K<=8!那么仅仅要简单的dfs一下，再验证一下就可以。

最后用乘法原理把三者乘起来。

#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
const LL P=1000000007ll;
int a[10],f[10],i;
LL num,ans,n,k;
int work(int k,int flag)
{
  f[k]=flag;if (k==1) return 1;
  if (f[a[k]]!=flag) return work(a[k],flag);
  return 0;
}
inline void check()
{
  int ok=1;memset(f,0,sizeof(f));
  for (int i=2;i<=k&&ok;i++)
    ok&=work(i,i);
  if (ok) num++;
}
void dfs(int now)
{
  if (now==k+1) {check();return;}
  for (int i=1;i<=k;i++)
    a[now]=i,dfs(now+1);
}
int main()
{
  scanf("%I64d%I64d",&n,&k);ans=k;
  for (i=1;i<=n-k;i++)
    (ans*=(n-k))%=P;
  dfs(2);
  if (num) (ans*=num)%=P;
  printf("%I64d",ans);
  return 0;
}

【E】

E. Polo the Penguin and XOR operation

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little penguin Polo likes permutations. But most of all he likes permutations of integers from 0 to n,
inclusive.

For permutation p = p0, p1, ..., pn,
Polo has defined its beauty — number .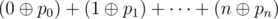

Expression 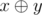 means
applying the operation of bitwise excluding "OR" to numbers x and y.
This operation exists in all modern programming languages, for example, in language C++ and Java it is represented as "^"
and in Pascal — as "xor".

Help him find among all permutations of integers from 0 to n the
permutation with the maximum beauty.

Input

The single line contains a positive integer n (1 ≤ n ≤ 106).

Output

In the first line print integer m the maximum possible beauty. In the second line print any permutation of integers from 0 to n with
the beauty equal to m.

If there are several suitable permutations, you are allowed to print any of them.

Sample test(s)

input

4

output

20
0 2 1 4 3

题意非常清楚。求0~N的排列Ai，使得max{Σi^A[i]}。

開始以为是从大到小枚举i，在字母树中贪心地找与它尽量能匹配的。后来打表后发现是一一相应的，不用这么麻烦。假设i没有被匹配过，我们能够构造出k<i，且k和i匹配的值=k+i。然后扫一遍就可以。

这里是打表程序：

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,sum,t,now,ans,i,wri[10005][105],a[105];
int main()
{
  freopen("1.txt","w",stdout);
  for (n=3;n<=9;n++)
  {
  sum=1;int F=0;
  for (i=0;i<=n;i++)
    a[i]=i,sum*=(n+1-i);
  ans=0;
  for (t=1;t<=sum;t++)
  {
    now=0;
    for (i=0;i<=n;i++)
      now+=(i^a[i]);
    if (now>ans)
      ans=now,F=1,memcpy(wri[1],a,sizeof(a));
    else if (now==ans) memcpy(wri[++F],a,sizeof(a));
    next_permutation(a,a+n+1);
  }
  printf("%d %d\n",n,ans);
  for (int j=1;j<=F;j++)
  {
    for (i=0;i<=n;i++) printf("%d ",wri[j][i]);
    puts("");
  }
  puts("");
  }
  return 0;
}

这里是AC程序：

#include<cstdio>
#include<cmath>
using namespace std;
int a[25],f[1000005],x,k,i,n;long long ans=0;
int main()
{
  scanf("%d",&n);
  for (i=n;i;i--)
    if (!f[i])
    {
      k=(int)(log2(i))+1;x=(1<<k)-1-i;
      f[x]=1;a[i]=x;a[x]=i;ans+=(long long)((1<<k)-1)<<1;
    }
  printf("%I64d\n",ans);
  for (i=0;i<=n;i++) printf("%d ",a[i]);
}