Java中PriorityQueue详解

Java中PriorityQueue通过二叉小顶堆实现，可以用一棵完全二叉树表示。本文从Queue接口函数出发，结合生动的图解，深入浅出地分析PriorityQueue每个操作的具体过程和时间复杂度，将让读者建立对PriorityQueue建立清晰而深入的认识。

总体介绍

前面以Java ArrayDeque为例讲解了Stack和Queue，其实还有一种特殊的队列叫做PriorityQueue，即优先队列。优先队列的作用是能保证每次取出的元素都是队列中权值最小的（Java的优先队列每次取最小元素，C++的优先队列每次取最大元素）。这里牵涉到了大小关系，元素大小的评判可以通过元素本身的自然顺序（natural ordering），也可以通过构造时传入的比较器（Comparator，类似于C++的仿函数）。

Java中PriorityQueue实现了Queue接口，不允许放入null元素；其通过堆实现，具体说是通过完全二叉树（complete binary tree）实现的小顶堆（任意一个非叶子节点的权值，都不大于其左右子节点的权值），也就意味着可以通过数组来作为PriorityQueue的底层实现。

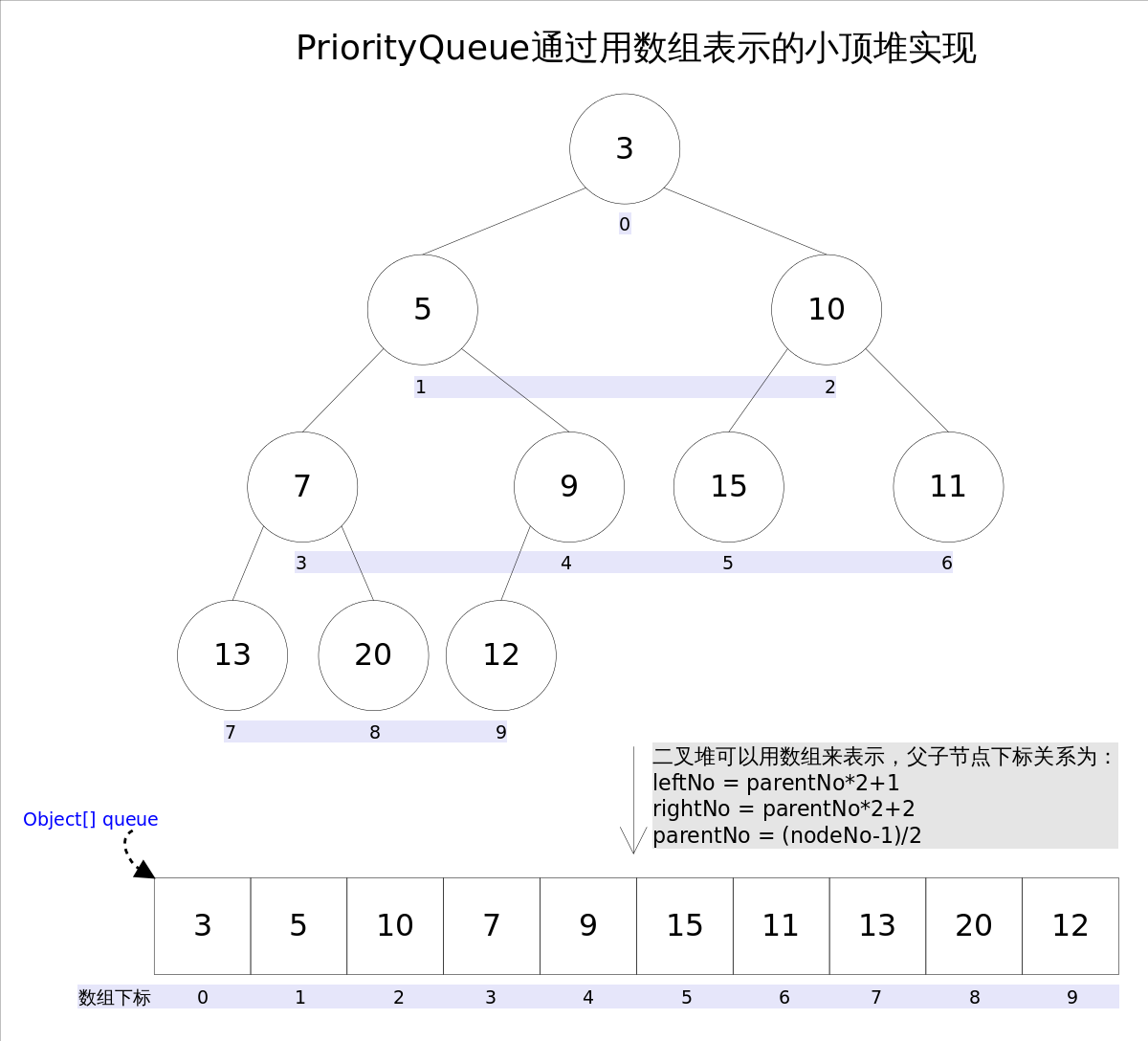
上图中我们给每个元素按照层序遍历的方式进行了编号，如果你足够细心，会发现父节点和子节点的编号是有联系的，更确切的说父子节点的编号之间有如下关系：

leftNo = parentNo*2+1

rightNo = parentNo*2+2

parentNo = (nodeNo-1)/2

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。

PriorityQueue的peek()和element操作是常数时间，add(), offer(), 无参数的remove()以及poll()方法的时间复杂度都是log(N)。

方法剖析

add()和offer()

add(E e)和offer(E e)的语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则则会返回false。对于PriorityQueue这两个方法其实没什么差别。

新加入的元素可能会破坏小顶堆的性质，因此需要进行必要的调整。

//offer(E e)
public boolean offer(E e) {
    if (e == null)//不允许放入null元素
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1);//自动扩容
    size = i + 1;
    if (i == 0)//队列原来为空，这是插入的第一个元素
        queue[0] = e;
    else
        siftUp(i, e);//调整
    return true;
}

上述代码中，扩容函数grow()类似于ArrayList里的grow()函数，就是再申请一个更大的数组，并将原数组的元素复制过去，这里不再赘述。需要注意的是siftUp(int k, E x)方法，该方法用于插入元素x并维持堆的特性。

//siftUp()
private void siftUp(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;//parentNo = (nodeNo-1)/2
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)//调用比较器的比较方法
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

新加入的元素x可能会破坏小顶堆的性质，因此需要进行调整。调整的过程为：从k指定的位置开始，将x逐层与当前点的parent进行比较并交换，直到满足x >= queue[parent]为止。注意这里的比较可以是元素的自然顺序，也可以是依靠比较器的顺序。

element()和peek()

element()和peek()的语义完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素，二者唯一的区别是当方法失败时前者抛出异常，后者返回null。根据小顶堆的性质，堆顶那个元素就是全局最小的那个；由于堆用数组表示，根据下标关系，0下标处的那个元素既是堆顶元素。所以直接返回数组0下标处的那个元素即可。

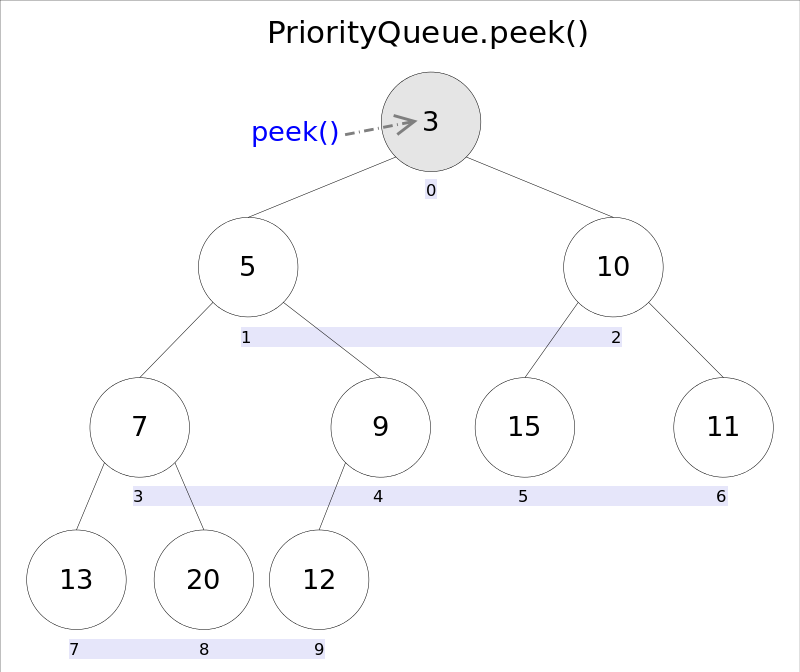
代码也就非常简洁：

//peek()
public E peek() {
    if (size == 0)
        return null;
    return (E) queue[0];//0下标处的那个元素就是最小的那个
}

remove()和poll()

remove()和poll()方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。

代码如下：

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];//0下标处的那个元素就是最小的那个
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x);//调整
    return result;
}

上述代码首先记录0下标处的元素，并用最后一个元素替换0下标位置的元素，之后调用siftDown()方法对堆进行调整，最后返回原来0下标处的那个元素（也就是最小的那个元素）。重点是siftDown(int k, E x)方法，该方法的作用是从k指定的位置开始，将x逐层向下与当前点的左右孩子中较小的那个交换，直到x小于或等于左右孩子中的任何一个为止。

//siftDown()
private void siftDown(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        //首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标
        int child = (k << 1) + 1;//leftNo = parentNo*2+1
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c;//然后用c取代原来的值
        k = child;
    }
    queue[k] = x;
}

remove(Object o)

remove(Object o)方法用于删除队列中跟o相等的某一个元素（如果有多个相等，只删除一个），该方法不是Queue接口内的方法，而是Collection接口的方法。由于删除操作会改变队列结构，所以要进行调整；又由于删除元素的位置可能是任意的，所以调整过程比其它函数稍加繁琐。具体来说，remove(Object o)可以分为2种情况：1. 删除的是最后一个元素。直接删除即可，不需要调整。2. 删除的不是最后一个元素，从删除点开始以最后一个元素为参照调用一次siftDown()即可。此处不再赘述。

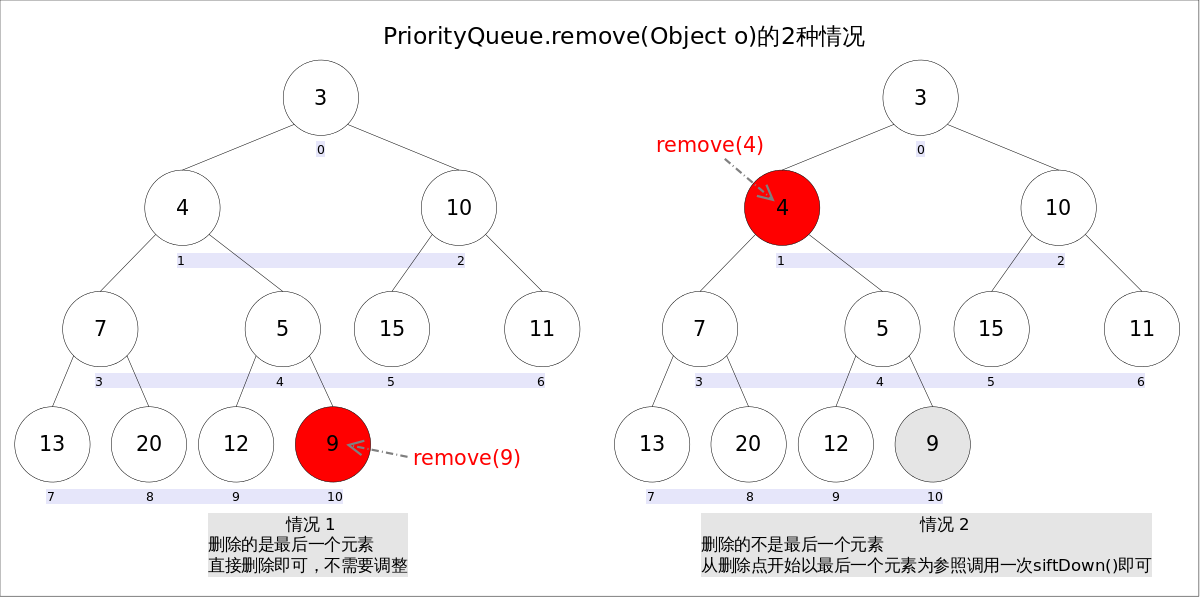
具体代码如下：

//remove(Object o)
public boolean remove(Object o) {
    //通过遍历数组的方式找到第一个满足o.equals(queue[i])元素的下标
    int i = indexOf(o);
    if (i == -1)
        return false;
    int s = --size;
    if (s == i) //情况1
        queue[i] = null;
    else {
        E moved = (E) queue[s];
        queue[s] = null;
        siftDown(i, moved);//情况2
        ......
    }
    return true;
}