cf486B OR in Matrix

B. OR in Matrix

time limit per test 1 second

memory limit per test 256 megabytes

input standard input

output standard output

Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:

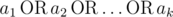 where 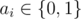 is equal to 1 if some ai = 1, otherwise it is equal to 0.

Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as Aij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:

.

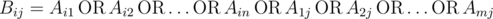(Bij is OR of all elements in row i and column j of matrix A)

Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.

Input

The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.

The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).

Output

In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print mrows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.

Sample test(s)

input

2 2
1 0
0 0

output

NO

input

2 3
1 1 1
1 1 1

output

YES
1 1 1
1 1 1

input

2 3
0 1 0
1 1 1

output

YES
0 0 0
0 1 0

题意是一个矩阵B的b[i][j]是所有A矩阵的a[i][k]和a[k][j]或起来的值，给一个B矩阵，问是否存在这样的A矩阵，并输出方案
因为是或……所以在B中出现的0必须在A中一横一竖都为0
所以先把B中0的情况搞完，然后判一下现在的B矩阵中1的位置对应的A的一行一列是否存在至少一个1
15分钟……有些慢了，你看卓神6分钟A掉

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<ctime>
#define LL long long
#define inf 0x7ffffff
#define pa pair<int,int>
#define pi 3.1415926535897932384626433832795028841971
using namespace std;
int mat[110][110];
int a[110][110];
int n,m;
inline LL read()
{
    LL x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
void ex()
{
	printf("NO");
	exit(0);
}
int main()
{
	n=read();m=read();
	for (int i=1;i<=n;i++)
	for (int j=1;j<=m;j++)
	mat[i][j]=1;
	for (int i=1;i<=n;i++)
	for (int j=1;j<=m;j++)
	a[i][j]=read();
	for (int i=1;i<=n;i++)
	for (int j=1;j<=m;j++)
	{
		int x=a[i][j];
		if (!x)
		{
		  for (int k=1;k<=n;k++)
		    mat[k][j]=0;
		  for (int k=1;k<=m;k++)
			mat[i][k]=0;
		}
	}
	for (int i=1;i<=n;i++)
	for (int j=1;j<=m;j++)
	  if(a[i][j])
	  {
	  	  bool mrk=0;
		  for (int k=1;k<=n;k++)if (mat[k][j])mrk=1;
		  for (int k=1;k<=m;k++)if (mat[i][k])mrk=1;
		  if (!mrk)ex();
	  }
	printf("YES\n");
	for (int i=1;i<=n;i++)
	{
		for (int j=1;j<=m;j++)
		  printf("%d ",mat[i][j]);
		printf("\n");
	}
}