带权并查集【bzoj3362】: [Usaco2004 Feb]Navigation Nightmare 导航噩梦

【bzoj】3362: [Usaco2004 Feb]Navigation Nightmare 导航噩梦

​ 农夫约翰有N(2≤N≤40000)个农场，标号1到N,M(2≤M≤40000)条的不同的垂直或水

平的道路连结着农场，道路的长度不超过1000.这些农场的分布就像下面的地图一样，

图中农场用F1..F7表示, 每个农场最多能在东西南北四个方向连结4个不同的农场．此外，农场只处在道路的两端．道路不会交叉且每对农场间有且仅有一条路径．邻居鲍伯要约翰来导航，但约翰丢了农场的地图，他只得从电脑的备份中修复了．每一条道路的信息如下：

从农场23往南经距离10到达农场17

从农场1往东经距离7到达农场17

​ 当约翰重新获得这些数据时，他有时被的鲍伯的问题打断：“农场1到农场23的曼哈顿距离是多少？”所谓在(XI，Yi)和(X2，y2)之间的“曼哈顿距离”，就是lxl - X21+lyl - y21．如果已经有足够的信息，约翰就会回答这样的问题（在上例中答案是17），否则他会诚恳地抱歉并回答-1.

Input

​ 第1行：两个分开的整数N和M.

​ 第2到M+1行：每行包括4个分开的内容，F1，F2，三，D分别描述两个农场的编号，道路的长度，F1到F2的方向N，E，S，w．

​ 第M+2行：一个整数，K(1≤K≤10000)，表示问题个数．

​ 第M+3到M+K+2行：每行表示一个问题，由3部分组成：Fi，F2，，．其中Fi和F2表示两个被问及的农场．而/(1≤J≤M)表示问题提出的时刻．J为1时，表示得知信息1但未得知信息2时．

Output

​ 第1到K行：每行一个整数，回答问题．表示两个农场间的曼哈顿距离．不得而知则输出-1.

两点之间只有一条路径，所以这是一颗树。又因为要判断两点是否连通，可以想到用并查集维护。

又因为要维护两点之间的曼哈顿距离，所以用带权并查集维护每个点到其祖先的x距离和y距离。

带权并查集小白表示这道题让我很难受。

首先在路径压缩的时候，代码很容易写出来：

int find(int x){
	if(f[x]==x)return x;
    itn t=f[x];
    f[x]=find(f[x]);
    dx[x]+=dx[t];
    dy[x]+=dy[t];
    return f[x];
}

之后我们把操作排序离线。

那么对于合并的操作，我认为才是最大的难点。

首先给出代码：

while(now<=q[i].p){
	int ta=find(q[i].x);int tb=find(q[i].y);
    if(ta!=tb){
		f[ta]=tb;
         dx[ta]=dx[b[now]]+cx[now]-dx[a[now]];
         dy[ta]=dy[b[now]]+cy[now]-dy[a[now]];
    }
    now++;
}

重点是对于dx和dy的更新。

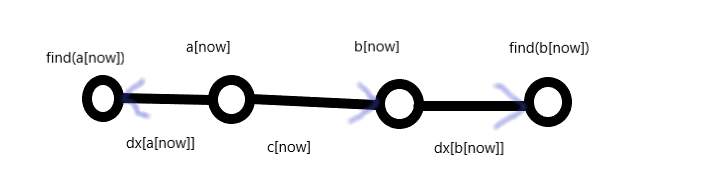
那画个图其实就好理解了。

注意边是有方向的。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int wx=40017;
int f[wx],dx[wx],dy[wx],a[wx],b[wx],cx[wx],cy[wx],ans[wx];
int n,m,t;
char opt[5];
inline int read(){
	int sum=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0';ch=getchar();}
	return sum*f;
}
int find(int x){
	if(x==f[x])return x;
	int t=f[x];
	f[x]=find(f[x]);
	dx[x]+=dx[t];
	dy[x]+=dy[t];
	return f[x];
}
struct node{
	int x,y,p,id;
	friend bool operator < (const node& a,const node& b)
	{
		return a.p<b.p;
	}
}q[wx];
int main(){
	n=read();read();
	for(int i=1;i<=n;i++)f[i]=i;
	for(int i=1;i<n;i++){
		a[i]=read();b[i]=read();t=read();scanf("%s",opt+1);
		if(opt[1]=='E')cx[i]=t;
		if(opt[1]=='W')cx[i]=-t;
		if(opt[1]=='N')cy[i]=t;
		if(opt[1]=='S')cy[i]-=t;
	}
	m=read();
	for(int i=1;i<=m;i++){
		q[i].x=read();q[i].y=read();q[i].p=read();q[i].id=i;
	}
	sort(q+1,q+1+m);
	int now=1;
	for(int i=1;i<=m;i++){
		while(now<=q[i].p){
			int ta=find(a[now]);
			int tb=find(b[now]);
			if(ta!=tb){
				f[ta]=tb;
				dx[ta]=dx[b[now]]+cx[now]-dx[a[now]];
				dy[ta]=dy[b[now]]+cy[now]-dy[a[now]];
			}
			now++;
		}
		int ta=find(q[i].x),tb=find(q[i].y);
		ans[q[i].id]=(ta==tb?abs(dx[q[i].x]-dx[q[i].y])+abs(dy[q[i].x]-dy[q[i].y]):-1);
//		now++;
	}
	for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
	return 0;
}