算法学习笔记(39): 2-SAT

SAT 问题，也就是可满足性问题 Boolean Satisfiability Problem，是第一个被证明的 NPC 问题。

但是特殊的 2-SAT 我们可以通过图论的知识在线性复杂度内求解，构造出一组解。

基本的模型在 P4782 【模板】2-SAT 中有体现。

经典的标志是：AB 至少选一个，AB 要么都选，要么都不选。

简单的我们就不说了，像 P5782 [POI2001]和平委员会，P6378 [PA2010] Riddle，P4171 [JSOI2010] 满汉全席，P5782 [POI2001] 和平委员会，都是很好的板子。

根据 伍昱 -《由对称性解 2-sat 问题》，我们可以得出：如果要输出 2-SAT 问题的一个可行解，只需要在 tarjan 缩点后所得的 DAG 上自底向上地进行选择和删除。

也就是优先选择缩点后所在连通块编号小的即可。

然而怎么会有这么板板的问题……

---

给定一个 0/1权有向图，给每个点赋予 ABCD 中的一个字母使得每条有向边都满足：\(w = 1 \iff (t_x, t_y) \in \{(A, D), (A, B), (B, D), (B, A), (C, D), (C, A), (C, B)\}\)

这一眼看不出来是 2-SAT，将关系画出来，大概是：

于是可以分为两组，\(a, b\) 进行 2-SAT。

---

给定 \(n\) 对 \(m\) 维空间中的点对，求平行于坐标轴且能够覆盖每个点对中至少一个点的 \(m\) 维正方体的边长的最小值，点在正方体的边界上视为覆盖。

二分答案，好抽象，利用 2-SAT 判断。

假如当前选了某个点，那么每一维距离它 \(\gt x\) 的都不可以选，考虑排序之后，这一定是一段前缀和一段后缀，于是可以前后缀优化建图。

然而还有二选一的限制，\(\neg a \to b\) 即可。

于是总复杂度为 \(O(nk \log n)\)。

---

草莓城是一个个四个角坐标分别为 \(H \times W\) 的矩形，其中有

个草莓，草莓所在的点都是整点。现在要给每个草莓建一个大棚，满足大棚都处在城市内，且互不相交（指被多个大棚覆盖的区域面积为零）。要求每个大棚的形状为等腰直角三角形，对应草莓处于斜边的中点，且斜边与一条坐标轴平行、所有三角形的斜边长度相等。

请你设计一个方案使得斜边的长度最大。

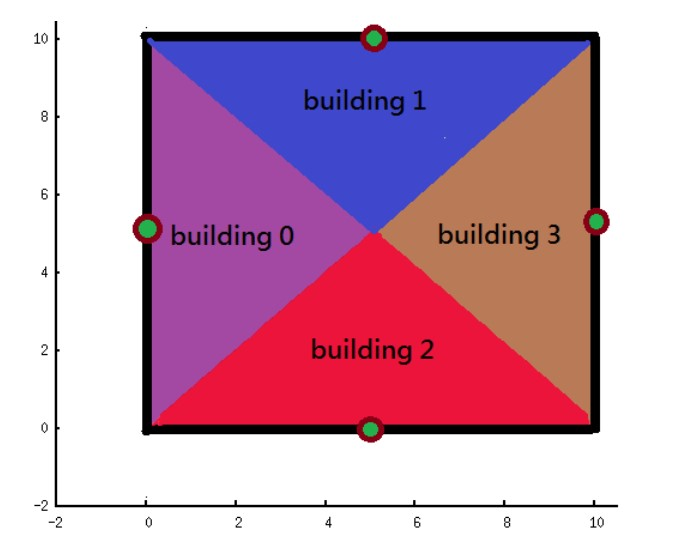是某种合法的方案。

还是二分 + 覆盖，这和上一题很类似。

但是每一个点有 \(4\) 个状态，于是成功的变成了 4-SAT NPC 问题，成功不可做。

然而可以注意到，将 \(4\) 中状态取交覆盖，发现我们只需要关注对角的二选一即可。

于是变成 \(AD\) 和 \(BC\) 两套 2-SAT 即可。

还有，我们可以 \(O(n^2)\) 建图，那么这道题就十分 naive 了。