力扣258(java)-各位相加（简单）

题目：

给定一个非负整数 num，反复将各个位上的数字相加，直到结果为一位数。返回这个结果。

示例 1:

输入: num = 38
输出: 2
解释: 各位相加的过程为：
38 --> 3 + 8 --> 11
11 --> 1 + 1 --> 2
由于 2 是一位数，所以返回 2。
示例 1:

输入: num = 0
输出: 0

提示：

0 <= num <= 231 - 1

进阶：你可以不使用循环或者递归，在 O(1) 时间复杂度内解决这个问题吗？

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/add-digits
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

一、模拟

模拟各位相加的过程，如果当前整数num > 9,分离出当前整数的每一位，进行相加，结束本轮相加后，将该轮的和赋值给num，然后进行新一轮的判断相加，直到和小于等于9退出循环，最后返回当前和即为答案。

代码：

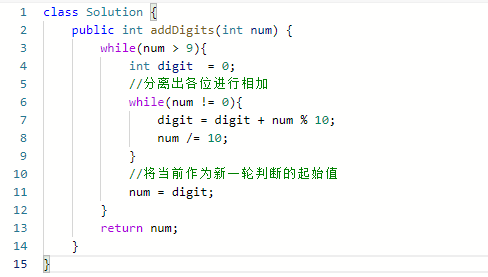
二、数学思维

题解思维来源@windliang

树根：

举例求1-30的树根：

结果为一位数，就是1-9循环出现，所以需要用到取余运算

观察树根变化规律，可以得出三种规律：

1.如果n为0，则树根为0；

2.如果n不是9的倍数，树根就为 n % 9;

3.如果n是9的倍数，树根就为9。

综合下来应该是这样的逻辑：

1 int addDigits(int num)
2 {
3     if(num > 0 &&  num % 9 == 0)
4     {
5         return 9;
6     }
7     return num % 9;
8 }

将上面的情况进行综合，将给定的数字n减 1，相当于原数整体向左偏移了 1，然后再将得到的数字对 9 取余，最后将得到的结果加 1 即可。所以如果原数是 n，树根就可以表示成 (n-1) mod 9 + 1

代码：

1 class Solution {
2     public int addDigits(int num) {
3         return (num - 1) % 9 + 1;
4     }
5 }