tensorflow：实战Google深度学习框架第四章02神经网络优化（学习率，避免过拟合，滑动平均模型）

1、学习率的设置既不能太小，又不能太大，解决方法：使用指数衰减法

例如：

假设我们要最小化函数 y=x2y=x2, 选择初始点 x0=5x0=5

 1. 学习率为1的时候，x在5和-5之间震荡。

import tensorflow as tf
TRAINING_STEPS = 10
LEARNING_RATE = 1
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)

train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        x_value = sess.run(x)
        print "After %s iteration(s): x%s is %f."% (i+1, i+1, x_value) 

After 1 iteration(s): x1 is -5.000000.
After 2 iteration(s): x2 is 5.000000.
After 3 iteration(s): x3 is -5.000000.
After 4 iteration(s): x4 is 5.000000.
After 5 iteration(s): x5 is -5.000000.
After 6 iteration(s): x6 is 5.000000.
After 7 iteration(s): x7 is -5.000000.
After 8 iteration(s): x8 is 5.000000.
After 9 iteration(s): x9 is -5.000000.
After 10 iteration(s): x10 is 5.000000.

2. 学习率为0.001的时候，下降速度过慢，在901轮时才收敛到0.823355

TRAINING_STEPS = 1000
LEARNING_RATE = 0.001
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)

train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        if i % 100 == 0:
            x_value = sess.run(x)
            print "After %s iteration(s): x%s is %f."% (i+1, i+1, x_value)

After 1 iteration(s): x1 is 4.990000.
After 101 iteration(s): x101 is 4.084646.
After 201 iteration(s): x201 is 3.343555.
After 301 iteration(s): x301 is 2.736923.
After 401 iteration(s): x401 is 2.240355.
After 501 iteration(s): x501 is 1.833880.
After 601 iteration(s): x601 is 1.501153.
After 701 iteration(s): x701 is 1.228794.
After 801 iteration(s): x801 is 1.005850.
After 901 iteration(s): x901 is 0.823355.

3. 使用指数衰减的学习率，在迭代初期得到较高的下降速度，可以在较小的训练轮数下取得不错的收敛程度

TRAINING_STEPS = 100
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True)

x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        if i % 10 == 0:
            LEARNING_RATE_value = sess.run(LEARNING_RATE)
            x_value = sess.run(x)
            print "After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value)

After 1 iteration(s): x1 is 4.000000, learning rate is 0.096000.
After 11 iteration(s): x11 is 0.690561, learning rate is 0.063824.
After 21 iteration(s): x21 is 0.222583, learning rate is 0.042432.
After 31 iteration(s): x31 is 0.106405, learning rate is 0.028210.
After 41 iteration(s): x41 is 0.065548, learning rate is 0.018755.
After 51 iteration(s): x51 is 0.047625, learning rate is 0.012469.
After 61 iteration(s): x61 is 0.038558, learning rate is 0.008290.
After 71 iteration(s): x71 is 0.033523, learning rate is 0.005511.
After 81 iteration(s): x81 is 0.030553, learning rate is 0.003664.
After 91 iteration(s): x91 is 0.028727, learning rate is 0.002436.

2、过拟合

要避免过拟合，解决办法：正则化

1. 生成模拟数据集。

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

data = []
label = []
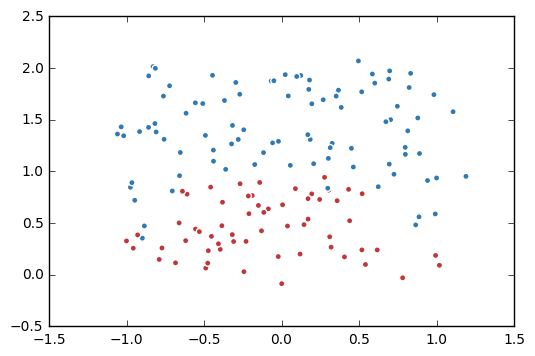
np.random.seed(0)

# 以原点为圆心，半径为1的圆把散点划分成红蓝两部分，并加入随机噪音。
for i in range(150):
    x1 = np.random.uniform(-1,1)
    x2 = np.random.uniform(0,2)
    if x1**2 + x2**2 <= 1:
        data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)])
        label.append(0)
    else:
        data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)])
        label.append(1)

data = np.hstack(data).reshape(-1,2)
label = np.hstack(label).reshape(-1, 1)
plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.show()

2. 定义一个获取权重，并自动加入正则项到损失的函数

def get_weight(shape, lambda1):
    var = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var))
    return var

3. 定义神经网络。

x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
sample_size = len(data)

# 每层节点的个数
layer_dimension = [2,10,5,3,1]

n_layers = len(layer_dimension)

cur_layer = x
in_dimension = layer_dimension[0]

# 循环生成网络结构
for i in range(1, n_layers):
    out_dimension = layer_dimension[i]
    weight = get_weight([in_dimension, out_dimension], 0.003)
    bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
    cur_layer = tf.nn.elu(tf.matmul(cur_layer, weight) + bias)
    in_dimension = layer_dimension[i]

y= cur_layer

# 损失函数的定义。
mse_loss = tf.reduce_sum(tf.pow(y_ - y, 2)) / sample_size
tf.add_to_collection('losses', mse_loss)
loss = tf.add_n(tf.get_collection('losses'))

4. 训练不带正则项的损失函数mse_loss

# 定义训练的目标函数mse_loss，训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
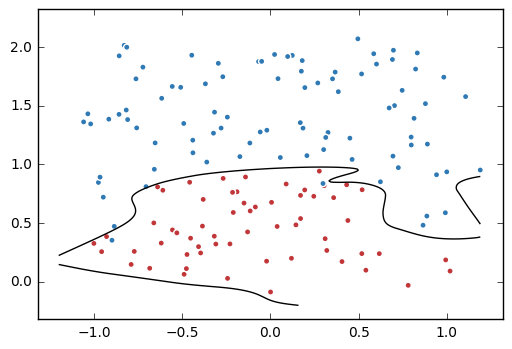
            print("After %d steps, mse_loss: %f" % (i,sess.run(mse_loss, feed_dict={x: data, y_: label})))

    # 画出训练后的分割曲线
    xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()

After 0 steps, mse_loss: 2.315934
After 2000 steps, mse_loss: 0.054761
After 4000 steps, mse_loss: 0.047252
After 6000 steps, mse_loss: 0.029857
After 8000 steps, mse_loss: 0.026388
After 10000 steps, mse_loss: 0.024671
After 12000 steps, mse_loss: 0.023310
After 14000 steps, mse_loss: 0.021284
After 16000 steps, mse_loss: 0.019408
After 18000 steps, mse_loss: 0.017947
After 20000 steps, mse_loss: 0.016683
After 22000 steps, mse_loss: 0.015700
After 24000 steps, mse_loss: 0.014854
After 26000 steps, mse_loss: 0.014021
After 28000 steps, mse_loss: 0.013597
After 30000 steps, mse_loss: 0.013161
After 32000 steps, mse_loss: 0.012915
After 34000 steps, mse_loss: 0.012671
After 36000 steps, mse_loss: 0.012465
After 38000 steps, mse_loss: 0.012251

5. 训练带正则项的损失函数loss。

# 定义训练的目标函数loss，训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
            print("After %d steps, loss: %f" % (i, sess.run(loss, feed_dict={x: data, y_: label})))

    # 画出训练后的分割曲线
    xx, yy = np.mgrid[-1:1:.01, 0:2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()

After 0 steps, loss: 2.468601
After 2000 steps, loss: 0.111190
After 4000 steps, loss: 0.079666
After 6000 steps, loss: 0.066808
After 8000 steps, loss: 0.060114
After 10000 steps, loss: 0.058860
After 12000 steps, loss: 0.058358
After 14000 steps, loss: 0.058301
After 16000 steps, loss: 0.058279
After 18000 steps, loss: 0.058266
After 20000 steps, loss: 0.058260
After 22000 steps, loss: 0.058255
After 24000 steps, loss: 0.058243
After 26000 steps, loss: 0.058225
After 28000 steps, loss: 0.058208
After 30000 steps, loss: 0.058196
After 32000 steps, loss: 0.058187
After 34000 steps, loss: 0.058181
After 36000 steps, loss: 0.058177
After 38000 steps, loss: 0.058174

3、滑动平均模型

可以使模型有更好的表现

1. 定义变量及滑动平均类

import tensorflow as tf
v1 = tf.Variable(0, dtype=tf.float32)
step = tf.Variable(0, trainable=False)
ema = tf.train.ExponentialMovingAverage(0.99, step)
maintain_averages_op = ema.apply([v1]) 

2. 查看不同迭代中变量取值的变化。

with tf.Session() as sess:

    # 初始化
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print sess.run([v1, ema.average(v1)])

    # 更新变量v1的取值
    sess.run(tf.assign(v1, 5))
    sess.run(maintain_averages_op)
    print sess.run([v1, ema.average(v1)]) 

    # 更新step和v1的取值
    sess.run(tf.assign(step, 10000))
    sess.run(tf.assign(v1, 10))
    sess.run(maintain_averages_op)
    print sess.run([v1, ema.average(v1)])       

    # 更新一次v1的滑动平均值
    sess.run(maintain_averages_op)
    print sess.run([v1, ema.average(v1)]) 

[0.0, 0.0]
[5.0, 4.5]
[10.0, 4.5549998]
[10.0, 4.6094499]