Python-求解两个字符串的最长公共子序列

一、问题描述

给定两个字符串，求解这两个字符串的最长公共子序列（Longest Common Sequence）。比如字符串1：BDCABA；字符串2：ABCBDAB。则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

二、算法求解

这是一个动态规划的题目。对于可用动态规划求解的问题，一般有两个特征：①最优子结构；②重叠子问题

①最优子结构

设X=(x₁,x₂,...,x_n)和Y=(y₁,y₂,...,y_m)是两个序列，将X和Y的最长公共子序列记为LCS(X,Y)

找出LCS(X,Y)就是一个最优化问题。因为，我们需要找到X和Y中最长的那个公共子序列。而要找X和Y的LCS，首先考虑X的最后一个元素和Y的最后一个元素。

⑴如果x_n=y_m，即X的最后一个元素与Y的最后一个元素相同，这说明该元素一定位于公共子序列中。因此，现在只需要找：LCS(X_n-1,Y_m-1)

LCS(X_n-1,Y_m-1)就是原问题的一个子问题。为什么叫子问题？因为它的规模比原问题小。

为什么是最优的子问题？因为我们要找的是X_n-1和Y_m-1的最长公共子序列啊。最长的！换句话说就是最优的那个。

⑵如果x_n!=y_m，这下要麻烦一点，因为它产生了两个子问题：LCS(X_n-1,Y_m)和LCS(X_n,Y_m-1)

因为序列X和序列Y的最后一个元素不相等，那说明最后一个元素不可能是最长公共子序列中的元素。

LCS(X_n-1,Y_m)表示：最长公共序列可以在(x₁,x₂,...x_n-1)和(y₁,y₂,...,y_m)中找。

LCS(X_n,Y_m-1)表示：最长公共序列可以在(x₁,x₂,...x_n)和(y₁,y₂,...,y_m-1)中找。

求解上面两个子问题，得到的公共子序列谁最长，那谁就是LCS(X,Y)。用数学表示就是：

LCS=max{LCS(X_n-1,Y_m),LCS(X_n,Y_m-1)}

由于条件⑴和⑵考虑到了所有可能的情况。因此，我们成功的把原问题转化成了三个规模更小的问题。

②重叠子问题

重叠子问题是什么？就是说原问题转化成子问题后，子问题中有相同的问题。

原问题是：LCS(X,Y)。子问题有❶LCS(X_n-1,Y_m-1)❷ LCS(X_n-1,Y_m)❸ LCS(X_n,Y_m-1)

乍一看，这三个问题是不重叠的。可本质上它们是重叠的，因为它们只重叠了一大部分。举例：

第二个子问题：LCS(X_n-1,Y_m)就包含了问题❶LCS(X_n-1,Y_m-1)，为什么？

因为，当X_n-1和Y_m的最后一个元素不相同时，我们又需要将LCS(X_n-1,Y_m-1)进行分解：分解成：LCS(X_n-1,Y_m-1)和LCS(X_n-2,Y_m)

也就是说：在子问题的继续分解中，有些问题是重叠的。

由于像LCS这样的问题，它具有重叠子问题的性质，因此：用递归来求解就太不划算了。国为采用递归，它重复地求解了子问题，而且需要注意的是，所有子问题加起来的个数是指数级的。

那么问题来了，如果用递归求解，有指数级个子问题，故时间复杂度是指数级的。这指数级个子问题，难道用了动态规划，就变成多项式时间了？？

关键是采用动态规划时，并不需要去一一计算那些重叠了的子问题。或者说：用了动态规划之后，有些子问题是通过“查表”直接得到的，而不是重新又计算一遍得到的。举个例子：比如求Fib数列。

求fib(5)，分解成了两个子问题：fib(4)和fib(3)，求解fib(4)和fib(3)时，又分解了一系列的小问题...

从图中可以看出：根的左右子树：fib(4)和fib(3)下，是有很多重叠的！比如，对于fib(2)，它就一共出现了三次。如果用递归来求解，fib(2)就会被计算三次，而用DP（Dynamic Programming）动态规划，则fib(2)只会计算一次，其他两次则是通过“查表”直接求得。而且，更关键的是：查找求得该问题的解之后，就不需要再继续去分解该问题了。而对于递归，是不断地将问题解，直到分解为基准问题（fib(0)或者fib(1)）

说了这么多，还是写下最长公共子序列的递归式才完整。

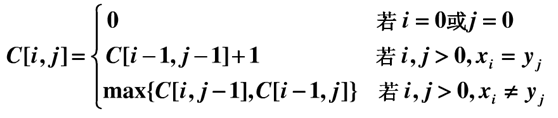
C[i,j]表示：(x₁,x₂,...,x_i)和(y₁,y₂,...,y_j)的最长公共子序列的长度。公式的具体解释可参考《算法导论》动态规划章节

三、LCS Python代码实现

#! /usr/bin/env python3
# -*- coding:utf-8 -*-

# Author   : mayi
# Blog     : http://www.cnblogs.com/mayi0312/
# Date     : 2019/5/16
# Name     : test03
# Software : PyCharm
# Note     : 用于实现求解两个字符串的最长公共子序列

def longestCommonSequence(str_one, str_two, case_sensitive=True):
    """
    str_one 和 str_two 的最长公共子序列
    :param str_one: 字符串1
    :param str_two: 字符串2（正确结果）
    :param case_sensitive: 比较时是否区分大小写，默认区分大小写
    :return: 最长公共子序列的长度
    """
    len_str1 = len(str_one)
    len_str2 = len(str_two)
    # 定义一个列表来保存最长公共子序列的长度，并初始化
    record = [[0 for i in range(len_str2 + 1)] for j in range(len_str1 + 1)]
    for i in range(len_str1):
        for j in range(len_str2):
            if str_one[i] == str_two[j]:
                record[i + 1][j + 1] = record[i][j] + 1
            elif record[i + 1][j] > record[i][j + 1]:
                record[i + 1][j + 1] = record[i + 1][j]
            else:
                record[i + 1][j + 1] = record[i][j + 1]

    return record[-1][-1]

if __name__ == '__main__':
    # 字符串1
    s1 = "BDCABA"
    # 字符串2
    s2 = "ABCBDAB"
    # 计算最长公共子序列的长度
    res = longestCommonSequence(s1, s2)
    # 打印结果
    print(res) #