GBDT总结

一、简介

gbdt全称梯度下降树，在传统机器学习算法里面是对真实分布拟合的最好的几种算法之一，在前几年深度学习还没有大行其道之前，gbdt在各种竞赛是大放异彩。原因大概有几个，一是效果确实挺不错。二是即可以用于分类也可以用于回归。三是可以筛选特征。这三点实在是太吸引人了，导致在面试的时候大家也非常喜欢问这个算法。 gbdt的面试考核点，大致有下面几个:

• gbdt 的算法的流程？
• gbdt 如何选择特征 ？
• gbdt 如何构建特征 ？
• gbdt 如何用于分类？
• gbdt 通过什么方式减少误差 ？
• gbdt的效果相比于传统的LR，SVM效果为什么好一些 ？
• gbdt 如何加速训练？
• gbdt的参数有哪些，如何调参 ？
• gbdt 实战当中遇到的一些问题 ？
• gbdt的优缺点 ？

几个误区：

• 树的个数就是最大迭代次数，与分类类别无关
• 实际计算的残差 = 样本i对应类别k的真实概率 - 上一轮预测的概率
• 多分类问题每棵树都是多类别分类器

• GBDT算法基树采用CART回归树（回归、分析用的都是回归树），树节点的划分指标是平方损失函数，叶子节点的值是落在该叶子节点所有样本的目标均值。树与树之间的Boosting逻辑是：新树拟合的目标是上一课树的损失函数的负梯度的值。GBDT最终的输出结果是将样本在所有树上的叶子值相加。可以看出，GBDT最核心的两部分，Boosting 提升说明每棵树之间是有关系有序的、Gradient梯度指明了提升的方向与大小。

1. gbdt的训练过程

　　gbdt通过多轮迭代,每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单，并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度。弱分类器一般会选择为CART TREE（也就是分类回归树）。由于上述高偏差和简单的要求每个分类回归树的深度不会很深。最终的总分类器是将每轮训练得到的弱分类器加权求和得到的（也就是加法模型）。

　　模型最终可以描述为：

　　模型一共训练M轮，每轮产生一个弱分类器 T(x;θm)。弱分类器的损失函数

　　Fm−1(x) 为当前的模型，gbdt 通过经验风险极小化来确定下一个弱分类器的参数。具体到损失函数本身的选择也就是L的选择，有平方损失函数，0-1损失函数，对数损失函数等等。如果我们选择平方损失函数，那么这个差值其实就是我们平常所说的残差。

• 但是其实我们真正关注的，1.是希望损失函数能够不断的减小，2.是希望损失函数能够尽可能快的减小。所以如何尽可能快的减小呢？

• 让损失函数沿着梯度方向的下降。这个就是gbdt 的 gb的核心了。利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值去拟合一个回归树。gbdt 每轮迭代的时候，都去拟合损失函数在当前模型下的负梯度。

• 这样每轮训练的时候都能够让损失函数尽可能快的减小，尽快的收敛达到局部最优解或者全局最优解。

2. gbdt 如何选择特征 ？

gbdt选择特征的细节其实是想问你CART Tree生成的过程。这里有一个前提，gbdt的弱分类器默认选择的是CART TREE。其实也可以选择其他弱分类器的，选择的前提是低方差和高偏差。框架服从boosting 框架即可。

下面我们具体来说CART TREE(是一种二叉树) 如何生成。CART TREE 生成的过程其实就是一个选择特征的过程。假设我们目前总共有 M 个特征。第一步我们需要从中选择出一个特征 j，做为二叉树的第一个节点。然后对特征 j 的值选择一个切分点 m. 一个 样本的特征j的值 如果小于m，则分为一类，如果大于m,则分为另外一类。如此便构建了CART 树的一个节点。其他节点的生成过程和这个是一样的。现在的问题是在每轮迭代的时候，如何选择这个特征 j,以及如何选择特征 j 的切分点 m:

• 原始的gbdt的做法非常的暴力，首先遍历每个特征，然后对每个特征遍历它所有可能的切分点，找到最优特征 m 的最优切分点 j。
• 如何衡量我们找到的特征 m和切分点 j 是最优的呢？ 我们用定义一个函数 FindLossAndSplit 来展示一下求解过程：
• 我们先遍历训练样本的所有的特征，对于特征 j，我们遍历特征 j 所有特征值的切分点 c。找到可以让下面这个式子最小的特征 j 以及切分点c.

3. gbdt 如何构建特征 ？

　　其实说gbdt 能够构建特征并非很准确，gbdt 本身是不能产生特征的，但是我们可以利用gbdt去产生特征的组合。在CTR预估中，工业界一般会采用逻辑回归去进行处理,在我的上一篇博文当中已经说过，逻辑回归本身是适合处理线性可分的数据，如果我们想让逻辑回归处理非线性的数据，其中一种方式便是组合不同特征，增强逻辑回归对非线性分布的拟合能力。

长久以来，我们都是通过人工的先验知识或者实验来获得有效的组合特征，但是很多时候，使用人工经验知识来组合特征过于耗费人力，造成了机器学习当中一个很奇特的现象：有多少人工就有多少智能。关键是这样通过人工去组合特征并不一定能够提升模型的效果。所以我们的从业者或者学界一直都有一个趋势便是通过算法自动，高效的寻找到有效的特征组合。Facebook 在2014年 发表的一篇论文便是这种尝试下的产物，利用gbdt去产生有效的特征组合，以便用于逻辑回归的训练，提升模型最终的效果。

　　如上图所示，我们 使用 GBDT 生成了两棵树，两棵树一共有五个叶子节点。我们将样本 X 输入到两颗树当中去，样本X 落在了第一棵树的第二个叶子节点，第二棵树的第一个叶子节点，于是我们便可以依次构建一个五维的特征向量，每一个维度代表了一个叶子节点，样本落在这个叶子节点上面的话那么值为1，没有落在该叶子节点的话，那么值为 0.

　　于是对于该样本，我们可以得到一个向量[0,1,0,1,0] 作为该样本的组合特征，和原来的特征一起输入到逻辑回归当中进行训练。实验证明这样会得到比较显著的效果提升。

4. gbdt 如何用于分类？

　　首先明确一点，gbdt 无论用于分类还是回归一直都是使用的CART 回归树。不会因为我们所选择的任务是分类任务就选用分类树，这里面的核心是因为gbdt 每轮的训练是在上一轮的训练的残差基础之上进行训练的。这里的残差就是当前模型的负梯度值 。这个要求每轮迭代的时候，弱分类器的输出的结果相减是有意义的。残差相减是有意义的。

如果选用的弱分类器是分类树，类别相减是没有意义的。上一轮输出的是样本 x 属于 A类，本一轮训练输出的是样本 x 属于 B类。 A和B很多时候甚至都没有比较的意义，A类-B类是没有意义的。

我们具体到分类这个任务上面来，我们假设样本 X 总共有 K类。来了一个样本 x，我们需要使用gbdt来判断 x 属于样本的哪一类。

　　第一步 我们在训练的时候，是针对样本 X 每个可能的类都训练一个分类回归树。举例说明，目前样本有三类，也就是 K = 3。样本 x 属于 第二类。那么针对该样本 x 的分类结果，其实我们可以用一个 三维向量 [0,1,0] 来表示。0表示样本不属于该类，1表示样本属于该类。由于样本已经属于第二类了，所以第二类对应的向量维度为1，其他位置为0。

针对样本有 三类的情况，我们实质上是在每轮的训练的时候是同时训练三棵树。第一棵树针对样本x的第一类，输入为（x,0）。第二棵树输入针对样本x的第二类，输入为（x,1）。第三颗树针对样本x 的第三类，输入为（x，0）

在这里每棵树的训练过程其实就是就是我们之前已经提到过的CATR TREE 的生成过程。在此处我们参照之前的生成树的程序 即可以解出三棵树，以及三棵树对x 类别的预测值f1(x),f2(x),f3(x)。那么在此类训练中，我们仿照多分类的逻辑回归 ，使用softmax 来产生概率，则属于类别 1 的概率

　　并且我们我们可以针对类别1 求出 残差y1(x)=0−p1(x);类别2 求出残差y2(x)=1−p2(x);类别3 求出残差y3(x)=0−p3(x).

然后开始第二轮训练 针对第一类 输入为（x,y1(x)）, 针对第二类输入为（x,y2(x))), 针对 第三类输入为 (x,y3(x)).继续训练出三棵树。一直迭代M轮。每轮构建 3棵树。

所以当K =3，我们其实应该有三个式子

　　当训练完毕以后，新来一个样本 x1 ，我们需要预测该样本的类别的时候，便可以有这三个式子产生三个值，f1(x),f2(x),f3(x)。样本属于 某个类别c的概率为

GBDT多分类举例

这是一个有6个样本的三分类问题。我们需要根据这个花的花萼长度，花萼宽度，花瓣长度，花瓣宽度来判断这个花属于山鸢尾，杂色鸢尾，还是维吉尼亚鸢尾。具体应用到gbdt多分类算法上面。我们用一个三维向量来标志样本的label。[1,0,0] 表示样本属于山鸢尾，[0,1,0] 表示样本属于杂色鸢尾，[0,0,1] 表示属于维吉尼亚鸢尾。

gbdt 的多分类是针对每个类都独立训练一个 CART Tree。所以这里，我们将针对山鸢尾类别训练一个 CART Tree 1。杂色鸢尾训练一个 CART Tree 2 。维吉尼亚鸢尾训练一个CART Tree 3，这三个树相互独立。

我们以样本 1 为例。针对 CART Tree1 的训练样本是[5.1,3.5,1.4,0.2][5.1,3.5,1.4,0.2]，label 是 1，最终输入到模型当中的为[5.1,3.5,1.4,0.2,1][5.1,3.5,1.4,0.2,1]。针对 CART Tree2 的训练样本也是[5.1,3.5,1.4,0.2][5.1,3.5,1.4,0.2],但是label 为 0,最终输入模型的为[5.1,3.5,1.4,0.2,0][5.1,3.5,1.4,0.2,0]. 针对 CART Tree 3的训练样本也是[5.1,3.5,1.4,0.2][5.1,3.5,1.4,0.2],label 也为0,最终输入模型当中的为[5.1,3.5,1.4,0.2,0][5.1,3.5,1.4,0.2,0].

下面我们来看 CART Tree1 是如何生成的，其他树 CART Tree2 , CART Tree 3的生成方式是一样的。CART Tree的生成过程是从这四个特征中找一个特征做为CART Tree1 的节点。比如花萼长度做为节点。6个样本当中花萼长度 大于5.1 cm的就是 A类，小于等于 5.1 cm 的是B类。生成的过程其实非常简单，问题 1.是哪个特征最合适？ 2.是这个特征的什么特征值作为切分点？ 即使我们已经确定了花萼长度做为节点。花萼长度本身也有很多值。在这里我们的方式是遍历所有的可能性，找到一个最好的特征和它对应的最优特征值可以让当前式子的值最小。

我们以第一个特征的第一个特征值为例。R1 为所有样本中花萼长度小于 5.1 cm 的样本集合，R2 为所有样本当中花萼长度大于等于 5.1cm 的样本集合。所以 R1={2}R1={2}，R2={1,3,4,5,6}R2={1,3,4,5,6}.

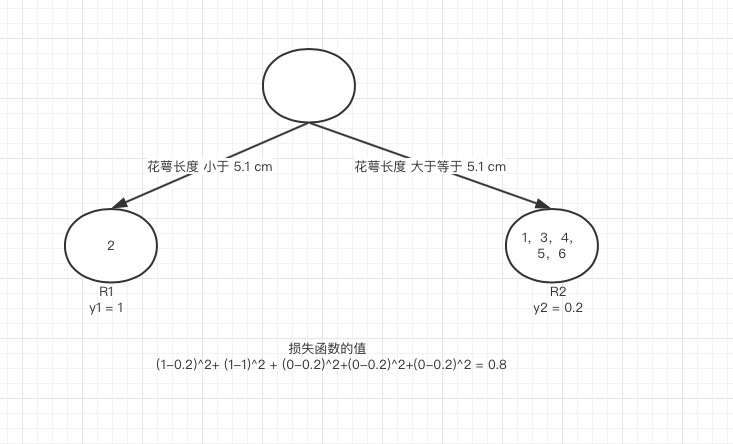
y1 为 R1 所有样本的label 的均值 1/1=1。y2 为 R2 所有样本的label 的均值 (1+0+0+0+0)/5=0.2。

下面便开始针对所有的样本计算这个式子的值。样本1 属于 R2 计算的值为(1−0.2)2(1−0.2)2, 样本2 属于R1 计算的值为(1−1)2(1−1)2, 样本 3，4，5，6同理都是 属于 R2的 所以值是(0−0.2)2(0−0.2)2. 把这六个值加起来，便是 山鸢尾类型在特征1 的第一个特征值的损失值。这里算出来(1-0.2)^2+ (1-1)^2 + (0-0.2)^2+(0-0.2)^2+(0-0.2)^2 +(0-0.2)^2= 0.84

接着我们计算第一个特征的第二个特征值，计算方式同上，R1 为所有样本中 花萼长度小于 4.9 cm 的样本集合，R2 为所有样本当中 花萼长度大于等于 4.9 cm 的样本集合.所以 R1={}，R1={1,2,3,4,5,6}. y1 为 R1 所有样本的label 的均值 = 0。y2 为 R2 所有样本的label的值 (1+1+0+0+0+0)/6=0.3333。

　　我们需要针对所有的样本,样本1 属于 R2, 计算的值为(1−0.333)^2, 样本2 属于R2 ,计算的值为(1−0.333)^2, 样本 3，4，5，6同理都是 属于 R2的, 所以值是(0−0.333)^2. 把这六个值加起来山鸢尾类型在特征1 的第二个特征值的损失值。这里算出来 (1-0.333)^2+ (1-0.333)^2 + (0-0.333)^2+(0-0.333)^2+(0-0.333)^2 +(0-0.333)^2 = 2.244189. 这里的损失值大于 特征一的第一个特征值的损失值，所以我们不取这个特征的特征值。

这样我们可以遍历所有特征的所有特征值，找到让这个式子最小的特征以及其对应的特征值，一共有24种情况,4个特征*每个特征有6个特征值。在这里我们算出来让这个式子最小的特征花萼长度,特征值为5.1 cm。这个时候损失函数最小为 0.8。

于是我们的预测函数此时也可以得到

　　此处 R1 = {2},R2 = {1,3,4,5,6}，y1 = 1,y2 = 0.2。训练完以后的最终式子为

　　由这个式子，我们得到对样本属于类别1 的预测值 f1(x)=1+0.2∗5=2。同理我们可以得到对样本属于类别2,3的预测值f2(x),f3(x)。样本属于类别1的概率即为 

5. gbdt如何用于回归？

　　（当损失函数不为square loss时残差并不一定等于负梯度）。我们实际上是在通过梯度下降法对模型参数进行更新。这样理解的好处在于我们可以把这一算法推广到其他的损失函数上。

　　要注意regression并不一定会用square loss。 square loss的优点是便于理解和实现，缺点在于对于异常值它的鲁棒性较差，如下图：

　　一个异常值造成的损失由于二次幂而被过分放大，会影响到最后得到模型在测试集上的表现。因此，我们有时候会选择其他的损失函数，如absolute loss或Huber loss（标红色星号的数据为异常值）：

　　梯度下降法的思想使得我们可以非常轻易地改用不同的损失函数设计Gradient Boosting算法。另外在使用某些其他损失函数时（如Huber loss），残差相比负梯度更容易受到异常值的影响。

6. gbdt 通过什么方式减少误差 ？

每棵树都是在拟合当前模型的预测值和真实值之间的误差，GBDT是通过不断迭代来使得误差见小的过程。

7. gbdt的效果相比于传统的LR，SVM效果为什么好一些 ？

GBDT基于树模型，继承了树模型的优点 [对异常点鲁棒、不相关的特征干扰性低（LR需要加正则）、可以很好地处理缺失值、受噪音的干扰小]

8. gbdt 如何加速训练？

对于小数据集，是否预排序选项选True，预排序可以加速查找最佳分裂点

9. gbdt的参数有哪些，如何调参 ？

参数分为三类
第一类：Miscellaneous Parameters: Other parameters for overall functioning. 没啥用
第二类：Boosting Parameters: These affect the boosting operation in the model.
n_estimators 最大弱学习器的个数，太小欠拟合，太大过拟合
learning_rate 学习率，太大过拟合，一般很小0.1，和n_estimators一起调
subsample 子采样，防止过拟合，太小欠拟合。GBDT中是不放回采样
第三类：Tree-Specific Parameters: These affect each individual tree in the model.
max_features 最大特征数
max_depth 最大树深，太大过拟合
min_samples_split 内部节点再划分所需最小样本数，越大越防过拟合
min_weight_fraction_leaf 叶子节点最小的样本权重和。如果存在较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。越大越防过拟合
max_leaf_nodes:最大叶子节点数 ，太大过拟合
min_impurity_split:节点划分最小不纯度
presort:是否对数据进行预分类，以加快拟合中最佳分裂点的发现。默认False，适用于大数据集。小数据集使用True,可以加快训练。是否预排序,预排序可以加速查找最佳分裂点，对于稀疏数据不管用，Bool，auto：非稀疏数据则预排序，若稀疏数据则不预排序

接下来把调参的整个过程整理一下：

• 首先使用默认的参数，进行数据拟合；
• 从步长(learning rate)和迭代次数(n_estimators)入手；一般来说,开始选择一个较小的步长来网格搜索最好的迭代次数。这里，可以将步长初始值设置为0.1。对于迭代次数进行网格搜索；
• 接下来对决策树的参数进行寻优
• 首先我们对决策树最大深度max_depth和内部节点再划分所需最小样本数min_samples_split进行网格搜索。【min_samples_split暂时不能一起定下来，因为这个还和决策树其他的参数存在关联】
• 接着再对内部节点再划分所需最小样本数min_samples_split和叶子节点最少样本数min_samples_leaf一起调参；做到这里，min_samples_split要做两次网格寻优，一次是树的最大深度max_depth，一次是叶子节点最少样本数min_samples_leaf。 【具体观察min_samples_split的值是否落在边界上，如果是可以进一步寻优】
• 继续对最大特征数max_features进行网格搜索。做完这一步可以看看寻找出的最优参数组合给出的分类器的效果。
• 可以进一步考虑对子采样的比例进行网格搜索，得到subsample的寻优参数
• 回归到第2步调整设定的步长(learning rate)和迭代次数(n_estimators)，注意两者的乘积保持不变，这里可以分析得到：通过减小步长可以提高泛化能力，但是步长设定过小，也会导致拟合效果反而变差，也就是说，步长不能设置的过小。

10. gbdt 的正则化

• Early Stopping，本质是在某项指标达标后就停止训练，也就是设定了训练的轮数；
• Shrinkage，其实就是学习率，具体做法是将没课树的效果进行缩减，比如说将每棵树的结果乘以0.1，也就是降低单棵树的决策权重，相信集体决策；
• Subsampling，无放回抽样，具体含义是每轮训练随机使用部分训练样本，其实这里是借鉴了随机森林的思想；
• Dropout，这个方法是论文里的方法，没有在SKLearn中看到实现，做法是每棵树拟合的不是之前全部树ensemble后的残差，而是随机挑选一些树的残差，这个效果如何有待商榷。

11. gbdt的优缺点 ？

优点：

• 可以灵活处理各种类型的数据，包括连续值和离散值。
• 在相对少的调参时间情况下，预测的准备率也可以比较高。这个是相对SVM来说的。
• 使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

缺点：由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

二、GBDT 和 随机森林/Adaboost/LR的区别与联系

1、GBDT和随机森林

相同点： 
               1、都是由多棵树组成 
               2、最终的结果都是由多棵树一起决定

不同点： 
               1、组成随机森林的树可以并行生成；而GBDT只能是串行生成 ；
               2、对于最终的输出结果而言，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来 ；
               3、随机森林对异常值不敏感，GBDT对异常值非常敏感 ；
               4、随机森林对训练集一视同仁，GBDT是基于权值的弱分类器的集成 ；
               5、随机森林是通过减少模型方差提高性能，GBDT是通过减少模型偏差提高性能；

6、随机森林既可以使用决策树也可以使用回归树，但是gbdt采用的都是CART回归树。

2、GBDT和Adaboost

和AdaBoost一样，Gradient Boosting也是重复选择一个表现一般的模型并且每次基于先前模型的表现进行调整。不同的是，AdaBoost是通过提升错分数据点的权重来定位模型的不足而Gradient Boosting是通过算梯度（gradient）来定位模型的不足。因此相比AdaBoost, Gradient Boosting可以使用更多种类的目标函数,而当目标函数是均方误差时，计算损失函数的负梯度值在当前模型的值即为残差。

3、GBDT和LR(Linear Regression? Logistic Regression?)

从决策边界来说，线性回归的决策边界是一条直线，逻辑回归的决策边界是一条曲线，而GBDT的决策边界可能是很多条线。

参考文献：

【1】机器学习算法GBDT的面试要点总结-上篇

【2】集成学习专题之GBDT面试

【3】机器学习算法中GBDT与Adaboost的区别与联系是什么？

【4】从决策树到XGBoost