字符串匹配(一)----Rabin-Karp算法

题目：假如要判断字符串A"ABA"是不是字符串B"ABABABA"的子串。

解法一：暴力破解法， 直接枚举所有的长度为3的子串，然后依次与A比较,这样就能得出匹配的位置。 这样的时间复杂度是O(M*N)，M为B的长度，N为A的长度。

解法二：Rabin-Karp算法

　　思想：假设待匹配字符串的长度为N，目标字符串的长度为M（M>N）；首先计算待匹配字符串的hash值，计算目标字符串前N个字符的hash值；比较前面计算的两个hash值，比较次数M-N+1：若hash值不相等，则继续计算目标字符串的下一个长度为N的字符子串的hash值，若hash值相同，则需要使用比较字符是否相等再次判断是否为相同的子串(这里若hash值相同，则直接可以判断待匹配字符串是目标字符串的子串，之所以需要再次判断字符是否相等，是因为不同的字符计算出来的hash值有可能相等，称之为hash冲突或hash碰撞，不过这是极小的概率，可以忽略不计)；

　　哈希函数定义如下：

　　　　其中Cm表示字符串中第m项所代表的特地数字，有很多种定义方法，我习惯于用java自带的char值，也就是ASCII码值。java中的char是16位的，用的Unicode编码，8位的ASCII码包含在Unicode中。b是哈希函数的基数，相当于把字符串看作是b进制数。h是防止哈希值溢出。

　　　　

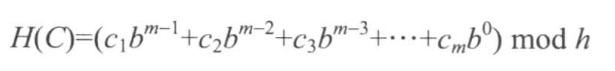
　　代码：

 public class RabinKarp {

     public static void main(String[] args) {
         String s = "ABABABA";
         String p = "ABA";
         match(p, s);
     }

     /**
      * @param p 模式
      * @param s 源串
      */
     static void match(String p,String s){
         long hash_p = hash(p);//p的hash值
         int p_len = p.length();
         for (int i = 0; i+p_len<= s.length(); i++) {
             long hash_i = hash(s.substring(i, i+p_len));// i 为起点，长度为p_len的子串的hash值
             if (hash_p==hash_i) {
                 System.out.println("match:"+i);
             }
         }
     }

     final static long seed = 31;  // 进制数

     /**
      * 不同的字符计算出来的hash值相同 称为hash冲突
      * 使用100000个不同字符串产生的冲突数，大概在0~3波动，使用100百万不同的字符串，冲突数大概110+范围波动。
      * @param str
      * @return
      */
     private static long hash(String str) {
         long h = 0;
         for (int i = 0; i !=str.length(); i++) {
             // 这个计算方式就是 An²+Bn+c 的循环表达式，而这个计算方式就是二进制转十进制的计算方式
             // 这里n=31，可以理解为转为31进制
             h = seed * h + str.charAt(i);

         }
         return h%Long.MAX_VALUE;  // 防止hash值过大
     }

 }

　　结果：

　　　　

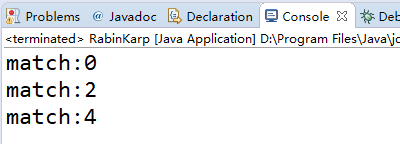
　　在这里计算一下时间复杂度，计算hash值的时间为O(N)，目标字符串长度为M，所以时间复杂度为O(M*N)。好像和暴力破解差不多。下面会通过一种类似于预处理的方式来进行优化，叫做滚动哈希。就是提前计算好源串的hash值，构建成一个hash数组，再通过比较hash值，这样就成功匹配出来了。通过这种优化，时间复杂度下降到O(M+N),O(N)为计算待匹配的字符串计算hash值的时间，O(M)为计算hash数组的时间。

　　滚动哈希的技巧就是：如果已经算出从k到k+m的子串的哈希值H(S[k,k+1...k+m])，那么从k+1到k+m+1的子串的哈希值就可以基于前一个的哈希值计算得出。

　　　　

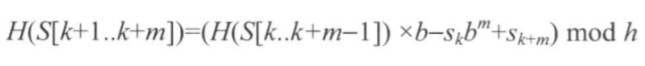
　　代码：

 /**
  * 滚动哈希法
  * 对目标字符串按d进制求值，mod h 取余作为其hash
  * 对源串，一次求出m个字符的hash，保存在数组中(滚动计算)
  * 匹配时，只需对比目标串的hash值和预存的源串的hash值表
  */
 public class RabinKarp_1 {

     public static void main(String[] args) {
         String s = "ABABABA";
         String p = "ABA";
         match(p, s);
     }

     static void match(String p,String s){
         long hash_p = hash(p);//p的hash值
         long[] hashOfS = hash(s, p.length());
         for (int i = 0; i < hashOfS.length; i++) {
             if (hashOfS[i] == hash_p) {
                 System.out.println("match:" + i);
             }
         }
     }

     final static long seed = 31;

     /**
      * 滚动哈希
      * @param s 源串
      * @param n 子串的长度
      * @return
      */
     private static long[] hash(String s, int n) {
         long[] res = new long[s.length() - n + 1];
         //前n个字符的hash
         res[0] = hash(s.substring(0, n));
         for (int i = n; i < s.length(); i++) {
           char newChar = s.charAt(i);  // 新增的字符
           char oldchar = s.charAt(i - n);  // 前n字符的第一字符
           //前n个字符的hash*seed-前n字符的第一字符*seed的n次方
           long v = (long) ((res[i - n] * seed + newChar - Math.pow(seed, n) * oldchar) % Long.MAX_VALUE);
           res[i - n + 1] = v;
         }
         return res;
     }

     static long hash(String str) {
         long h = 0;
         for (int i = 0; i != str.length(); ++i) {
           h = seed * h + str.charAt(i);
         }
         return h % Long.MAX_VALUE;
       }
 }

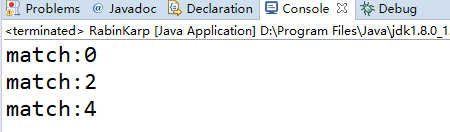
　　结果：