Morris 遍历实现二叉树的遍历

Morris 遍历实现二叉树的遍历

作者：Grey

原文地址：

博客园：Morris 遍历实现二叉树的遍历

CSDN：Morris 遍历实现二叉树的遍历

说明

Morris 遍历可以实现二叉树的先，中，后序遍历，且时间复杂度O(N), 空间复杂度可以做到O(1)。

Morris 遍历流程

假设有一棵如下的二叉树

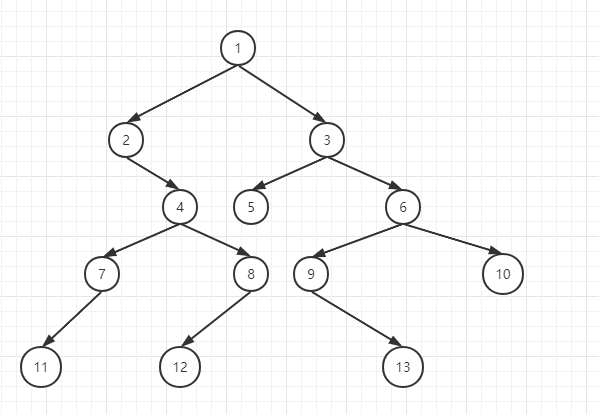
Morris遍历的流程主要分如下几个步骤：

第一步，从头节点开始遍历。

第二步，假设当前遍历的节点是cur。

第三步，如果cur无左树, cur来到其右树上，即：cur = cur.right

第四步，如果cur有左树，找到cur左树最右节点，假设叫mostRight，则有如下两种小情况：

情况1，如果mostRight的右指针指向空, 则将mostRight的右指针指向cur，即：mostRight.right = cur, 然后将cur向左移动，即：cur = cur.left，

情况2，如果mostRight的右指针指向当前节点cur，则将mostRight的右指针指向空，即：mostRight.right = null，然后将cur向右移动，即：cur = cur.right。

第五步：当cur = null，遍历结束。

根据如上流程，示例二叉树的Morris遍历序列为：

1-->2-->4-->7-->11-->7-->4-->8-->12-->8-->1-->3-->5-->3-->6-->9-->13-->6-->10

Morris遍历可以实现在O(N)时间复杂度内，用O(1)的空间复杂度实现对树的遍历，而且，只要某个节点有右树，则这个节点一定会被遍历两次，我们可以通过Morris遍历来实现二叉树的先，中，后序遍历，做到时间复杂度O(N)，空间复杂度O(1)。

代码实现如下：

public class Code_Morris {

    //当前是cur
    //1. cur无左树,cur = cur.right
    //2. cur有左树,找到左树最右节点mostRight
    //	a. mostRight的右指针指向null, mostRight.right = cur, cur = cur.right
    //	b. mostRight的右指针指向当前节点cur，mostRight.right = null, cur = cur.right
    //3. cur = null 停
    public static void morrisPrint(TreeNode head) {
        if (head == null) {
            return;
        }
        System.out.println("....morris order....");
        TreeNode cur = head;
        System.out.print(cur.val + "-->");
        TreeNode mostRight;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    System.out.print(cur.val + "-->");
                    continue;
                } else {
                    mostRight.right = null;
                }
            }
            cur = cur.right;
            if (cur != null) {
                System.out.print(cur.val + "-->");
            }
        }
    }
}

Morris遍历实现先序遍历

根据Morris的遍历结果，没有右树的点只会遍历一次，有右树的点会遍历两次，针对遍历一次的点，遍历到就收集，针对遍历两次的点，第一次遍历到就收集，第二次遍历到不收集，整个流程跑完，则得到了先序遍历的结果。

代码如下：

    public static List<Integer> preorderTraversal(TreeNode root) {
        if (null == root) {
            return new ArrayList<>();
        }
        List<Integer> ans = new ArrayList<>();
        TreeNode mostRight;
        TreeNode cur = root;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    // 有右树，第一次来到自己就收集
                    ans.add(cur.val);
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    // mostRight.right = cur;
                    mostRight.right = null;
                }
            } else {
                // 没有右树的，来到就收集
                ans.add(cur.val);
            }
            cur = cur.right;
        }
        return ans;
    }

测评链接：LeetCode 144. Binary Tree Preorder Traversal

Morris遍历实现中序遍历

针对遍历一次的点，遍历到就收集，针对遍历两次的点，第一次遍历到不收集，第二次遍历才收集，整个流程跑完，则得到了中序遍历的结果。

代码如下：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> ans = new ArrayList<>();
        TreeNode mostRight;
        TreeNode cur = root;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    // 来到自己两次的点，第二次来到才收集
                    ans.add(cur.val);
                    mostRight.right = null;
                }
            } else {
                // 只来到自己一次的点，来到就收集
                ans.add(cur.val);
            }
            cur = cur.right;
        }
        return ans;
    }
}

测评链接：LeetCode 94. Binary Tree Inorder Traversal

Morris遍历实现后序遍历

Morris遍历实现后序遍历相对比较麻烦，处理时机只放在能回到自己两次的点，能回到自己两次的点在第二次回到自己的时刻，不打印它自己，而是逆序打印他左树的右边界, 整个遍历结束后，单独逆序打印整棵树的右边界，即得到了后序遍历的结果。

代码如下：

    public List<Integer> postorderTraversal(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        List<Integer> ans = new ArrayList<>();
        TreeNode cur = root;
        TreeNode mostRight;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                    // 第二次来到自己的时候，收集自己的左树的右边界
                    collect(cur.left, ans);
                }
            }
            cur = cur.right;
        }
        collect(root, ans);
        return ans;
    }

    private void collect(TreeNode root, List<Integer> ans) {
        TreeNode node = reverse(root);
        TreeNode c = node;
        while (c != null) {
            ans.add(c.val);
            c = c.right;
        }
        reverse(node);
    }

    private TreeNode reverse(TreeNode node) {
        TreeNode pre = null;
        TreeNode cur = node;
        while (cur != null) {
            TreeNode t = cur.right;
            cur.right = pre;
            pre = cur;
            cur = t;
        }
        return pre;
    }

需要注意两点：

第一点，collect方法即逆序收集左树的有边界，由于每个节点没有指向父的指针，所以，要实现逆序，需要针对右边界采用反转链表的方式。即reverse函数的逻辑。

第二点，在collect方法调用完反转链表操作后，还要还原整个右边界。否则整棵树的指针就指乱了。

测评链接：LeetCode 145. Binary Tree Postorder Traversal

更多

算法和数据结构笔记

参考资料

算法和数据结构体系班-左程云