KMeans算法与GMM混合高斯聚类

一、K-Means

K-Means是GMM的特例（硬聚类，基于原型的聚类）。假设多元高斯分布的协方差为0，方差相同。

K-Means算法思想

对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

N个d维样本，时间复杂度 O(kLNd)

初始K个类（簇心）
E步：对每个样本，计算到K个类的欧式距离，并分配类标签 O(kNd)
M步：基于类内的样本，以样本均值更新类（均值最小化，类到类内样本的误差） O(Nd)
重复2-3步，直到聚类结果不变化或收敛

迭代次数为L

收敛性证明：

聚类处理：

特征归一化，缺失值，异常值

K-Means的主要优点有：

　　1）基于原型的聚类，实现简单收敛速度快。

　　2）聚类效果较优。

　　3）算法的可解释度比较强。

　　4）主要需要调参的参数仅仅是簇数k。

K-Means的主要缺点有：

　　1）K值的选取不好把握

　　2）对于不是凸的数据集比较难收敛

　　3）如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。

　　4）采用迭代方法，得到的结果只是局部最优（本身是个NP-hard问题，组合优化，多项式系数）

　　5）对噪音和异常点比较的敏感。

# 基于Cursor生成的代码

import numpy as np

def k_means(X, k, max_iters=100):

    # randomly initialize centroids

    centroids = X[np.random.choice(range(len(X)), k, replace=False)]

    for i in range(max_iters):

        # calculate distances between each point and each centroid

        distances = np.sqrt(((X - centroids[:, np.newaxis])**2).sum(axis=2))

        # assign each point to the closest centroid

        labels = np.argmin(distances, axis=0)

        # update centroids to be the mean of the points assigned to them

        for j in range(k):

            centroids[j] = X[labels == j].mean(axis=0)

    return centroids, labels

d = 3

k = 3

X = np.random.rand(100, 3)

centroids, labels = k_means(X, k, max_iters=100)

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(10, 7))

ax = fig.add_subplot(111, projection='3d')

ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=labels, cmap='viridis')

ax.scatter(centroids[:, 0], centroids[:, 1], centroids[:, 2], marker='*', s=300, c='r')

ax.set_xlabel('X Label')

ax.set_ylabel('Y Label')

ax.set_zlabel('Z Label')

plt.show()

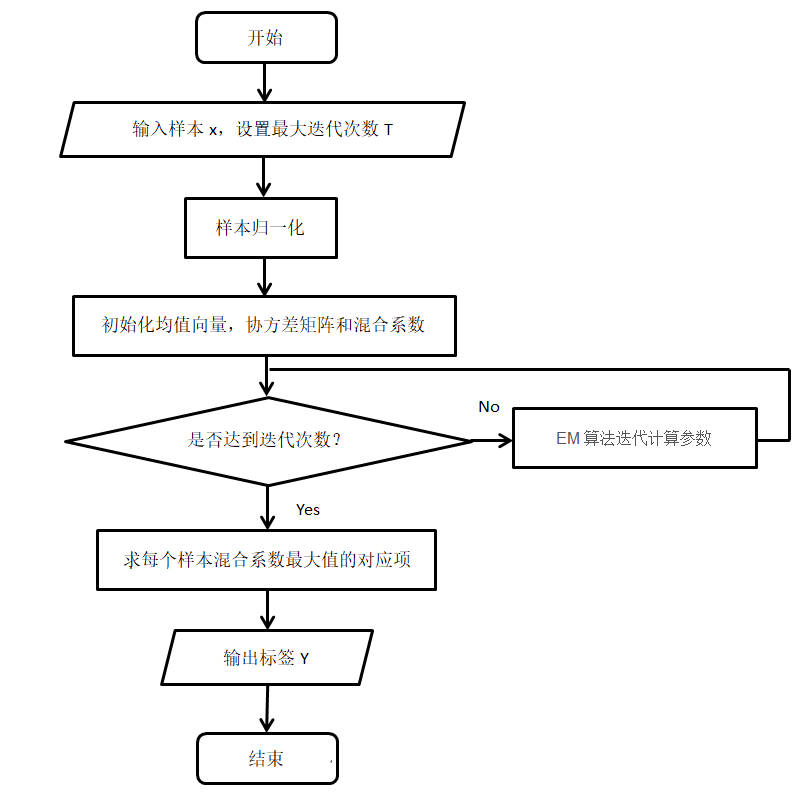
二、GMM

⾼斯分布的线性组合可以给出相当复杂的概率密度形式。

通过使⽤⾜够多的⾼斯分布，并且调节它们的均值和⽅差以及线性组合的系数，⼏乎所有的连续概率密度都能够以任意的精度近似。

对3个高斯分布的概率密度函数进行加权。考虑K个⾼斯概率密度的叠加，形式为：

混合⾼斯（mixture of Gaussians），每⼀个⾼斯概率密度N (x | µk, Σk)被称为混合分布的⼀个成分（component），并且有⾃⼰的均值µk和协⽅差Σk。

具有3个成分的混合⾼斯分布的轮廓线。参数πk被称为混合系数。GMM

可把πk = p(k)看成选择第k个成分的先验概率，把密度N (x | µk, Σk) = p(x | k)看成以k为条件的x的概率。

⾼斯混合分布的形式由参数π, µ和Σ控制，其中令π ≡ {π1, . . . , πK}, µ ≡

{µ1, . . . , µK}且Σ ≡ {Σ1, . . . , Σk}。⼀种确定这些参数值的⽅法是使⽤最⼤似然法。根据公式），对数似然函数为：

因为对数中存在⼀个求和式，导致参数的最⼤似然解不再有⼀个封闭形式的解析解：

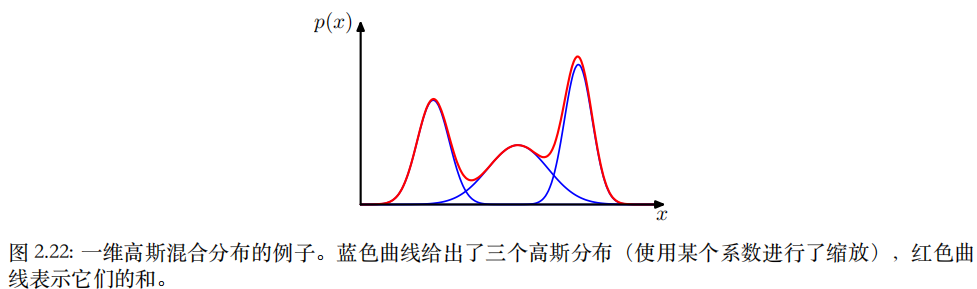
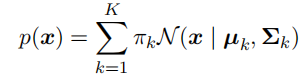
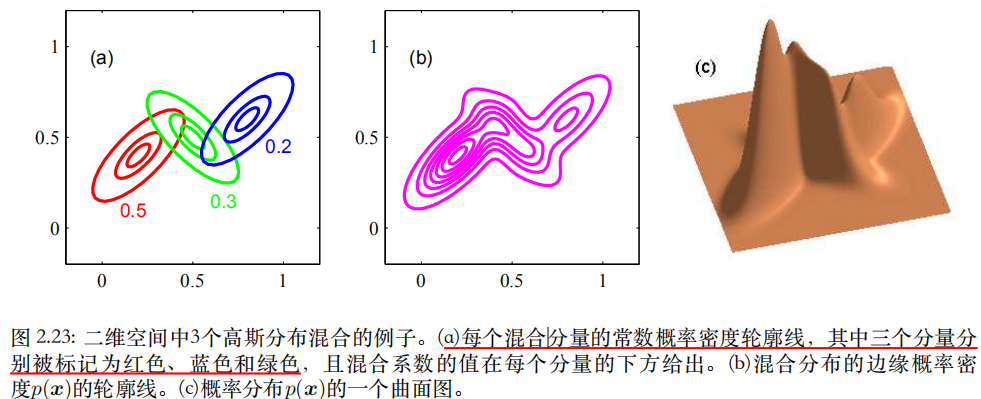
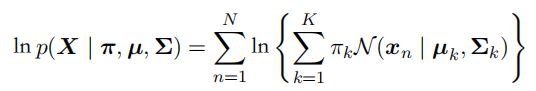
⼀种最⼤化这个似然函数的⽅法是使⽤迭代数值优化⽅法。
另⼀种是使⽤EM期望最⼤化算法(对包含隐变量的似然进行迭代优化)。

样本x为观测数据，混合系数为隐变量，高斯分布的参数。

当成分为多元高斯分布时（d维），相当于从混合多元高斯分布中生成了样本，通过EM算法迭代地学习模型参数（均值和方差以及混合系数）。

期望：根据参数，更新样本关于类的响应度（隶属度，相当于分别和K个类计算距离并归一化）。确定响应度，就可以确定EM算法的Q函数（完全数据的对数似然关于分布的期望），原始似然的下界。
最大化：根据响应度，计算均值、方差。

EM算法收敛后，直接求每个样本关于成分的响应度即可得到聚类结果（可软，可硬argmax）

当多元高斯分布的方差相同时，且每个样本只能指定给一个类时（one-hot响应度，argmax），GMM退化成K-means算法。

import numpy as np

from sklearn import datasets

import matplotlib.pyplot as plt

from sklearn.mixture import GaussianMixture

from sklearn.cluster import KMeans

# 创建数据，并可视化

X, y = datasets.make_blobs(n_samples=1500,

                             cluster_std=[1.0, 2.5, 0.5],

                             random_state=170)

plt.figure(figsize=(12,4))

plt.rcParams['font.family'] = 'STKaiti'

plt.rcParams['font.size'] = 20

plt.subplot(1,3,1)

plt.scatter(X[:,0],X[:,1],c = y)

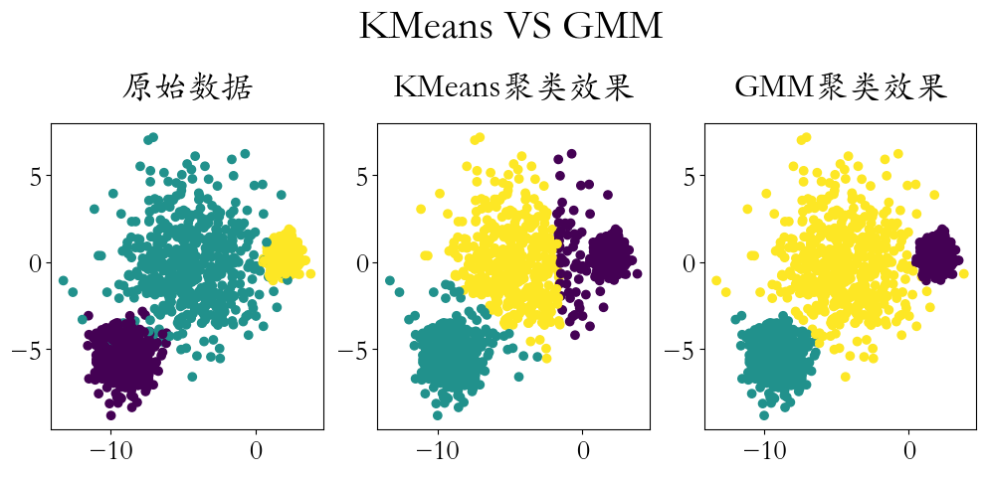
plt.title('原始数据',pad = 20)

Kmeans聚类

kmeans = KMeans(3)

kmeans.fit(X)

y_ = kmeans.predict(X)

plt.subplot(1,3,2)

plt.scatter(X[:,0],X[:,1],c = y_)

plt.title('KMeans聚类效果',pad = 20)

GMM高斯混合模型聚类

gmm = GaussianMixture(n_components=3)

y_ = gmm.fit_predict(X)

plt.subplot(1,3,3)

plt.scatter(X[:,0],X[:,1],c = y_)

plt.title('GMM聚类效果',pad = 20)

plt.figtext(x = 0.51,y = 1.1,s = 'KMeans VS GMM',ha = 'center',fontsize = 30)

plt.savefig('./GMM高斯混合模型.png',dpi = 200)

优点：

可以完成大部分形状的聚类
大数据集时，对噪声数据不敏感
对于距离或密度聚类，更适合高维特征

缺点：

计算复杂高，速度较慢
难以对圆形数据聚类
需要在测试前知道类别的个数（成分个数，超参数）
初始化参数会对聚类结果产生影响

参考

1.https://www.jianshu.com/p/2c42c567e893

2. PRML