JZOJ 4212. 【五校联考1day2】我想大声告诉你

题目

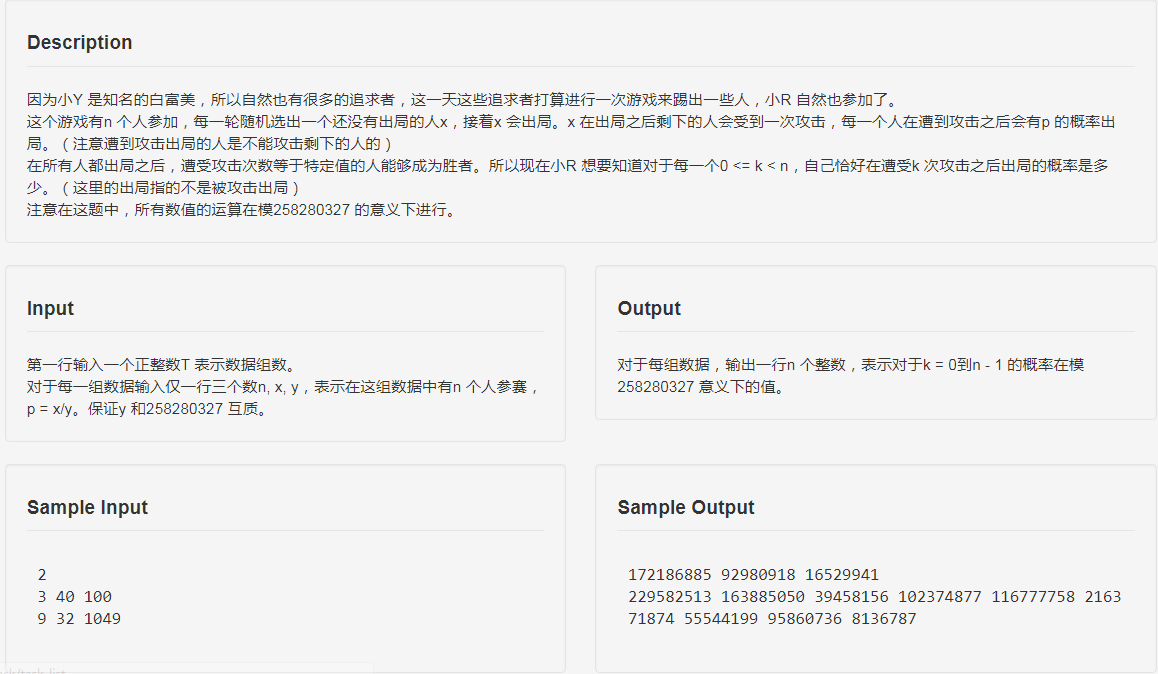
解析

设 \(f_{i,j}\) 表示 \(i+1..n\) 个人能受到 \(j\) 次攻击的概率

因为选人出局的顺序是无所谓的，所以我们设从 \(1..n\) 依次选人出局

那么转移时需要分类，分类即加

• 选第 \(i\) 个人出局，那么 \(i+1..n\) 会受到 \(1\) 次攻击。先前攻击了 \(j-1\) 次，\(i\) 必须要活下来。\(f_{i,j} = f_{i-1,j-1} \times (1-p)^{j-1}\)
• 第 \(i\) 个人是遭受攻击后被杀，那么它必然在前 \(j\) 次攻击的某一次后出局。\(f_{i,j} = f_{i-1,j} \times (1-(1-p)^j)\)

然后考虑答案是什么

对于 \(k\) 次攻击，小 \(R\) 可以是在所有的 \(f_{i,k}\) 后在被选中出局，那么他必然在受到攻击后仍活下来

所以 \(ans_k = \frac{1}{n} \times (1-p)^k \times \sum_{i=0}^n f_{i,k}\)

乘上 \(\frac{1}{n}\) 是因为小 \(R\) 有 \(\frac{1}{n}\) 的概率在这个位置上

\(Code\)

#include<cstdio>
#include<cstring>
#define LL long long
using namespace std;

const int N = 2e3 + 5;
const LL P = 258280327;
LL f[N][N] , pow[N];

inline LL fpow(LL x , LL y)
{
	if (x == 0 && y == 0) return 0;
	x = (x + P) % P;
	LL res = 1;
	while (y)
	{
		if (y & 1) res = res * x % P;
		y >>= 1 , x = x * x % P;
	}
	return res;
}

int main()
{
	int T;
	scanf("%d" , &T);
	for(; T; T--)
	{
		int n; LL x , y , p;
		scanf("%d%lld%lld" , &n , &x , &y);
		p = x * fpow(y , P - 2) % P;
		pow[0] = 1;
		for(register int i = 1; i <= n; i++) pow[i] = pow[i - 1] * (1 - p + P) % P;
		memset(f , 0 , sizeof f);
		f[0][0] = 1;
		for(register int i = 1; i < n; i++)
		{
			f[i][0] = f[i - 1][0] * (1 - pow[0] + P) % P;
			for(register int j = 1; j < n; j++)
				f[i][j] = f[i - 1][j - 1] * pow[j - 1] % P ,
				f[i][j] += f[i - 1][j] * (1 - pow[j] + P) % P;
		}
		for(register int k = 0; k < n; k++)
		{
			LL ans = 0;
			for(register int i = 0; i < n; i++) ans = (ans + f[i][k]) % P;
			printf("%lld " , ans * pow[k] % P * fpow(n , P - 2) % P);
		}
		printf("\n");
	}
}