Neural Network模型复杂度之Residual Block - Python实现

• 背景介绍
  
  Neural Network之模型复杂度主要取决于优化参数个数与参数变化范围. 优化参数个数可手动调节, 参数变化范围可通过正则化技术加以限制. 本文从优化参数个数出发, 以Residual Block技术为例, 简要演示Residual Block残差块对Neural Network模型复杂度的影响.

• 算法特征
  
  ①. 对输入进行等维度变换; ②. 以加法连接前后变换扩大函数空间

• 算法推导
  
  典型残差块结构如下,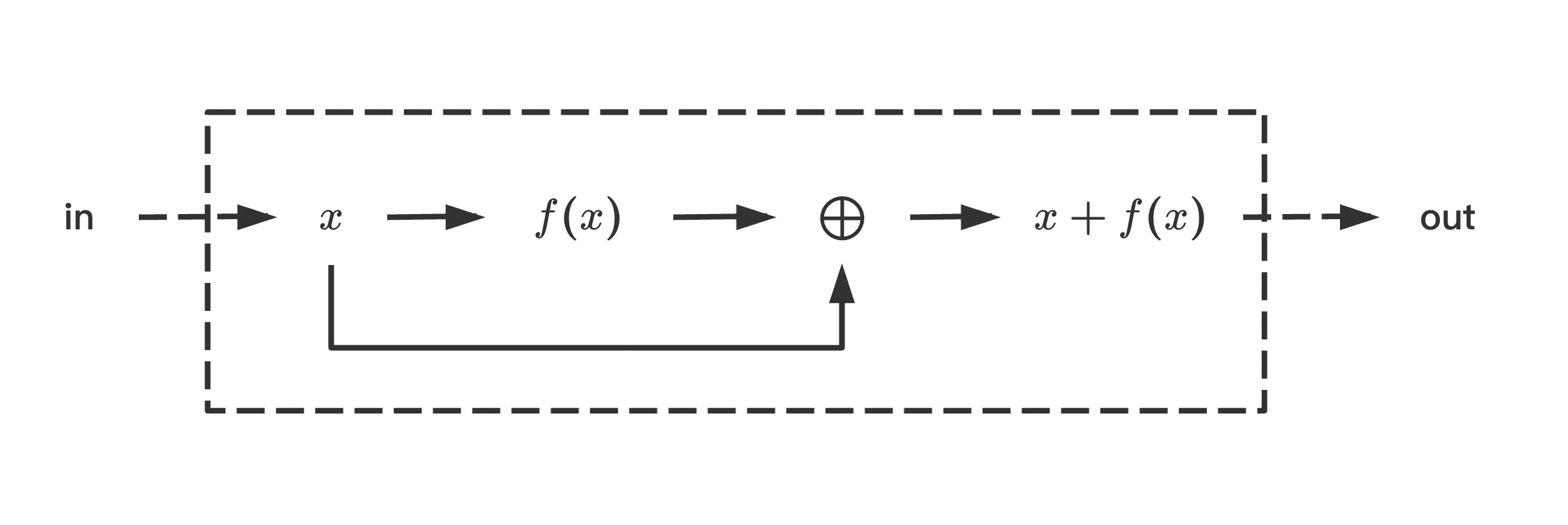

  

  即, 输入\(x\)之函数空间通过加法\(x + f(x)\)扩大. 可以看到, 在前向计算过程中, 函数\(f(x)\)之作用类似于残差, 补充输入\(x\)对标准输出描述之不足; 同时, 在反向传播过程中, 对输入\(x\)之梯度计算分裂在不同影响链路上, 降低了函数\(f(x)\)对梯度的直接影响.

• 数据、模型与损失函数
  
  数据生成策略如下,

  \[\left\{
  \begin{align*}
  x &= r + 2g + 3b \\
  y &= r^2 + 2g^2 + 3b^2 \\
  lv &= -3r - 4g - 5b
  \end{align*}
  \right.
  \]

  Neural Network网络模型如下,

  

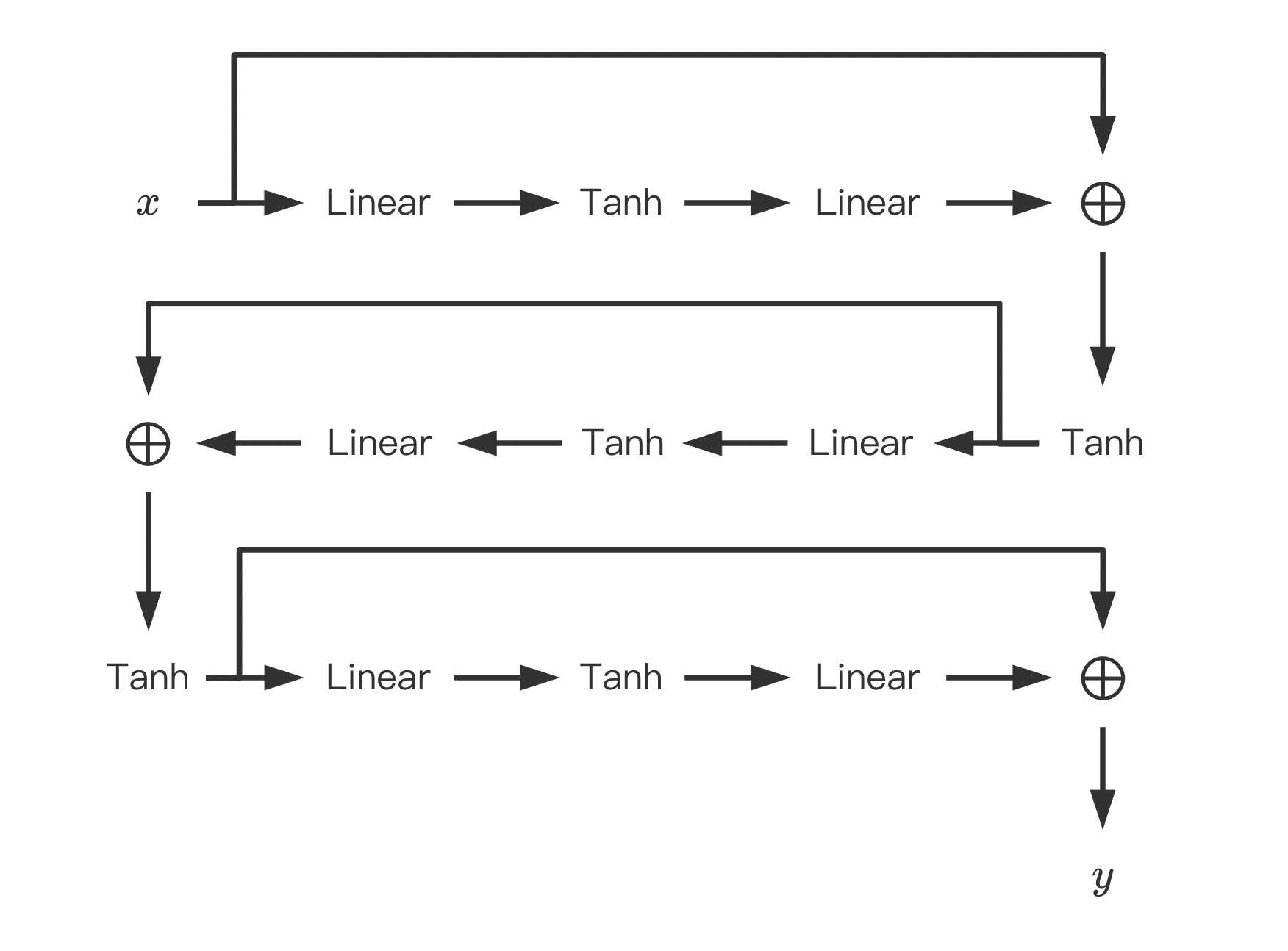
  其中, 输入层\(x:=(r, g, b)\), 输出层\(y:=(x, y, lv)\), 中间所有隐藏层与输入之dimension保持一致.
  
  损失函数如下,

  \[L = \sum_{i}\frac{1}{2}(\bar{x}^{(i)} - x^{(i)})^2 + \frac{1}{2}(\bar{y}^{(i)} - y^{(i)})^2 + \frac{1}{2}(\bar{lv}^{(i)} - lv^{(i)})^2
  \]

  其中, \(i\)为data序号, \((\bar{x}, \bar{y}, \bar{lv})\)为相应观测值.

• 代码实现
  
  本文以是否采用Residual Block为例(即在上述模型中是否去除\(\oplus\)), 观察Residual Block对模型复杂度的影响.

  code

  import numpy
  import torch
  from torch import nn
  from torch import optim
  from torch.utils import data
  from matplotlib import pyplot as plt
  
  numpy.random.seed(0)
  
  # 获取数据与封装数据
  def xFunc(r, g, b):
  	x = r + 2 * g + 3 * b
  	return x
  
  def yFunc(r, g, b):
  	y = r ** 2 + 2 * g ** 2 + 3 * b ** 2
  	return y
  
  def lvFunc(r, g, b):
  	lv = -3 * r - 4 * g - 5 * b
  	return lv
  
  class GeneDataset(data.Dataset):
  
  	def __init__(self, rRange=[-1, 1], gRange=[-1, 1], bRange=[-1, 1], \
  		num=100, transform=None, target_transform=None):
  		self.__rRange = rRange
  		self.__gRange = gRange
  		self.__bRange = bRange
  		self.__num = num
  		self.__transform = transform
  		self.__target_transform = target_transform
  
  		self.__X = self.__build_X()
  		self.__Y_ = self.__build_Y_()
  
  	def __build_Y_(self):
  		rArr = self.__X[:, 0:1]
  		gArr = self.__X[:, 1:2]
  		bArr = self.__X[:, 2:3]
  		xArr = xFunc(rArr, gArr, bArr)
  		yArr = yFunc(rArr, gArr, bArr)
  		lvArr = lvFunc(rArr, gArr, bArr)
  		Y_ = numpy.hstack((xArr, yArr, lvArr))
  		return Y_
  
  	def __build_X(self):
  		rArr = numpy.random.uniform(*self.__rRange, (self.__num, 1))
  		gArr = numpy.random.uniform(*self.__gRange, (self.__num, 1))
  		bArr = numpy.random.uniform(*self.__bRange, (self.__num, 1))
  		X = numpy.hstack((rArr, gArr, bArr))
  		return X
  
  	def __len__(self):
  		return self.__num
  
  	def __getitem__(self, idx):
  		x = self.__X[idx]
  		y_ = self.__Y_[idx]
  		if self.__transform:
  			x = self.__transform(x)
  		if self.__target_transform:
  			y_ = self.__target_transform(y_)
  		return x, y_
  
  # 构建模型
  class Model(nn.Module):
  
  	def __init__(self, is_residual_block=True):
  		super(Model, self).__init__()
  		torch.random.manual_seed(0)
  
  		self.__is_residual_block = is_residual_block
  		self.__in_features = 3
  		self.__out_features = 3
  
  		self.lin11 = nn.Linear(3, 3, dtype=torch.float64)
  		self.lin12 = nn.Linear(3, 3, dtype=torch.float64)
  		self.lin21 = nn.Linear(3, 3, dtype=torch.float64)
  		self.lin22 = nn.Linear(3, 3, dtype=torch.float64)
  		self.lin31 = nn.Linear(3, 3, dtype=torch.float64)
  		self.lin32 = nn.Linear(3, 3, dtype=torch.float64)
  
  	def forward(self, X):
  		X1 = self.lin12(torch.tanh(self.lin11(X)))
  		if self.__is_residual_block:
  			X1 += X
  		X1 = torch.tanh(X1)
  
  		X2 = self.lin22(torch.tanh(self.lin21(X1)))
  		if self.__is_residual_block:
  			X2 += X1
  		X2 = torch.tanh(X2)
  
  		X3 = self.lin32(torch.tanh(self.lin31(X2)))
  		if self.__is_residual_block:
  			X3 += X2
  		return X3
  
  # 构建损失函数
  class MSE(nn.Module):
  
  	def forward(self, Y, Y_):
  		loss = torch.sum((Y - Y_) ** 2)
  		return loss
  
  # 训练单元与测试单元
  def train_epoch(trainLoader, model, loss_fn, optimizer):
  	model.train(True)
  
  	loss = 0
  	with torch.enable_grad():
  		for X, Y_ in trainLoader:
  			optimizer.zero_grad()
  
  			Y = model(X)
  			lossVal = loss_fn(Y, Y_)
  			lossVal.backward()
  			optimizer.step()
  
  			loss += lossVal.item()
  
  	loss /= len(trainLoader.dataset)
  	return loss
  
  def test_epoch(testLoader, model, loss_fn, optimzier):
  	model.train(False)
  
  	loss = 0
  	with torch.no_grad():
  		for X, Y_ in testLoader:
  			Y = model(X)
  			lossVal = loss_fn(Y, Y_)
  			loss += lossVal.item()
  	loss /= len(testLoader.dataset)
  	return loss
  
  def train_model(trainLoader, testLoader, epochs=100):
  	model_RB = Model(True)
  	loss_RB = MSE()
  	optimizer_RB = optim.Adam(model_RB.parameters(), 0.001)
  
  	model_No = Model(False)
  	loss_No = MSE()
  	optimizer_No = optim.Adam(model_No.parameters(), 0.001)
  
  	trainLoss_RBList = list()
  	testLoss_RBList = list()
  	trainLoss_NoList = list()
  	testLoss_NoList = list()
  	for epoch in range(epochs):
  		trainLoss_RB = train_epoch(trainLoader, model_RB, loss_RB, optimizer_RB)
  		testLoss_RB = test_epoch(testLoader, model_RB, loss_RB, optimizer_RB)
  		trainLoss_No = train_epoch(trainLoader, model_No, loss_No, optimizer_No)
  		testLoss_No = test_epoch(testLoader, model_No, loss_No, optimizer_No)
  
  		trainLoss_RBList.append(trainLoss_RB)
  		testLoss_RBList.append(testLoss_RB)
  		trainLoss_NoList.append(trainLoss_No)
  		testLoss_NoList.append(testLoss_No)
  		if epoch % 50 == 0:
  			print(epoch, trainLoss_RB, trainLoss_No, testLoss_RB, testLoss_No)
  
  	fig = plt.figure(figsize=(5, 4))
  	ax1 = fig.add_subplot(1, 1, 1)
  	X = numpy.arange(1, epochs+1)
  	ax1.plot(X, trainLoss_RBList, "r-", lw=1, label="train with RB")
  	ax1.plot(X, testLoss_RBList, "r--", lw=1, label="test with RB")
  	ax1.plot(X, trainLoss_NoList, "b-", lw=1, label="train without RB")
  	ax1.plot(X, testLoss_NoList, "b--", lw=1, label="test without RB")
  	ax1.set(xlabel="epoch", ylabel="loss", yscale="log")
  	ax1.legend()
  	fig.tight_layout()
  	fig.savefig("loss.png", dpi=300)
  	plt.show()
  
  if __name__ == "__main__":
  	trainData = GeneDataset([-1, 1], [-1, 1], [-1, 1], num=1000, \
  		transform=torch.tensor, target_transform=torch.tensor)
  	testData = GeneDataset([-1, 1], [-1, 1], [-1, 1], num=300, \
  		transform=torch.tensor, target_transform=torch.tensor)
  	trainLoader = data.DataLoader(trainData, batch_size=len(trainData), shuffle=False)
  	testLoader = data.DataLoader(testData, batch_size=len(testData), shuffle=False)
  	epochs = 10000
  	train_model(trainLoader, testLoader, epochs)
  

• 结果展示

  

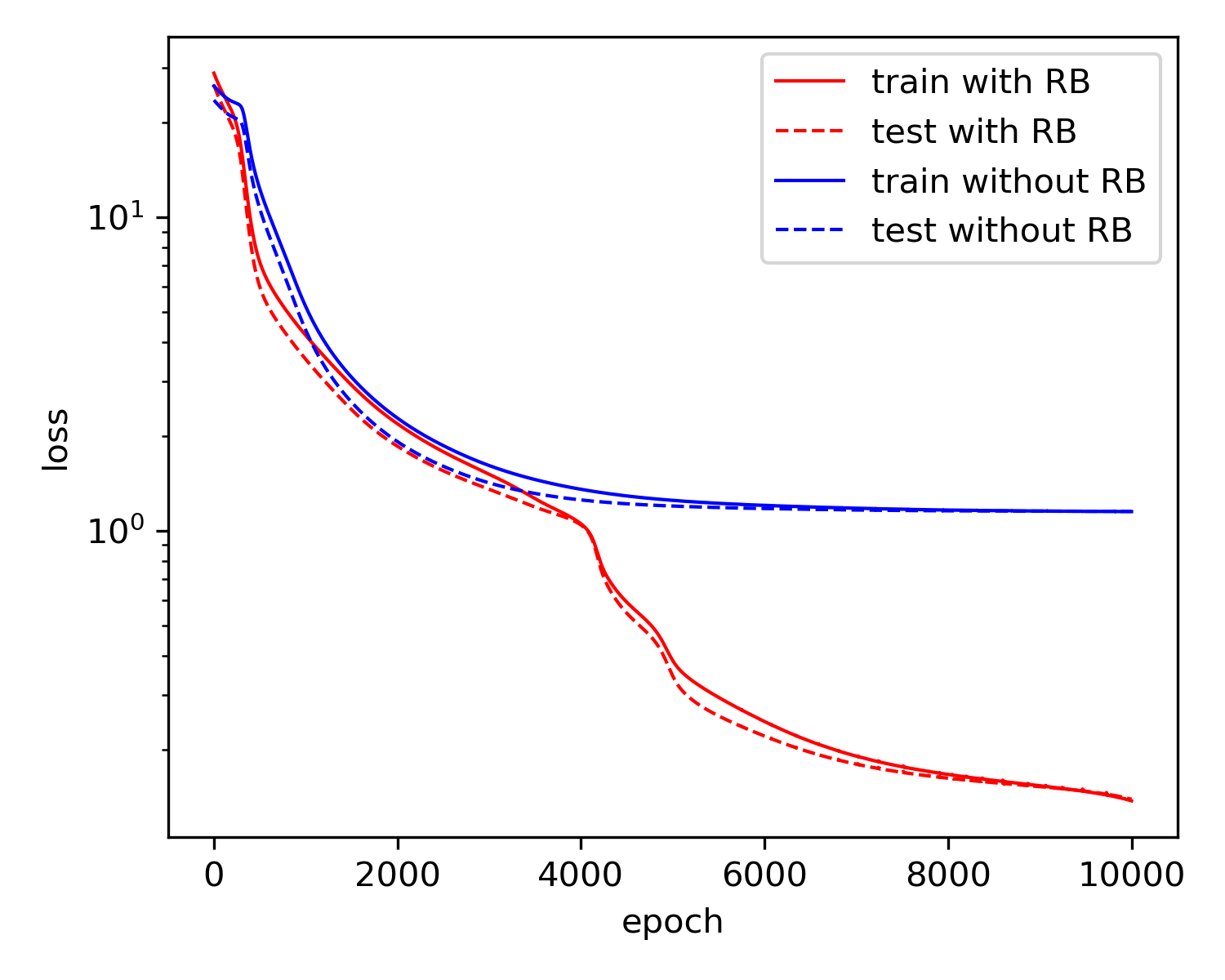
  可以看到, 由于Residual Block结构引入额外的优化参数, 模型复杂度得以提升. 同时, 相较于常规Neural Network(对应去除Residual Block之\(\oplus\)), Residual Block之Neural Network在优化参数个数相同的前提下更加稳妥地扩大了函数空间.

• 使用建议
  
  ①. 残差函数之设计应当具备与目标输出匹配之能力;
  
  ②. 残差函数之设计可改变dimension, 此时\(\oplus\)侧之输入应当进行线性等维调整;
  
  ③. 若训练数据之复杂度高于测试数据, 则在训练起始, 训练数据之loss可能也要高于测试数据.

• 参考文档
  
  ①. 动手学深度学习 - 李牧