leetcode5 最长回文字符串 动态规划 Manacher法

dp

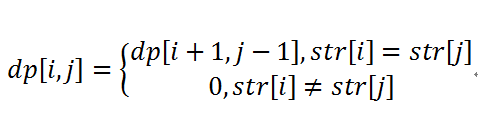
注意没有声明S不空，处理一下

o(n^2)

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.empty())
            return "";
        int len=s.length();
        int dp[len][len];
        for(int i=0;i<len;i++)
            for(int k=0;k<len;k++)
                dp[i][k]=0;
        int start=0,end=0;
        for (int i=0;i<len;i++)
        {
                dp[i][i]=1;
                if((i<len-1)&&(s[i]==s[i+1])){
                    dp[i][i+1]=1;
                    start=i;
                    end=i+1;
                }
        }
        for(int dis=2;dis<len;dis++)  //  i-> I-1,I+1，所以处理不了两个连续
        {
            for(int i=0;(i+dis)<len;i++)
                if((dp[i+1][i+dis-1]==1)&&(s[i]==s[i+dis]))
                {
                    dp[i][i+dis]=1;
                    if((dis)>(end-start)){
                        start=i;
                        end=i+dis;
                }
        }
        }
        return s.substr(start,end-start+1);
    }
};

遇到的问题:

== 写成了= 。。。。。

然后dp数组没有先mem为0...

然后是Manacher法

参考https://www.cnblogs.com/mini-coconut/p/9074315.html

首先，Manacher算法提供了一种巧妙地办法，将长度为奇数的回文串和长度为偶数的回文串一起考虑，

具体做法是，在原字符串的每个相邻两个字符中间插入一个分隔符，同时在首尾也要添加一个分隔符，分隔符的要求是不在原串中出现，一般情况下可以用#号。下面举一个例子：

（1）Len数组简介与性质

Manacher算法用一个辅助数组Len[i]表示以字符T[i]为中心的最长回文字串的最右字符到T[i]的长度，比如以T[i]为中心的最长回文字串是T[l,r],那么Len[i]=r-i+1。

对于上面的例子，可以得出Len[i]数组为:

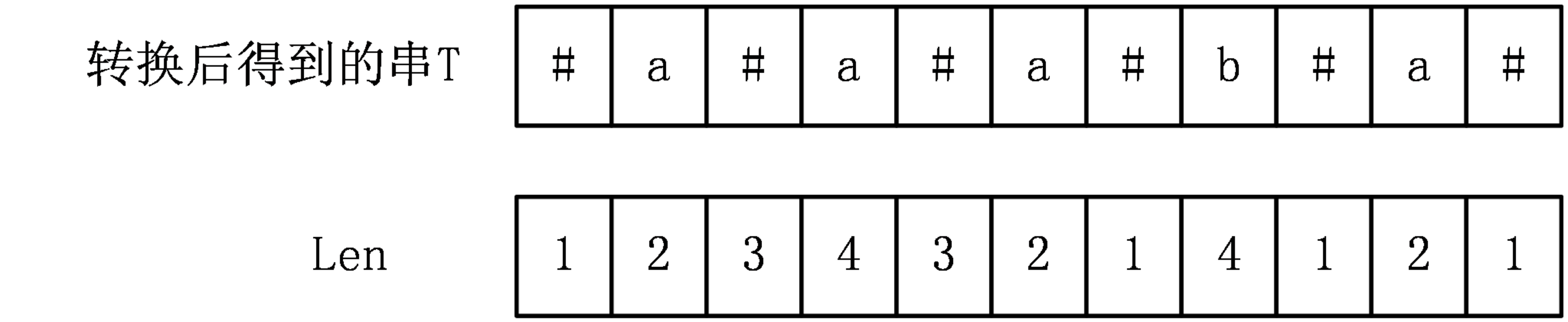
Len数组有一个性质，那就是Len[i]-1就是该回文子串在原字符串S中的长度，

证明，

首先在转换得到的字符串T中，所有的回文字串的长度都为奇数，那么对于以T[i]为中心的最长回文字串，其长度就为2*Len[i]-1,经过观察可知，T中所有的回文子串，其中分隔符的数量一定比其他字符的数量多1，也就是有Len[i]个分隔符，剩下Len[i]-1个字符来自原字符串，所以该回文串在原字符串中的长度就为Len[i]-1。

有了这个性质，那么原问题就转化为求所有的Len[i]。下面介绍如何在线性时间复杂度内求出所有的Len。

（2）Len数组的计算

首先从左往右依次计算Len[i]，当计算Len[i]时，Len[j](0<=j<i)已经计算完毕。

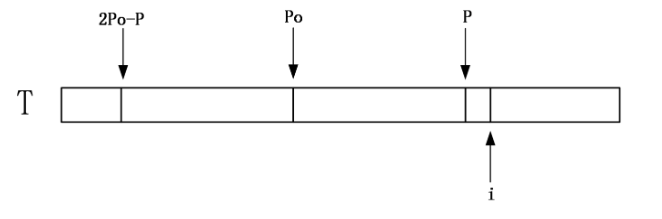
设P为之前计算中最长回文子串的右端点，并且设取得这个最大值的位置为po，分两种情况：

第一种情况：i<=P

那么找到i相对于po的对称位置，设为j，那么如果Len[j]<P-i，如下图：

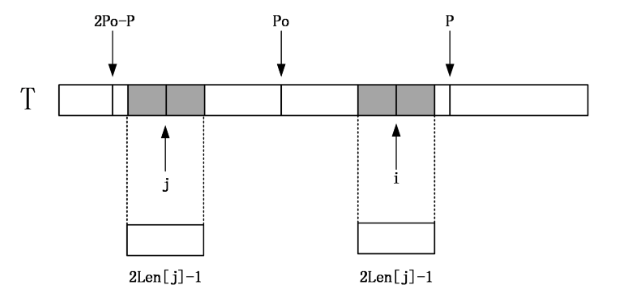
那么说明以j为中心的回文串一定在以po为中心的回文串的内部，且j和i关于位置po对称，

由回文串的定义可知，一个回文串反过来还是一个回文串，

所以以i为中心的回文串的长度至少和以j为中心的回文串一样（因为j，i及其附近点关于P对称，j所在回文串对称过去），即Len[i]>=Len[j]。

因为Len[j]<P-i,所以说i+Len[j]<P。由对称性可知Len[i]=Len[j]。

如果Len[j]>=P-i,由对称性，说明以i为中心的回文串可能会延伸到P之外，而大于P的部分我们还没有进行匹配，所以要从P+1位置开始一个一个进行匹配，直到发生失配，从而更新P和对应的po以及Len[i]。

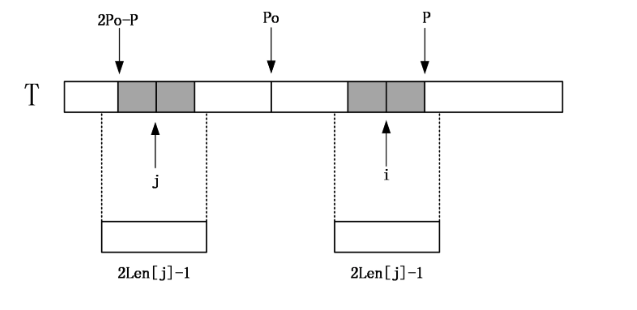
第二种情况: i>P

如果i比P还要大，说明对于中点为i的回文串还一点都没有匹配，这个时候，就只能老老实实地一个一个匹配了，匹配完成后要更新P的位置和对应的po以及Len[i]。

2.时间复杂度分析

Manacher算法的时间复杂度分析和Z算法类似，因为算法只有遇到还没有匹配的位置时才进行匹配，已经匹配过的位置不再进行匹配，所以对于T字符串中的每一个位置，只进行一次匹配，所以Manacher算法的总体时间复杂度为O(n)，其中n为T字符串的长度，由于T的长度事实上是S的两倍，所以时间复杂度依然是线性的。

下面是算法的实现，注意，为了避免更新P的时候导致越界，我们在字符串T的前增加一个特殊字符，比如说‘$’,所以算法中字符串是从1开始的。、

#include<iostream>

#include<limits.h>

#include<vector>

using namespace std;

#define max(a,b) (((a) > (b)) ? (a) : (b))

#define min(a,b) (((a) < (b)) ? (a) : (b))

class Solution {

public:

    string longestPalindrome(string s)

 {

    string manaStr = "$#";

    for (int i=0;i<s.size();i++) //首先构造出新的字符串

    {

      manaStr += s[i];

      manaStr += '#';

    }

    vector<int> rd(manaStr.size(), 0);//用一个辅助数组来记录最大的回文串长度，注意这里记录的是新串的长度，原串的长度要减去1

    int pos = 0, mx = 0;  //pos 当前最长回文串中点。mx当前最长回文串右端点

    int start = 0, maxLen = 0;  //起点，长度。  rd[i]即为上述len[i]

    for (int i = 1; i < manaStr.size(); i++) 

    {

      rd[i] = i < mx ? min(rd[2 * pos - i], mx - i) : 1;//越界 rd[2*pos-i 即为len[j]

      while (i+rd[i]<manaStr.size() && i-rd[i]>0 && manaStr[i + rd[i]] == manaStr[i - rd[i]])//这里要注意数组越界的判断

          rd[i]++;

      if (i + rd[i] > mx) //如果新计算的最右侧端点大于mx,则更新pos和mx

      {

        pos = i;

        mx = i + rd[i];

      }

      if (rd[i] - 1 > maxLen)

      {

        start = (i - rd[i]) / 2;

        maxLen = rd[i] - 1;

      }

    }

    return s.substr(start, maxLen);

  }

};

int main(int argc, char *argv[])

{

    string s="aacdefcaa";

    

    Solution solution;

    string ret = solution.longestPalindrome(s);

    cout<<ret<<endl;

    system("pause");

    return 0;

}