[Machine Learning] 多变量线性回归(Linear Regression with Multiple Variable)-特征缩放-正规方程

　　我们从上一篇博客中知道了关于单变量线性回归的相关问题，例如：什么是回归，什么是代价函数，什么是梯度下降法。

　　本节我们讲一下多变量线性回归。依然拿房价来举例，现在我们对房价模型增加更多的特征，例如房间数楼层等，构成一个含有多个变量的模型，模型中的特征为(x0 ,x1 ,...,xn )。

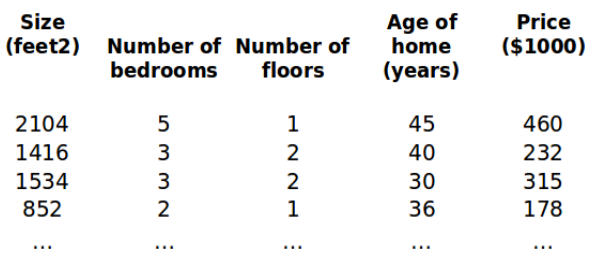
　　增添更多特征后，我们引入一系列新的注释：

　　假设函数 h 表示为:

　　这个公式中有 n+1个参数和 n 个变量，为了使得公式能够简化一些，引入x0 = 1，则公

式转化为: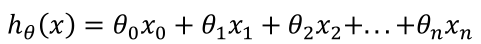

　　此时模型中的参数是一个 n+1维 的向量，任何一个训练实例也都是 n+1维的向量，特
征矩阵X的维度是m*(n+1)。因此公式可以简化为:。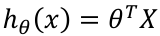

　　和单变量线性回归类似，在多变量线性回归中，构建一个代价函数，也是所有建模误差的平方和，即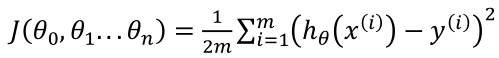：。其中。

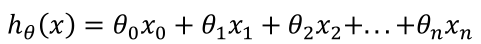　　使用梯度下降算法为:

　　代码示例：

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

　　在多变量中有个问题，就是每个变量的取值范围不是一样的，比如 一套房子的房间数量大概是 0-5, 而尺寸大约为 0-200平方米，如果以上述的两个取值范围代入代价函数进行计算的话，整个计算权重就会偏移，所以我们把所有变量的取值范围归一到 [-1,1]之间，那么 把变量的取值范围归一的步骤就叫 特征缩放。对于有些数据可能需要平方或者是三次方的操作，我们也可以归一化，把三次方去掉，从而转化为线性回归。特征缩放 可以加快梯度下降。

　　对于学习率，梯度下降算法的每次迭代受到学习率的影响，如果学习率