图论算法（二）最短路算法：Floyd算法！

最短路算法（一）

最短路算法有三种形态：Floyd算法，Shortset Path Fast Algorithm（SPFA）算法，Dijkstra算法。

我个人打算分三次把这三个算法介绍完。

（毕竟写太长了又没有人看QAQ……）但是这篇博客好像又双叒叕写的有点长，真的请各位耐心看完QAQ

今天先来介绍最简单的Floyd算法。

Part 1：最短路问题是什么？

我们用专业一点的术语表达，大概是这样子的：

若网络中的每条边都有一个数值（长度、成本、时间等），则找出两节点（通常是源节点和阱节点）之间总权和最小的路径就是最短路问题。

——摘自百度百科

但是完全不用关那些个专业的东西，我们通过字面意思大概就能Get到——求出某个点走到某个点之间的权值之和最小。

比如我们有一张图：

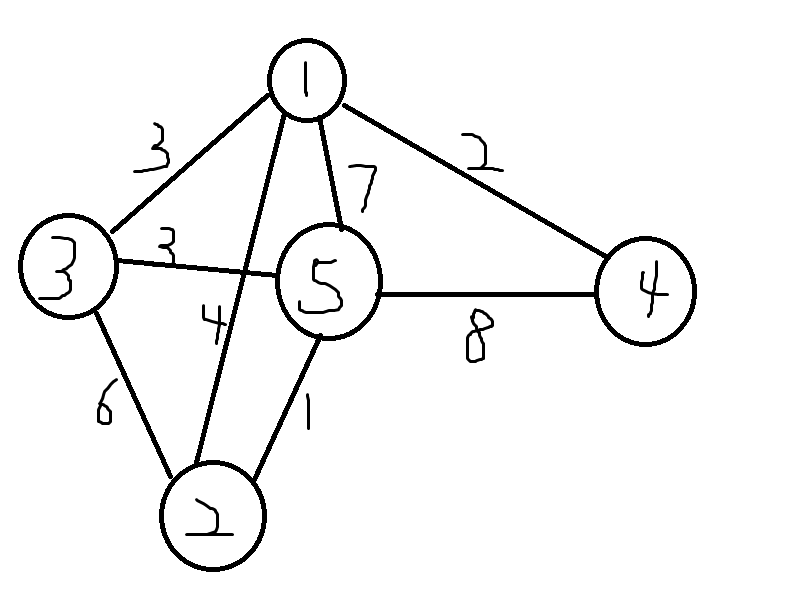
比如我们要求出从点1到点5的最短路就是这样的

点1->点2（走了4），点2->点5（走了1），这样点1到点5的最短距离就是5，（因为找不到比5更短的路可以从点1到点5）最短路就是1->4->5。

Part 2：Floyd算法思路

在介绍Floyd算法之前，我们先思考这样一个问题：

有一张图，我们要求出最短路。怎么做？

我们可以间接的把它看成一个DP来搞，那么状态就是这样的：

我们枚举点k，i，j，并假设i是起始点。

如果i->j的当前最短路长度 > i->k的最短路长度+k->j的最短路长度，我们就更新i->j的最短路长度是i->k+k->j。

什么意思呢？仔细思考一下，得出如下结果：

我们如果从某点直接到x点比先到y点再到x点的路径之和还要长的话，当然就要更新“某点”到x点的最短距离啦！

对于这个思想，科学家已经给出了证明，我这里不再赘述。

（以下是证明过程，反正我是看不懂，但是NOI又不考算法为什么对，其实我们只要知道算法的正确性和怎么应用就好了，至于证明，那是数学家的事情）

Part 3：Floyd算法的各项性能数据、适用范围、初始化注意事项

我们知道了Floyd算法的大致框架了，在康代码之前，还有一个不能忽略的问题：它的适用范围是什么。

（毕竟最短路有三种算法，算法竞赛的时候不一定考哪种，万一用错了算法……）

适用范围：存在负权边但是没有负权回路的有向图、无向图。（所有算法都不能解决负权回路，因为那样根本不存在最短路）

时间复杂度O（n^3）时间复杂度要特别注意，当有500个点的时候就已经很危险了。

空间复杂度O（n^2）邻接矩阵限制了空间复杂度不能再优化了。

结果调用方法：存在邻接矩阵里，其中f[i][j]表示i->j的最短路长度。

算法主体代码长度（不包括初始化等等）：150B。

整个求最短路代码长度：约600B（已经是最短路算法中最短的了）。

初始化注意事项：先把邻接矩阵初始化为0x3f，然后把所有f[i][i]初始化为0。

Part 4：Floyd算法结构框架

具体思路和注意事项我上面已经讲得很清楚了，我这里直接上模板代码。

#include<algorithm>
#include<cstring>
#include<cstdio>
#define N 1010
void floyd()
{
    for(int k=;k<=n;k++)//枚举中间点k(一定一定是在最外层循环！)
        for(int i=;i<=n;i++)
            for(int j=;j<=i;j++)
                dist[i][j]=max(dist[i][j],dist[i][k]+dist[k][j]);
                //如果更优，更新最优解
}
int main()
{
    memset(dist,0x3f,sizeof(dist));//memset初始化
    scanf("%d%d",&n,&m);//n点m边图
    for(int i=;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        dist[x][y]=z;
        dist[y][x]=z;//初始化无向图邻接矩阵
    }
    for(int i=;i<=n;i++)
        dist[i][i]=;//对角线重新赋值为0
    floyd();//调用Floyd解决最短路问题
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            printf("%d ",dist[i][j]);//输出所有i->j的最短路径
        }
        printf("\n");
    }
    return ;
}

Part 5：Floyd算法在实际问题中的应用

我在某洛谷上找到了这样两个题，很适合初学最短路算法的选手：

https://www.luogu.com.cn/problem/P2910

https://www.luogu.com.cn/problem/P1828

值得注意的是：这两个题目不一定要用Floyd算法来解决，但是我们今天拿这两个题简单说说Floyd的实现注意事项。

首先看第一个题：洛谷P2910

虽然有超链接，我还是把题目的图贴上来吧。

这个题目没有直白的说“求最短路”（可能是板子题最后的尊严）但是明眼人都看出来了，出题人把权值抽象成了“危险程度”，规定了几个节点是必须访问的，求从出发点经过这些必须访问的节点的最短路径长度。

读懂了题意之后，思考这样一个问题：我们要用什么算法做这个题（这很重要！再次重申，最短路算法有三个，我们要选出最能对付这个题，在AC的前提下找出写起来最简单的算法）

首先看空间复杂度：点的个数N<=100也就是说，满足邻接矩阵的空间复杂度和时间复杂度。

必须到达的点有M<=10000个，也就是说，我们要求10000次单源最短路，Floyd算法可以一次性求出一张图内任意两点间的最短路。

综上所述，这个题满足使用Floyd算法的要求，并且我们说过，Floyd算法是最好写的单源最短路算法（没有之一！！！）

具体思路简单BB一下，我们求出最短路之后，用存下“必须经过的点”的数组，把相邻元素的最短路一次次累加，最后就可以得到最终答案。

上AC代码：

//#include<guxinlin&sutang>
//GXL AK IOI
#include<algorithm>
#include<cstring>
#include<cstdio>
#define N 110
#define M 10010
#define sutang 0
using namespace std;
int v[N][N],vis[M],dis[N][N],n,m,ans;
void floyd()
{
    for(int k=;k<=n;k++)
        for(int i=;i<=n;i++)
            for(int j=;j<=n;j++)
                dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
int main()
{
    scanf("%d%d",&n,&m);
    memset(dis,0x3f,sizeof(dis));
    for(int i=;i<=m;i++)
        scanf("%d",&vis[i]);
    for(int i=;i<=n;i++)
    {
        dis[i][i]=;
        for(int j=;j<=n;j++)
        {
            scanf("%d",&v[i][j]);
            dis[i][j]=v[i][j];
        }
    }
    floyd();
    for(int i=;i<=m;i++)
        ans+=dis[vis[i-]][vis[i]];
    printf("%d",ans);
    return sutang;
}

下一个题目，洛谷P1828

先上题目截图：

一眼看过去，节点数P<=800，800^3=512000000（5亿一千二百万）这个复杂度已经很危险了，但是为什么我们用Floyd算法AC掉了这个题呢？

下面是重点部分了，另外，上面的题的正解是n次堆优化dijkstra算法或者n次SPFA算法。

Floyd灵魂剪枝算法

其实这个题我本来没有用Floyd算法做，（我是用的SPFA通过的评测）但是我看到题解去的大神们写了这样一篇题解，提到了Floyd灵魂剪枝。

我觉得是很有用的一个小技巧，而且实现起来非常简单。于是我就把这个小技巧分享给大家。

具体思路是：如果给出的图是无向边，我们用邻接矩阵存图的时候是把无向边当成两条相反、长度相等的有向边来存的，这就导致我们循环枚举的的时候，更新了两次这个无向边，浪费了宝贵的时间。所以当图是无向图的时候，我们只需要枚举一半的边，更新的时候一下子更新两条边的最短距离，就可以优化一半的复杂度。（但是这个复杂度还是很高，只是一个小技巧，不是大优化）

说完了剪枝策略，我们来说说这个题的具体思路：

首先，每个节点可能有多个牛，我们就需要把第i头牛在第j个牧场记下来。

其次，我们需要找出一个点，使其到这些有奶牛的点距离之和最小，确认是最短路算法。我们不知道哪个点距离和最小，所以我们需要把所有点到所有点的单源最短路求出来，然后枚举每一个点的距离之和，找出最小值。找出所有点的单源最短路，Floyd算法可以做到。加上我们的剪枝策略，再加上O2优化，Floyd算法可以在1000ms内给出结果。

#include<algorithm>
#include<cstring>
#include<cstdio>
#define IAKIOI 0
#define N 1010
using namespace std;
int cow[N],dist[N][N],n,m,q,ans=;
void floyd()
{
    for(int k=;k<=n;k++)
    {
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=i;j++)//枚举一半，剩下的手动更新
            {
                if(dist[i][j]>dist[i][k]+dist[k][j])
                {
                    dist[i][j]=dist[i][k]+dist[k][j];
                    dist[j][i]=dist[i][j];//手动更新另一条边
                }
            }
        }
    }
}
int main()
{
    memset(dist,0x3f,sizeof(dist));//初始化
    scanf("%d%d%d",&q,&n,&m);
    for(int i=;i<=q;i++)//记录第i头牛所在牧场是cow[i]
        scanf("%d",&cow[i]);
    for(int i=;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        dist[x][y]=z;//数据里没有重边，所以不用特判（其实是我忘了
        dist[y][x]=z;
    }
    for(int i=;i<=n;i++)//初始化
        dist[i][i]=;
    floyd();//调用Floyd解决问题
    for(int i=;i<=n;i++)
    {
        int qaq=;
        for(int j=;j<=q;j++)//枚举第i个点的
        {
            qaq+=dist[i][cow[j]];//累加第i个点的总路程
        }
        ans=min(ans,qaq);//如果比最优答案还优，更新他
    }
    printf("%d",ans);//输出答案
    return IAKIOI;
}

好了今天的最短路学习分享就到这里，喜欢的记得三连QAQ（卑微博主求关注）