2019牛客暑期多校训练营（第四场）D-triples I

>传送门<

题意：求最少需要多少个3的倍数按位或后可以得到数字a

思路：利用3的倍数对应的二进制数的性质来先选出一个x，然后根据数字a再配一个y出来

首先，我们都知道十进制中，任意一个数只要每一位相加的和能被3整除，那么这个数就能被3整除。

这是为什么？

因为十进制中每一个位都会10^k次方，那么仅仅是每一位%3的值都是余1，那么我们只要凑3个余1的，那么3就能被这个数整除。

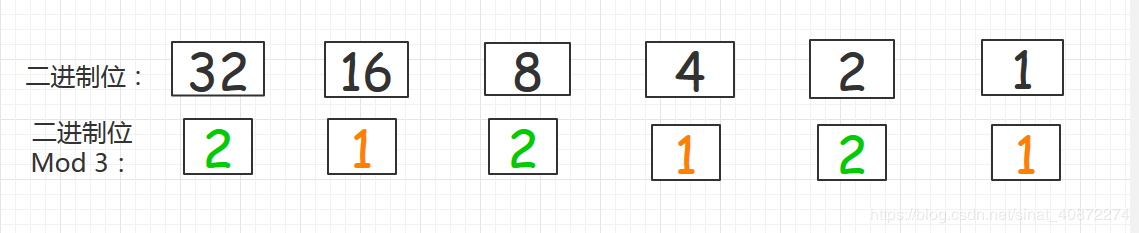
这题思路一样，换成2进制，只要各个位置上的数mod 3后的和相加起来mod 3为0，则这个数就是3的倍数

接下来分类讨论下：

A. 如果a是3的倍数，那么我们直接取a即可

B. 如果a的二进制只有一位或两位，我们根本取不出0以外的三的倍数，所以无解。题目保证有解所以可以基本不考虑太多。

C. a的二进制位至少有三位的情况
  首先明确一些性质
  1.每一个二进制位mod 3 只能得到 1 或 2
  2.每个mod 3 = 2 的数和 mod 3 = 1的数相加 一定是三的倍数
  3.mod 3 后余数相同的数相减以后一定也是三的倍数

Ⅰ. 若a mod 3 = 1

  如果a中的二进制位有至少两个mod 3 =1的，设它们为p和q，我们取{a-p,a-q}即可。
  因为a，p 和 q 都是mod 3 = 1的，所以a-p和a-q必定是三的倍数。同时a-p和a-q等于将原本p，q处的1变成了0. 这样一来，a-p和a-q按位或之后就还是a
  举个例子: a = 19

　　

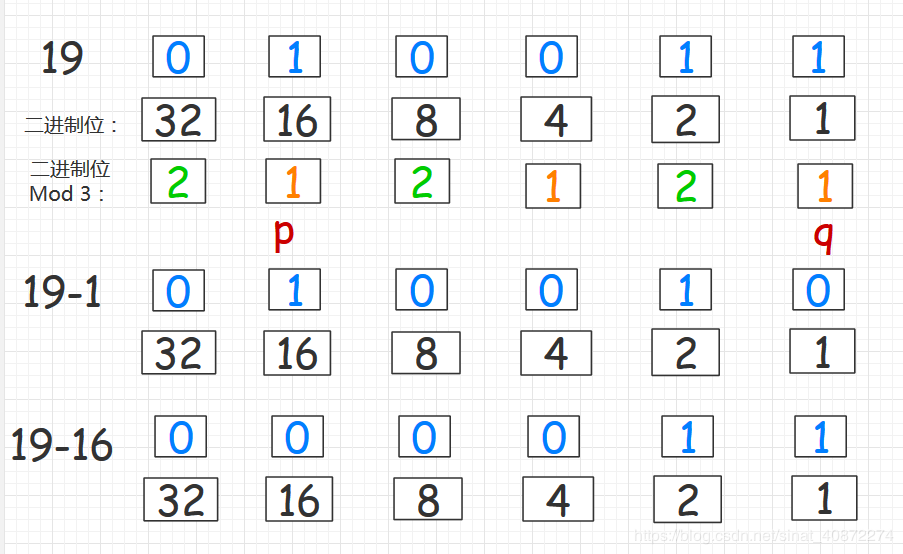
  如果a中的二进制位有恰好一个mod3=1的，那么设mod3=1的这个位为p，mod3=2的某个位为q，我们取{a-p,p+q}即可。
  a-p的道理同上，p+q 因为一个mod 3 = 1，一个 mod 3 = 2 所以两者加起来一定是三的倍数，同时p+q与a-p按位与一定是a，因为a-p去掉的p p+q给补上了 多出的q是原本a中就有的所以没有什么影响。

　　

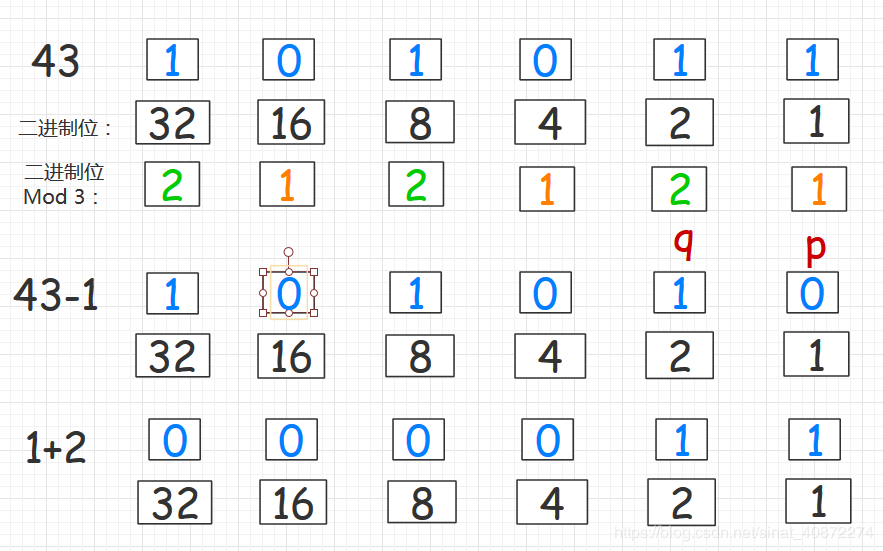
   如果a中的二进制位没有mod3=1的，那么假设有三个mod3=2的位p,q,r，我们取{a-p-q,p+q+r}即可。
   因为p和q都是mod 3 = 2，所以p+q mod 3 = 1，就和 a 是一样的了 故 a-p-q是三的倍数，又因为r也是 mod 3 = 2，所以q+p+r 原本是mod 3 = 6 ，6可以除尽3，所以q+p+r 也是三的倍数

　　

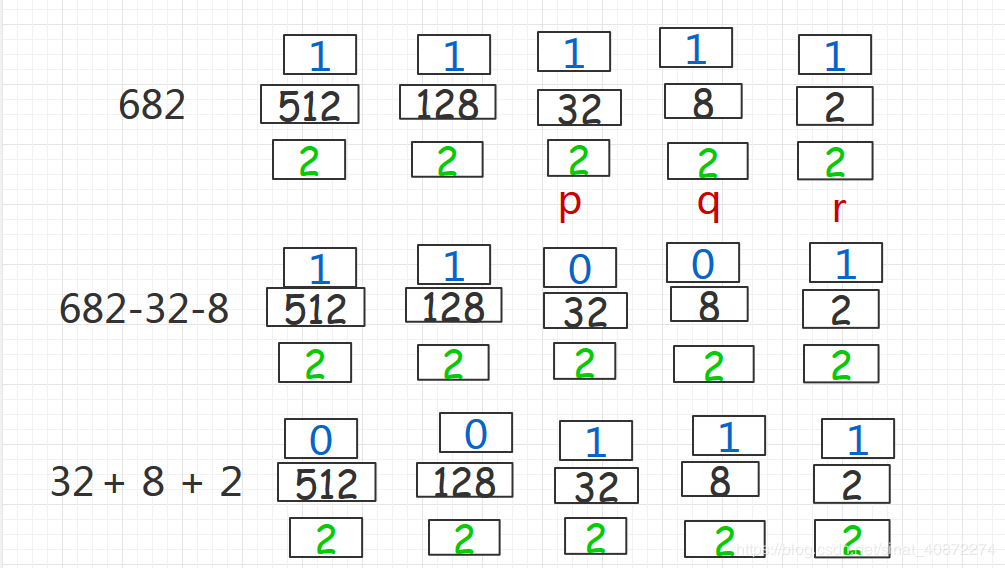
Ⅱ.若a mod 3 = 2

　　只需把上面的讨论中1与2互换即可，是完全对称的

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a;
void solve()
{
    scanf("%lld",&a);
    vector<ll> bb[2];
    for(int i=0;i<=60;i++)
    if((a>>i)&1) bb[i&1].push_back(1LL<<i); //记录每一个1的位置和保存他的奇偶
    if(a%3==0)
    printf("1 %lld\n",a);  //本身
    else if(bb[1].size()+bb[0].size()<=2)  return;//凑不出 (这里可能需要稍微仔细体会下)
    else{
        ll x,y;
        int s = (a%3==2); //余数是2还是1
        if(bb[s].size()){//如果原数里有我们需要的，可以直接减去的
            x = a-bb[s][0];
            if(bb[!s].size()) y = (bb[s][0]) + (bb[!s][0]); //凑3的两种方式
            else y = a - bb[s][1];
        }else{ //原数里没有余数
            x = a-(bb[!s][0]+bb[!s][1]);
            y =    bb[!s][0]+bb[!s][1]+bb[!s][2];
        }
        printf("2 %lld %lld\n",x,y);
    }
}
int main()
{
    int T; cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

---

参考自：
https://blog.csdn.net/sinat_40872274/article/details/97551579

https://blog.csdn.net/A_Pathfinder/article/details/97612078

（建议对着这两篇博客一起看）