【十天自制软渲染器】DAY 03：画一个三角形（向量叉乘算法 & 重心坐标算法）

如果你喜欢我写的文章，可以把我的公众号设为星标 ，这样每次有更新就可以及时推送给你啦。

前面两天画了点和线，今天我们来画一个最简单也是最强大的面——三角形。

本文主要讲解三角形绘制算法的推导和思路（只涉及到一点点的向量知识），最后会给出代码实现，大家放心的看下去就好。

本文源码 ：toyRenderer-day3-draw-triangle

1.如何画一个三角形？

在正式开始这一小节前，我们先想一下如何利用上一节的画线算法绘制一个实心的三角形。

假设现在平面内有三个不共线的点组成一个三角形，我们可以利用上一节的直线算法轻易的连接三角形的三条边，这时候我们会生成一个空心的、封闭的三角形。

那么这时候问题就转换为，如何把这个空心的三角形变为一个实心的三角形？

我想大家这时候已经有思路了，就是一行一行地扫描像素，把两个边界点之间的像素全部涂满上色就可以了。

day03_scanLineDrawTriangle

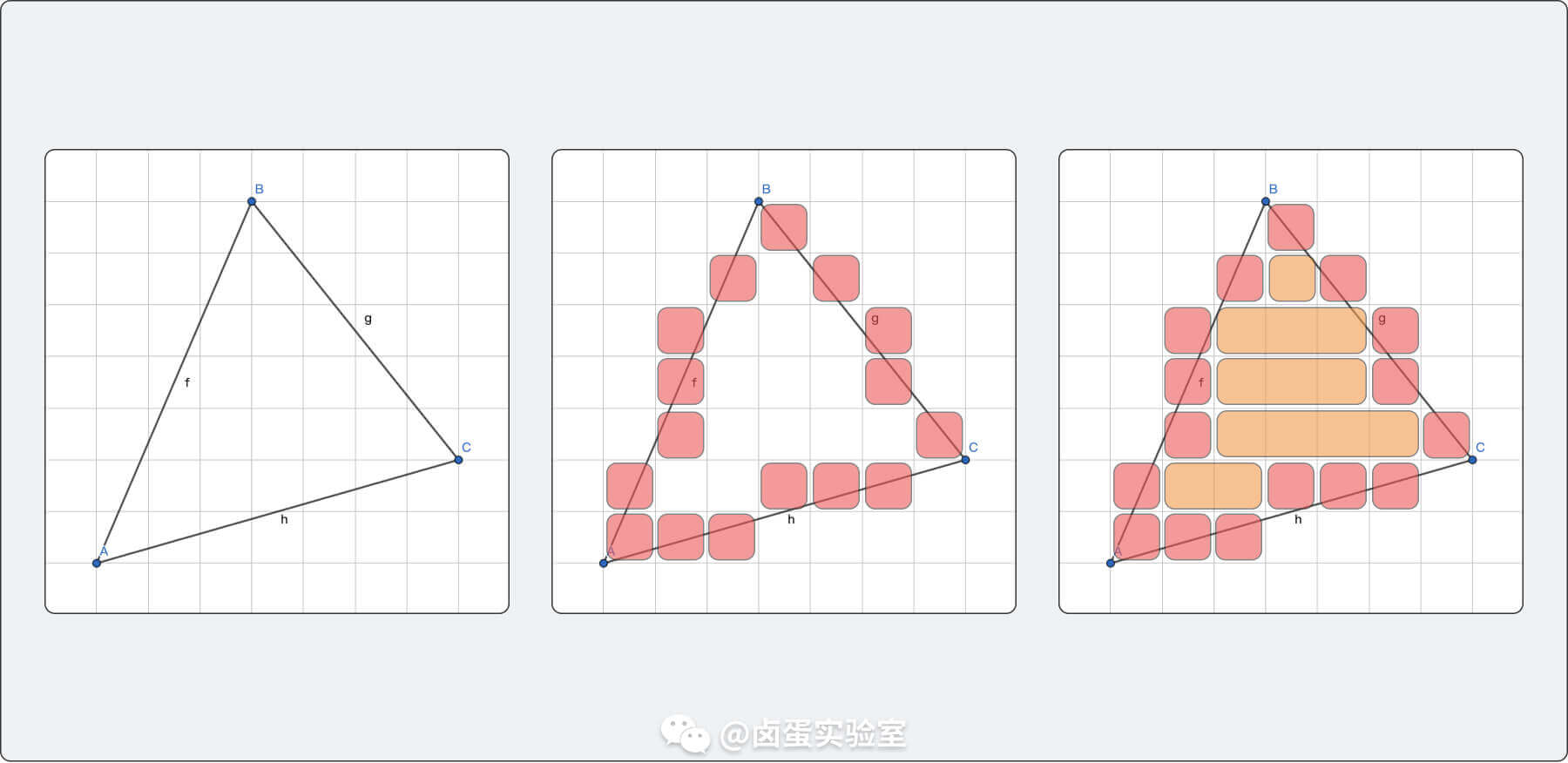
这个方法肯定是可以的，但是实现不是很优雅，也不是业内的主流实现方式。因为基于行扫描的算法不是本文的重点，所以详细的推导和代码实现就不提供了，感兴趣的同学可以自己尝试实现一下。

2.利用向量叉乘画三角形

开始本节前先简单复习一下向量叉乘的几何意义。

2.1 数学推导

在三维空间中，两个三维向量 和 做叉乘，会得到一个和已知两个向量垂直的新向量 。

既然叉乘产生的是一个新向量，那么它肯定有个方向，我们一般用右手定则来判断：将右手食指指向 的方向、中指指向 的方向，则此时拇指的方向即为 的方向。

右手定则

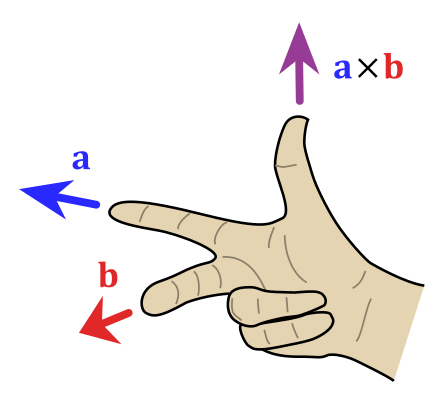
综上所述，我们可以对向量叉乘做一个严谨的定义：

其中 表示 和 在它们所定义的平面上的夹角（）。 和 是向量 和 的模长，而 则是一个与 、 所构成的平面垂直的单位向量，方向由右手定则决定。

有上面的理论，我们就可以判断两个向量的相对位置：

• 向量叉乘 向量，如果值为正，则表示 向量在 向量左侧
• 向量叉乘 向量，如果值为负，则表示 向量在 向量右侧
• 向量叉乘 向量，如果值为零，则表示 向量与 向量共线

会判断两条线的相对位置了，我们可以做个理论迁移，利用向量叉乘判断点和三角形的位置关系。

例如下面这里例子，对于三角形 来说，把三条边看作 、 、 三条首尾相连的向量，平面内有一个点 ，我们通过向量叉乘来判断相对位置：

day03_cross_product

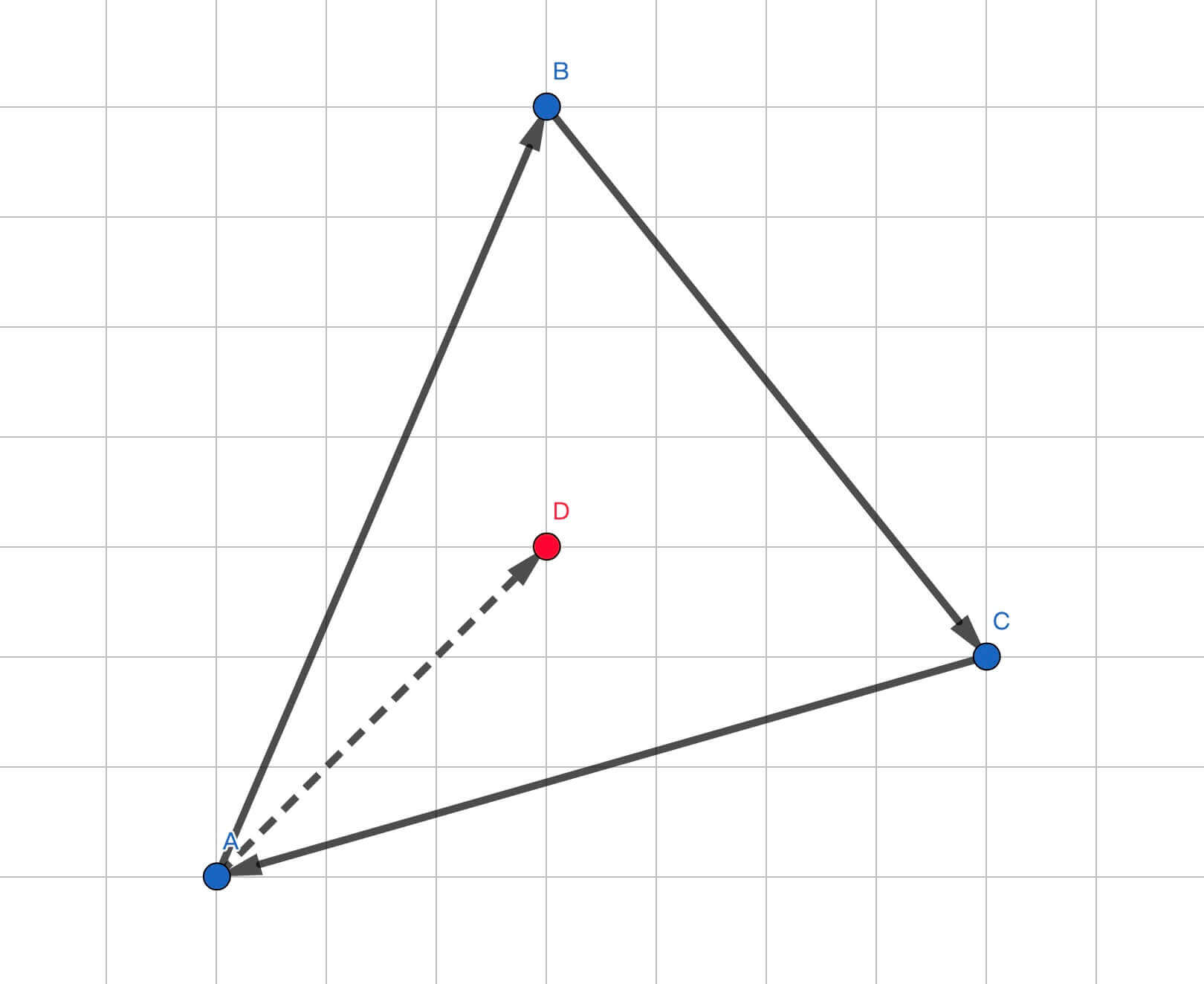
• ，值为正，故 在 左侧
• ，值为正，故 在 左侧
• ，值为正，故 在 左侧

综合以上三个限制条件，我们可以判断 在 内。

如果上面三个计算中有值为负的情况，说明 在三角形外；如果有值为 0 的情况，说明 在三角形的边或顶点上。

2.2 代码实现

理论基础复习完了，我们就可以写代码了。代码实现相当简单，我们构建一个函数 crossProduct，传入三角形的三个顶点和平面上的任意一点 ，然后根据四个顶点构建出向量计算叉乘就可以了：

// 利用叉乘判断是否在三角形内部
Vec3i crossProduct(Vec2i *pts, Vec2i P) {
    // 构建出三角形 ABC 三条边的向量
    Vec2i AB(pts[1].x - pts[0].x, pts[1].y - pts[0].y);
    Vec2i BC(pts[2].x - pts[1].x, pts[2].y - pts[1].y);
    Vec2i CA(pts[0].x - pts[2].x, pts[0].y - pts[2].y);
    
    // 三角形三个顶点和 P 链接形成的向量
    Vec2i AP(P.x - pts[0].x, P.y - pts[0].y);
    Vec2i BP(P.x - pts[1].x, P.y - pts[1].y);
    Vec2i CP(P.x - pts[2].x, P.y - pts[2].y);
    
    return Vec3i(AB^AP, BC^BP, CA^CP);
}

代码非常的简单，我们跑一个简单的例子验证一下：

void drawSingleTriangle() {
    // 图片的宽高
    int width  = 200;
    int height = 200;

    TGAImage frame(width, height, TGAImage::RGB);
    Vec2i pts[3] = {Vec2i(10, 10), Vec2i(150, 30), Vec2i(70, 160)};

    Vec2i P;
    // 遍历图片中的所有像素
    for (P.x = 0; P.x <= width - 1; P.x++) {
        for (P.y = 0; P.y <= height - 1; P.y++) {
            Vec3i bc_screen  = crossProduct(pts, P);

            // bc_screen 某个分量小于 0 则表示此点在三角形外（认为边也是三角形的一部分）
            if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) {
                continue;
            }
            
            image.set(P.x, P.y, color);
        }
    }
    
    frame.flip_vertically();
    frame.write_tga_file("output/day03_cross_product_triangle.tga");
}

看输出图像，我们已经成功绘制了一个三角形：

day03_cross_product_triangle

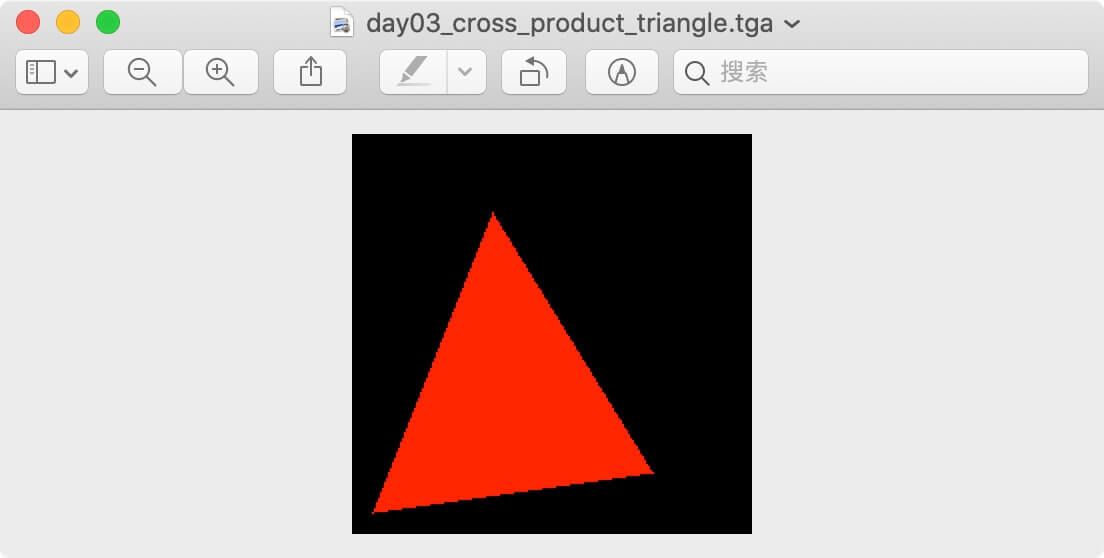
触不及防的安利：大家可以看我头像关注