第三十二篇 玩转数据结构——AVL树（AVL Tree）

 

 

 

1.. 平衡二叉树

• 平衡二叉树要求，对于任意一个节点，左子树和右子树的高度差不能超过1。
• 平衡二叉树的高度和节点数量之间的关系也是O(logn)
• 为二叉树标注节点高度并计算平衡因子
• 
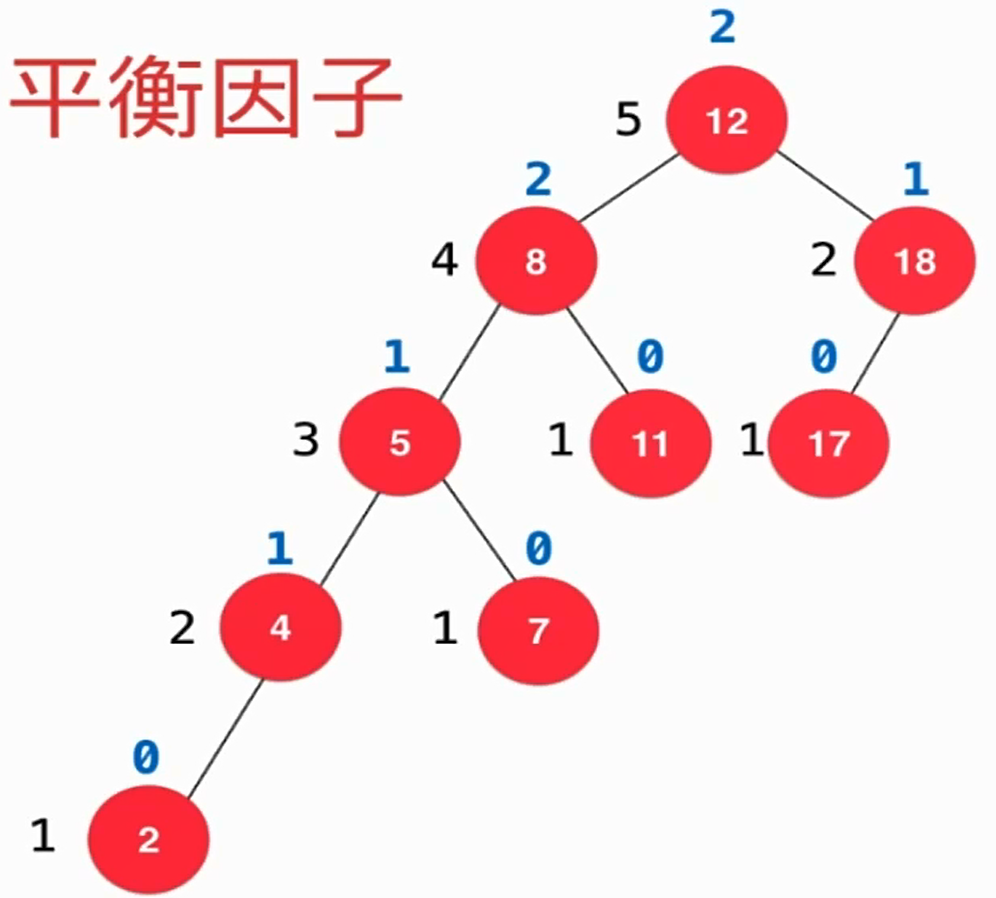
• AVL树是一棵平衡二叉树

2.. 实现AVL树的业务逻辑

• import java.util.ArrayList;
  
  public class AVLTree<K extends Comparable<K>, V> {
  
      private class Node {
          public K key;
          public V value;
          public Node left;
          public Node right;
          public int height;
  
          // 构造函数
          public Node(K key, V value) {
              this.key = key;
              this.value = value;
              left = null;
              right = null;
              height = 1;
          }
      }
  
      private Node root;
      private int size;
  
      // 构造函数
      public AVLTree() {
          root = null;
          size = 0;
      }
  
      // 实现getSize方法
      public int getSize() {
          return size;
      }
  
      // 实现isEmpty方法
      public boolean isEmpty() {
          return size == 0;
      }
  
      // 判断该二叉树是否为二分搜索树
      public boolean isBST() {
          ArrayList<K> keys = new ArrayList<>();
          inOrder(root, keys);
          for (int i = 1; i < keys.size(); i++) {
              if (keys.get(i - 1).compareTo(keys.get(i)) > 0) {
                  return false;
              }
          }
          return true;
      }
  
      private void inOrder(Node node, ArrayList<K> keys) {
  
          if (node == null) {
              return;
          }
          inOrder(node.left, keys);
          keys.add(node.key);
          inOrder(node.right, keys);
      }
  
      // 判断二叉树是否为平衡二叉树
      public boolean isBalanced() {
          return isBalanced(root);
      }
  
      // 判断以node为根的二叉树是否为平衡二叉树
      private boolean isBalanced(Node node) {
  
          if (node == null) {
              return true;
          }
          int balanceFactor = getBalanceFactor(node);
          if (Math.abs(balanceFactor) > 1) {
              return false;
          }
          return isBalanced(node.left) && isBalanced(node.right);
      }
  
      // 返回节点node的高度值
      private int getHeight(Node node) {
          if (node == null) {
              return 0;
          }
          return node.height;
      }
  
      // 返回节点node的平衡因子
      private int getBalanceFactor(Node node) {
          if (node == null) {
              return 0;
          }
          return getHeight(node.left) - getHeight(node.right);
      }
  
      // 对节点y进行向右旋转操作，返回旋转后新的根节点x
      //        y                              x
      //       / \                           /   \
      //      x   T4     向右旋转 (y)        z     y
      //     / \       - - - - - - - ->    / \   / \
      //    z   T3                       T1  T2 T3 T4
      //   / \
      // T1   T2
      private Node rightRotate(Node y) {
  
          Node x = y.left;
          Node T3 = x.right;
  
          // 向右旋转
          x.right = y;
          y.left = T3;
  
          // 更新height
          y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
          x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
  
          return x;
      }
  
      // 对节点y进行向左旋转操作，返回旋转后新的根节点x
      //    y                             x
      //  /  \                          /   \
      // T1   x      向左旋转 (y)       y     z
      //     / \   - - - - - - - ->   / \   / \
      //   T2  z                     T1 T2 T3 T4
      //      / \
      //     T3 T4
      private Node leftRotate(Node y) {
  
          Node x = y.right;
          Node T2 = x.left;
  
          // 向左旋转
          x.left = y;
          y.right = T2;
  
          //更新height
          y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
          x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
  
          return x;
      }
  
      // 实现add方法
      public void add(K key, V value) {
          root = add(root, key, value);
      }
  
      // 向以node为根节点的二分搜索树中插入元素(key, value)，递归算法
      // 返回插入新元素后的二分搜索树的根
      private Node add(Node node, K key, V value) {
  
          if (node == null) {
              size++;
              return new Node(key, value);
          }
  
          if (key.compareTo(node.key) < 0) {
              node.left = add(node.left, key, value);
          } else if (key.compareTo(node.key) > 0) {
              node.right = add(node.right, key, value);
          } else {
              node.value = value;
          }
  
          // 更新height值
          node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
  
          // 计算平衡因子
          int balanceFactor = getBalanceFactor(node);
  
          // 平衡维护
          // LL
          if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
              return rightRotate(node);
          }
          // RR
          if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
              return leftRotate(node);
          }
  
          // LR
          if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
              node.left = leftRotate(node.left);
              return rightRotate(node);
          }
          // RL
          if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
              node.right = rightRotate(node.right);
              return leftRotate(node);
          }
  
          return node;
      }
  
      // 返回以node为根节点的二分搜索树中，key所在的节点
      private Node getNode(Node node, K key) {
  
          if (node == null)
              return null;
  
          if (key.compareTo(node.key) < 0) {
              return getNode(node.left, key);
          } else if (key.compareTo(node.key) > 0) {
              return getNode(node.right, key);
          } else {
              return node;
          }
      }
  
      public boolean contains(K key) {
          return getNode(root, key) != null;
      }
  
      public V get(K key) {
  
          Node node = getNode(root, key);
          return node == null ? null : node.value;
      }
  
      public void set(K key, V newValue) {
          Node node = getNode(root, key);
          if (node == null)
              throw new IllegalArgumentException(key + " doesn't exist!");
  
          node.value = newValue;
      }
  
      // 返回以node为根的二分搜索树的最小元素所在节点
      private Node minimum(Node node) {
          if (node.left == null) {
              return node;
          }
          return minimum(node.left);
      }
  
      // 实现remove方法
      // 删除二分搜索树中键为key的节点
      public V remove(K key) {
          Node node = getNode(root, key);
  
          if (node != null) {
              root = remove(root, key);
              return node.value;
          }
          return null;
      }
  
      // 删除以node为根节点的二分搜索树中键为key的节点，递归算法
      // 返回删除节点后新的二分搜索树的根
      private Node remove(Node node, K key) {
          if (node == null) {
              return null;
          }
  
          Node retNode;
          if (key.compareTo(node.key) < 0) {
              node.left = remove(node.left, key);
              retNode = node;
          } else if (key.compareTo(node.key) > 0) {
              node.right = remove(node.right, key);
              retNode = node;
          } else {
              // 待删除节点左子树为空的情况
              if (node.left == null) {
                  Node rightNode = node.right;
                  node.right = null;
                  size--;
                  retNode = rightNode;
                  // 待删除节点右子树为空的情况
              } else if (node.right == null) {
                  Node leftNode = node.left;
                  node.left = null;
                  size--;
                  retNode = leftNode;
                  // 待删除节点左右子树均不为空
                  // 找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
                  // 用这个节点顶替待删除节点
              } else {
                  Node successor = minimum(node.right);
                  successor.right = remove(node.right, successor.key);  //这里进行了size--操作
                  successor.left = node.left;
                  node.left = null;
                  node.right = null;
                  retNode = successor;
              }
          }
  
          if (retNode == null) {
              return null;
          }
  
          // 更新height值
          retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
  
          // 计算平衡因子
          int balanceFactor = getBalanceFactor(retNode);
  
          // 平衡维护
          // LL
          if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
              return rightRotate(retNode);
          }
          // RR
          if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
              return leftRotate(retNode);
          }
  
          // LR
          if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
              node.left = leftRotate(retNode.left);
              return rightRotate(retNode);
          }
          // RL
          if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
              node.right = rightRotate(retNode.right);
              return leftRotate(retNode);
          }
  
          return retNode;
      }
  
      // 打印测试
      public static void main(String[] args) {
  
          System.out.println("Pride and Prejudice");
  
          ArrayList<String> words = new ArrayList<>();
  
          if (FileOperation.readFile("pride-and-prejudice.txt", words)) {
  
              System.out.println("Total words: " + words.size());
  
              AVLTree<String, Integer> map = new AVLTree<>();
              for (String word : words) {
                  if (map.contains(word)) {
                      map.set(word, map.get(word) + 1);
                  } else {
                      map.add(word, 1);
                  }
              }
  
              System.out.println("Total different words: " + map.getSize());
              System.out.println("Frequency of PRIDE: " + map.get("pride"));
              System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
  
              System.out.println("is BST: " + map.isBST());
  
              System.out.println("is Balanced: " + map.isBalanced());
          }
      }
  }