CodeForces-1234C-Pipes-dfs

You are given a system of pipes. It consists of two rows, each row consists of nn pipes. The top left pipe has the coordinates (1,1)(1,1) and the bottom right — (2,n)(2,n).

There are six types of pipes: two types of straight pipes and four types of curved pipes. Here are the examples of all six types:

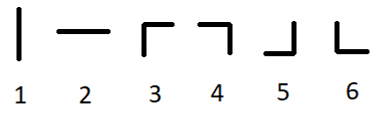Types of pipes

You can turn each of the given pipes 9090 degrees clockwise or counterclockwise arbitrary (possibly, zero) number of times (so the types 11 and 22 can become each other and types 3,4,5,63,4,5,6 can become each other).

You want to turn some pipes in a way that the water flow can start at (1,0)(1,0) (to the left of the top left pipe), move to the pipe at (1,1)(1,1), flow somehow by connected pipes to the pipe at (2,n)(2,n) and flow right to (2,n+1)(2,n+1).

Pipes are connected if they are adjacent in the system and their ends are connected. Here are examples of connected pipes:

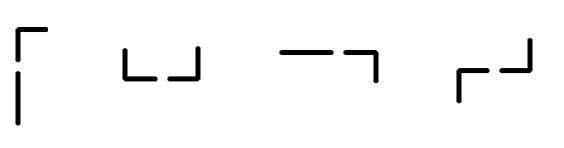Examples of connected pipes

Let's describe the problem using some example:

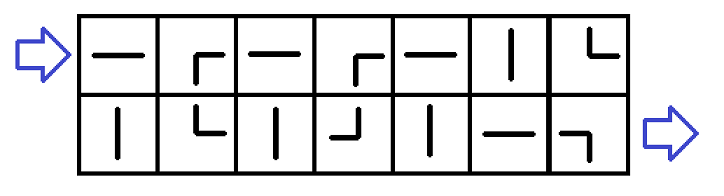The first example input

And its solution is below:

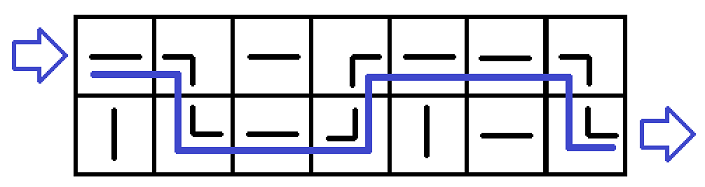The first example answer

As you can see, the water flow is the poorly drawn blue line. To obtain the answer, we need to turn the pipe at (1,2)(1,2) 9090 degrees clockwise, the pipe at (2,3)(2,3) 9090 degrees, the pipe at (1,6)(1,6) 9090 degrees, the pipe at (1,7)(1,7) 180180 degrees and the pipe at (2,7)(2,7) 180180degrees. Then the flow of water can reach (2,n+1)(2,n+1) from (1,0)(1,0).

You have to answer qq independent queries.

Input

The first line of the input contains one integer qq (1≤q≤1041≤q≤104) — the number of queries. Then qq queries follow.

Each query consists of exactly three lines. The first line of the query contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of pipes in each row. The next two lines contain a description of the first and the second rows correspondingly. Each row description consists of nndigits from 11 to 66 without any whitespaces between them, each digit corresponds to the type of pipe in the corresponding cell. See the problem statement to understand which digits correspond to which types of pipes.

It is guaranteed that the sum of nn over all queries does not exceed 2⋅1052⋅105.

Output

For the ii-th query print the answer for it — "YES" (without quotes) if it is possible to turn some pipes in a way that the water flow can reach (2,n+1)(2,n+1) from (1,0)(1,0), and "NO" otherwise.

input

6
7
2323216
1615124
1
3
4
2
13
24
2
12
34
3
536
345
2
46
54

output

YES
YES
YES
NO
YES
NO

Note

The first query from the example is described in the problem statement.

题意：

给出t组数据，每组数据给出两组长度为n的字符串，拼接起来代表一个长为n宽为2的长方形，水（0,0）进入，从右下角那个格子横着流出。若能从开头流出去，输出YES，否则输出NO。

水管有以下几种类型，可以90度旋转任意次，因为可以通过旋转得到，所以1、2可以看作是A类型，3-6可以看作是B类型。

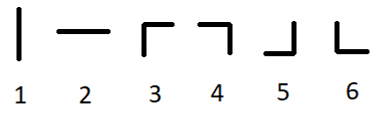
思路：

首先判断起点是什么类型的水管，进行dfs，自己定义四个方向（上下左右），开始进行dfs。dfs(x,y,ss)，x、y代表传入的下标，表示当前走到的点，ss表示当前的流向，然后再对当前流向所能到达的那个点

进行一下流向判断，判断其能流到哪里去。

 #include<stdio.h>
 #include<string.h>

 int flag,n;
 char a[][];

 //1左、2下、3右、4上

 void dfs(int x,int y,int ss)//从a[x][y]流过来，方向ss
 {
     if(y>=n)
         return;
     if(x==&&y==n-&&ss==)//x、y表示已经走到右下角了，ss=3表示是横着流出去的，符合题意
     {
         flag=;
         return;
     }
     if(x==)//从上一行流过来的,方向只能是向下或者向右
     {
         if(ss==)//判断的流过来的方向是怎么样的，向下流过来的
         {
             if(a[x+][y]!=''&&a[x+][y]!='')
                 dfs(x+,y,);
         }
         else if(ss==)//向右流过来的
         {
             if(a[x][y+]==''||a[x][y+]=='')
                 dfs(x,y+,);
             else dfs(x,y+,);
         }
     }
     else if(x==)//从下一行流过来的，方向只能是向上或者向右
     {
         if(ss==)//上
         {
             if(a[x-][y]!=''&&a[x-][y]!='')
                 dfs(x-,y,);
         }
         else if(ss==)//右
         {
             if(a[x][y+]==''||a[x][y+]=='')
                 dfs(x,y+,);
             else
                 dfs(x,y+,);
         }
     }
 }

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d",&n);
         scanf("%s %s",a[],a[]);
         flag=;
         if(a[][]==''||a[][]=='')//只能向右走
             dfs(,,);
         else//不然只能向下走
             dfs(,,);
         if(flag)
             printf("YES\n");
         else
             printf("NO\n");
     }
     return ;
 }