n的m划分 整数拆分问题

n的m划分

• 将n划分成若干个不超过m的数（正整数）的和，问有几种划分情况。

现在根据n和m的关系，考虑下面几种情况：

1. 当n=1时，不论m的值为多少，只有一种划分，即{1}；
2. 当m=1时，不论n的值为多少，只有一种划分，即{1,1,1,....1,1,1}划分成n个1；
3. 当n==m时，（a）划分中不包含n的情况，即n的n-1的划分f（n，n-1）；（b）其他情况就是包含n的划分，只有1个，即{n}；
4. 当n>=m时，（a）划分中不包含m的情况，即n的n-1划分f（n，m-1）；（b）其他情况就是包含m的划分，即{x1,x2,x3,x4,...,xi,m},也就是n-m的m划分f（n-m，m）；
5. 当n<m时，因为划分不会出现负数，因此也就是n的n划分。

综上的递推表达式为：

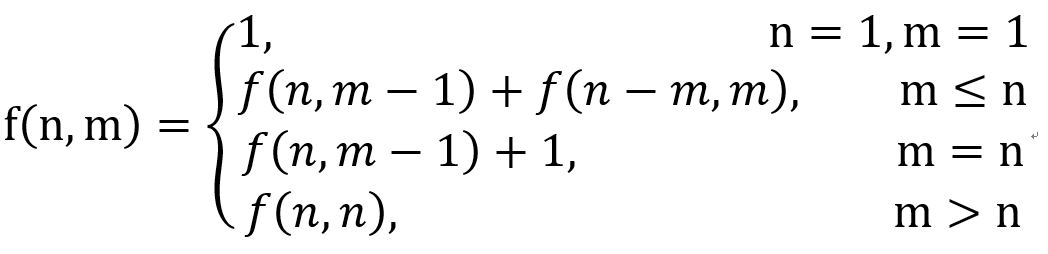
for(int i=; i<=n; i++)
    {
        for(int j=; j<=i; j++)
        {
            if(i==||j==) dp[i][j]=;
            else
            {
                if(j==i) dp[i][j]=dp[i][j-]+;
                else if((i-j)<j)
                    dp[i][j]=dp[i-j][i-j]+dp[i][j-];
                else
                    dp[i][j]=dp[i-j][j]+dp[i][j-];
            }
        }
    }

• 将n划分成不超过m个数（正整数）的和，问有几种情况。

dp[i][j]表示j的i划分。

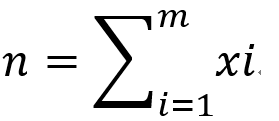
考虑n的m划分，如果对于每一个i都有xi>0，那么{xi-1}就对应了n-m的m划分。另外如果存在xi=0，那么就对应了n的m-1划分。

综上所述，对推关系：

dp[i][j]=dp[i][j-i]+dp[i-1][j]

dp[][]=;
    for(int i=;i<=m;i++)
    {
        for(int j=;j<=n;j++)
        {
            if((j-i)>=) dp[i][j]=(dp[i-][j]+dp[i][j-i])%mod;
            else dp[i][j]=dp[i-][j];
        }
    }