logistic回归和最大熵

回顾发现，李航的《统计学习方法》有些章节还没看完，为了记录，特意再水一文。

0 - logistic分布

如《统计学习方法》书上，设X是连续随机变量，X服从logistic分布是指X具有以下分布函数和密度函数：
\[F(x) = P(X \leq x)=\frac{1}{1+e^{-(x-\mu)/\gamma}}\]
\[f(x) = F'(x) = \frac{e^{-(x-\mu)/\gamma}}{1+e^{-(x-\mu)/\gamma}}\]
其中\(\mu\)是位置参数，\(\gamma\)是形状参数，logistic分布函数是一条S形曲线，该曲线以点\((\mu,\frac{1}{2})\)为中心对称，即：
\[F(-x+\mu)-\frac{1}{2} = -F(x-\mu)+\frac{1}{2}\]
\(\gamma\)参数越小，那么该曲线越往中间缩，则中心附近增长越快

图0.1 logistic 密度函数和分布函数

1 - 二项logistic回归

我们通常所说的逻辑回归就是这里的二项logistic回归，它有如下的式子：
\[h_\theta(\bf x)=g(\theta^T\bf x) = \frac{1}{1+e^{-\theta^T\bf x }}\]
这个函数叫做logistic函数，也被称为sigmoid函数，其中\(x_i\in{\bf R}^n,y_i\in\{0,1\}\)且有如下式子：
\(P(y=1|\bf x;\theta) = h_\theta(\bf x)\)
\(P(y=0|\bf x;\theta) =1- h_\theta(\bf x)\)
\(\log\frac{P(y=1|\bf x;\theta) }{1-P(y=1|\bf x;\theta) }=\theta^T\bf x\)
即紧凑的写法为：
\[p(y|\bf x; \theta) = (h_\theta(x))^y(1-h_\theta(\bf x))^{1-y}\]
基于\(m\)个训练样本，通过极大似然函数来求解该模型的参数：
\[\begin{eqnarray}L(\theta)
&=&\prod_{i=1}^mp(y^{(i)}|x^{(i)};\theta)\\
&=&\prod_{i=1}^m(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(\bf x^{(i)}))^{1-y^{(i)}}
\end{eqnarray}\]
将其转换成log最大似然：
\[\begin{eqnarray}\it l(\theta)
&=&\log L(\theta)\\
&=&\sum_{i=1}^my^{(i)}\log h(x^{(i)})+(1-y^{(i)})\log (1-h(x^{(i)}))
\end{eqnarray}\]
而该sigmoid函数的导数为：\(g'(z) = g(z)(1-g(z))\)，假设\(m=1\)（即随机梯度下降法）,将上述式子对关于\(\theta_j\)求导得：

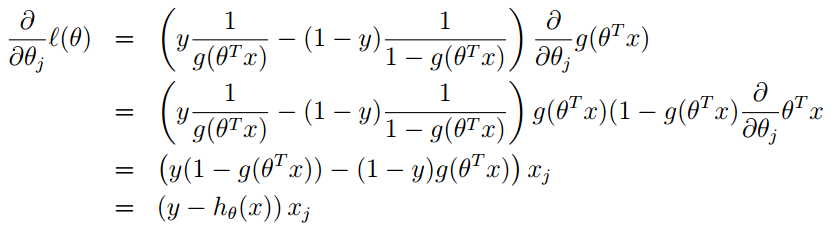
ps:上述式子是单样本下梯度更新过程，且基于第\(j\)个参数（标量）进行求导，即涉及到输入样本\(x\)的第\(j\)个元素\(x_j\)
而关于参数\(\theta\)的更新为：\(\theta:=\theta+\alpha\nabla_\theta\it l(\theta)\)
ps:上面式子是加号而不是减号，是因为这里是为了最大化，而不是最小化
通过多次迭代，使得模型收敛，并得到最后的模型参数。

2 - 多项logistic回归

假设离散型随机变量\(Y\)的取值集合为\({1,2,...,K}\)，那么多项logistic回归模型为：
\[P(Y=k|x) = \frac{e^{(\theta_k* \bf x)}}{1+\sum_{k=1}^{K-1}e^{(\theta_k* \bf x)}},k=1,2,...K-1\]
而第\(K\)个概率为：
\[P(Y=K|x) = \frac{1}{1+\sum_{k=1}^{K-1}e^{(\theta_k* \bf x)}}\]
这里\(x\in{\bf R}^{n+1},\theta_k\in {\bf R}^{n+1}\),即引入偏置。

3 - softmax

logistic回归模型的代价函数为：
\[J(\theta) = -\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)}\log h_\theta({\bf x}^{(i)})+(1-y^{(i)})\log (1-h_\theta({\bf x}^{(i)})) \right]\]
而softmax是当多分类问题，即\(y^{(i)}\in \{1,2,...,K\}\)。对于给定的样本向量\(\bf x\),模型对每个类别都会输出一个概率值\(p(y=j|\bf x)\)，则如下图：

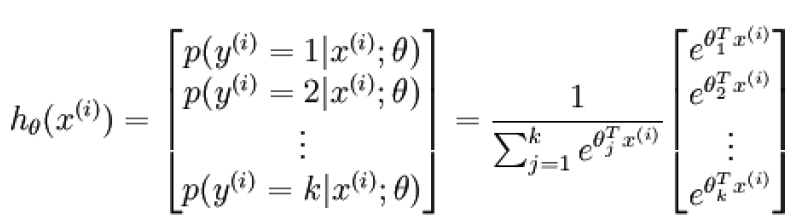
其中\(\theta_1,\theta_2,...\theta_k \in R^{n+1}\)都是模型的参数，其中分母是为了归一化使得所有概率之和为1.
从而softmax的代价函数为：
\[\begin{eqnarray}J(\theta)
&=& -\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{j=1}^K1\{y^{(i)}=j\}\log \frac{e^{\theta_j^T{\bf x}^{(i)}}}{\sum_{l=1}^Ke^{\theta_l^T{\bf x}^{(i)}}}\right]\\
&=& -\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{j=1}^K1\{y^{(i)}=j\}\left[\log {e^{\theta_j^T{\bf x}^{(i)}}}-\log{\sum_{l=1}^Ke^{\theta_l^T{\bf x}^{(i)}}}\right]\right]
\end{eqnarray}\]
其中，\(p(y^{(i)}=j|{\bf x}^{(i)};\theta)=\frac{e^{\theta_j^T{\bf x}^{(i)}}}{\sum_{l=1}^Ke^{\theta_l^T{\bf x}^{(i)}}}\)该代价函数关于第j个参数的导数为：
\[\begin{eqnarray}\nabla_{\theta_j}J(\theta)
&=&-\frac{1}{m}\sum_{i=1}^{m}1\{y^{(i)}=j\}\left[\frac{e^{\theta_j^T{\bf x}^{(i)}}* {\bf x}^{(i)}}{e^{\theta_j^T{\bf x}^{(i)}}}-\frac{e^{\theta_j^T{\bf x}^{(i)}}* {\bf x}^{(i)}}{\sum_{l=1}^Ke^{\theta_l^T{\bf x}^{(i)}}}\right]\\
&=&-\frac{1}{m}\sum_{i=1}^{m}1\{y^{(i)}=j\}\left[{\bf x}^{(i)}-\frac{e^{\theta_j^T{\bf x}^{(i)}}* {\bf x}^{(i)}}{\sum_{l=1}^Ke^{\theta_l^T{\bf x}^{(i)}}}\right]\\
&=&-\frac{1}{m}\sum_{i=1}^{m}{\bf x}^{(i)}\left(1\{y^{(i)}=j\}-\frac{e^{\theta_j^T{\bf x}^{(i)}}}{\sum_{l=1}^Ke^{\theta_l^T{\bf x}^{(i)}}}\right)\\
&=&-\frac{1}{m}\sum_{i=1}^{m}{\bf x}^{(i)}\left[1\{y^{(i)}=j\} - p(y^{(i)}=j|{\bf x}^{(i)};\theta)\right]
\end{eqnarray}\]
ps:因为在关于\(\theta_j\)求导的时候，其他非\(\theta_j\)引起的函数对该导数为0。所以\(\sum_{j=1}^K\)中省去了其他部分
ps:这里的\(\theta_j\)不同于逻辑回归部分，这里是一个向量;

4 - softmax与logistic的关系

将逻辑回归写成如下形式：
\[\begin{eqnarray}J(\theta)
&=& -\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)}\log h_\theta({\bf x}^{(i)})+(1-y^{(i)})\log (1-h_\theta({\bf x}^{(i)})) \right]\\
&=& -\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{j=0}^11\{y^{(i)}=j\}\log p(y^{(i)}=j|{\bf x}^{(i)};\theta)\right]
\end{eqnarray}\]
可以看出当k=2的时候，softmax就是逻辑回归模型

参考资料：
[] 李航，统计学习方法
[] 周志华，机器学习
[] CS229 Lecture notes Andrew Ng
[] ufldl
[] Foundations of Machine Learning