目录


这篇文章，看的晕晕的，但是被引用了400多次了，就简单地记一笔。


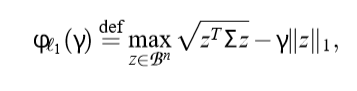
这个东西，因为\(\ell_1\)范数，所以会稀疏化，当然，和\(\gamma\)有关。

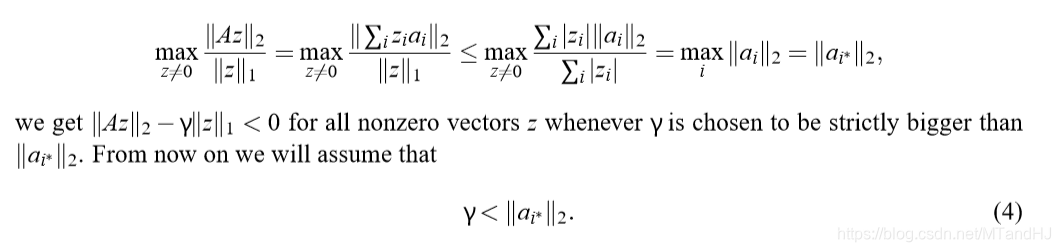
重点

我想重点写的地方是下面这个改写：

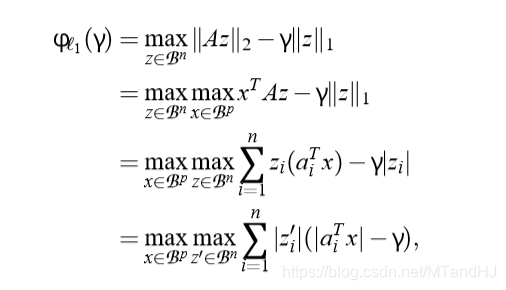
他们这些人都太会玩了。

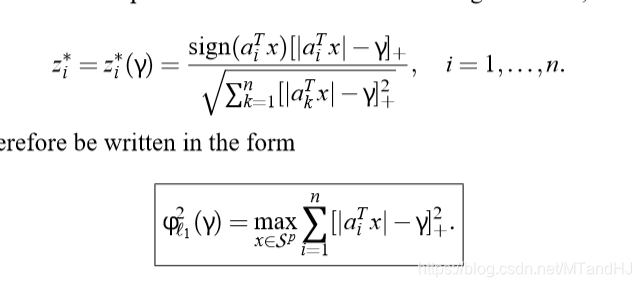
还有一些别的约束方法，比如\(\ell_0\)：

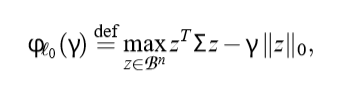
这个问题不知道该怎么求解，

接下来，把单一向量的求解扩展到了块求解，这里只做一个记号。

算法

Generalized Power Method for Sparse Principal Component Analysis的更多相关文章

  1. Sparse Principal Component Analysis via Rotation and Truncation

    目录 对以往一些SPCA算法复杂度的总结 Notation 论文概述 原始问题 问题的变种 算法 固定\(X\),计算\(R\) 固定\(R\),求解\(X\) (\(Z =VR^{\mathrm{T ...

  2. Sparse Principal Component Analysis

    目录 背景: 部分符号 创新点 文章梗概 The LASSO AND THE ELASTIC NET 将PCA改造为回归问题 定理二 单个向量(无需进行SVD版本) 定理三 多个向量(无需进行SVD, ...

  3. Full Regularization Path for Sparse Principal Component Analysis

    目录 背景 Notation Sparse PCA Semidefinite Relaxation Low Rank Optimization Sorting and Thresholding 背景 ...

  4. Sparse Principal Component Analysis via Regularized Low Rank Matrix Approximation(Adjusted Variance)

    目录 前言 文章概述 固定\(\widetilde{\mathrm{v}}\) 固定\(\widetilde{\mathrm{u}}\) Adjusted Variance 前言 这篇文章用的也是交替 ...

  5. 《principal component analysis based cataract grading and classification》学习笔记

    Abstract A cataract is lens opacification caused by protein denaturation which leads to a decrease i ...

  6. Principal Component Analysis(PCA) algorithm summary

    Principal Component Analysis(PCA) algorithm summary mean normalization(ensure every feature has sero ...

  7. Robust Principal Component Analysis?（PCP）

    目录 引 一些微弱的假设: 问题的解决 理论 去随机 Dual Certificates(对偶保证?) Golfing Scheme 数值实验 代码 Candes E J, Li X, Ma Y, e ...

  8. PCA（Principal Component Analysis）主成分分析

    PCA的数学原理(非常值得阅读)!!!!   PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可 ...

  9. Principal Component Analysis(PCA)

    Principal Component Analysis(PCA) 概念 去中心化(零均值化): 将输入的特征减去特征的均值, 相当于特征进行了平移, \[x_j - \bar x_j\] 归一化(标 ...

随机推荐

  1. [20190212]删除tab$记录的恢复3.txt

    [20190212]删除tab$记录的恢复3.txt --//春节前几天做了删除tan$记录的测试,链接:http://blog.itpub.net/267265/viewspace-2565245/ ...

  2. [20180926]查询相似索引.txt

    [20180926]查询相似索引.txt --//有时候在表上建立索引比如A,B字段,可能又建立B字段索引,甚至A字段索引以及B,A字段索引,或者还建立C,A字段索引,--//需要有1个脚本查询这些索 ...

  3. 语句调优基础知识-set statistics io on

    set statistics io on --清空缓存数据 dbcc dropcleanbuffers go --清空缓存计划 dbcc freeproccache go set statistics ...

  4. AndroidStudio2.2.x以上使用cMake编译调用底层c生成依赖库

    最近使用AndroidStudio的最新ndk编译方式cMake来编译底层cpp文件,由于之前没有接触过cMake语法,先附上官方学习文档地址:https://developer.android.co ...

  5. PHP中Snoopy类的使用

    最近看PHP书籍,发现了一个好东东,就是Snoopy类.Snoopy是一个php类库,用来模拟浏览器的功能,可以获取网页内容,发送表单. Snoopy的一些特点: 1抓取网页的内容 fetch 2 抓 ...

  6. LeetCode算法题-Pascal's Triangle（Java实现）

    这是悦乐书的第170次更新,第172篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第29题(顺位题号是118).给定非负整数numRows,生成Pascal三角形的第一个 ...

  7. Java strictfp

    strictfp关键字 用于强制Java中的浮点计算(float或double)的精度符合IEEE 754标准. 不使用strictfp:浮点精度取决于目标平台的硬件,即CPU的浮点处理能力. 使用s ...

  8. md5之守株待兔

    第一个实验吧的题目,不太会做,参考了很多大佬的经验,最后发现这个题目很简单,大概这就是入门的感觉吧!如果你多次尝试点开题目给的连接,就会发现,系统的密钥一直会变,可是我的密钥却保持一个,这就让我们联想 ...

  9. Python写代码的用法建议

    1.Mutable and immutable types Python有两种内置或用户定义的类型 可变类型是允许就地修改内容的类型.典型的可变列表是列表和词典:所有列表都有变异方法,如 list.a ...

  10. 【vue】vue +element 搭建项目，组件之间通信

    父子组件通信 父 通过props属性给 子传递数据 子 操作 父  this.$parent.XXX 子通过$emit传递参数 或者通过vue-bus vue-bus既可以实现父子组件之间的通信,也可 ...