Spring重温(一)--Spring快速入门

1.spring官网(https://repo.spring.io)下载依赖jar.

2.配置spring环境时还需要commons-logging相关jar。

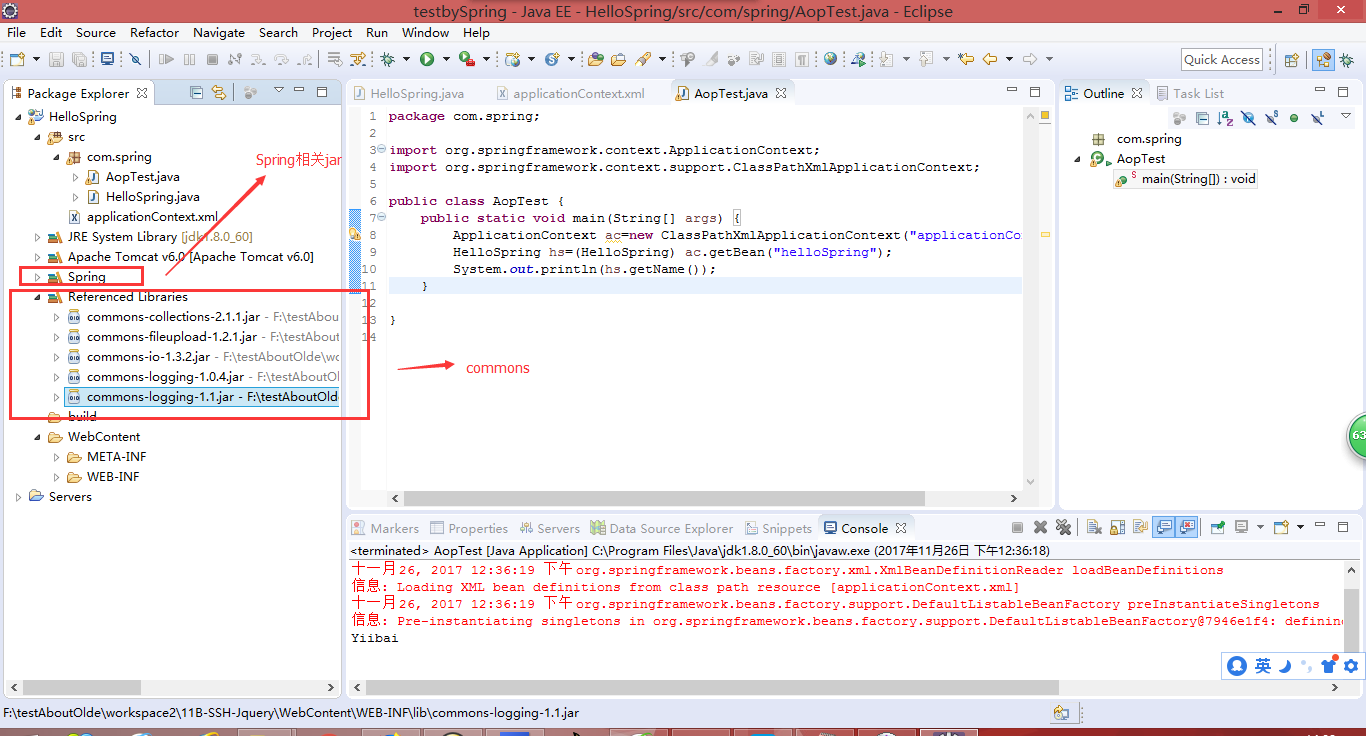
3.打开eclise创建一个工程，并将spring相关支持jar导入项目中，项目结构如下：

4.HelloSpring.java---一个简单的额Spring bean.

package com.spring;

public class HelloSpring {
  private String name;

public String getName() {
    return name;
}

public void setName(String name) {
    this.name = name;
}

}

5.aplicationContext.xml---Spring bean的配置文件。

<?xml version="1.0" encoding="UTF-8"?>
<beans
    xmlns="http://www.springframework.org/schema/beans"
    xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
    xmlns:p="http://www.springframework.org/schema/p"
    xsi:schemaLocation="http://www.springframework.org/schema/beans http://www.springframework.org/schema/beans/spring-beans-3.1.xsd">

    <bean id="helloSpring" class="com.spring.HelloSpring">
        <property name="name" value="Yiibai" />
    </bean>
</beans>

6.Aoptest.java---测试执行代码main方法。

package com.spring;

import org.springframework.context.ApplicationContext;
import org.springframework.context.support.ClassPathXmlApplicationContext;

public class AopTest {
    public static void main(String[] args) {
        ApplicationContext ac=new ClassPathXmlApplicationContext("applicationContext.xml");
        HelloSpring hs=(HelloSpring) ac.getBean("helloSpring");
        System.out.println(hs.getName());
    }

}

7.执行结果。

总结：IOC(Inversion of Control)控制反转--Ioc就是spring容器控制程序之间的关系,而非传统的程序代码直接控制，故，所谓控制反转即控制权由程序代码转移到外部容器中，这个控制权的转移即为反转。举个简单的例子：A类用到了B类的方法，此时，A类依赖于B类，那么我们在程序中需要在A类中new实例化B类，这是传统的程序代码控制；Spring 的Ioc表示A类中new实例化B类的权利，不是交给A类，而是交给Spring容器去实例化B对象，而Spring只需要在配置文件中配置类与类之间的依赖关系，告诉程序A用到了B。